Пример расчета шума ARC фильтра первого порядка
На рисунке 5.5 представлены электрическая схема ARC фильтра первого порядка и эквивалентная схема для расчета суммарного шума.
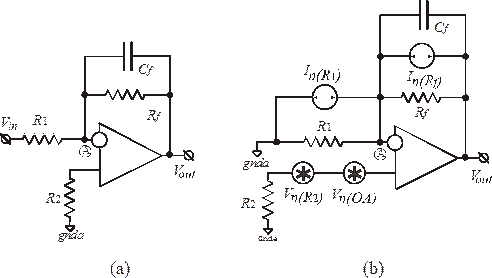
Рис. 5.5. ARC фильтр первого порядка: (а) электрическая схема;
(b) эквивалентная схема для расчета суммарного шума
Пусть для простоты ОУ имеет бесконечное усиление. Тогда передаточная функция фильтра при подаче входного сигнала как на Рис. 5.5.а, т.е. в цепь инвертирующего входа:
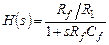 (5.22)
(5.22)
Передаточная функция фильтра при подаче входного сигнала на неинвертирующий вход:
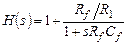 (5.23)
(5.23)
Теперь – о правомерности выбранных на Рис. 5.5.в эквивалентных схем шумящих резисторов. Как видно из рисунка, для R1 и Rf выбраны эквивалентные схемы с присоединенными параллельно источниками шумовых токов, а для R2 и для ОУ – присоединенный последовательно источник шумового напряжения. Проблема – в том, что последовательно присоединенный в любом месте источник напряжения как бы разделяет шумящий резистор какцелостную систему на части. Последнее в цепях со сквозным прохождением тока может привести к неправильной логике анализа и ошибкам.
Что касается источников шумовых токов, то, присоединенные параллельно, они не нарушают наглядной целостности и симметрии шумящего резистора, поэтому использование именно такого представления в любых цепях с протеканием постоянного тока предпочтительно и удобно. Однако, в цепях с отсутствием протекания постоянного тока, как на неинвертирующем входе КМДП ОУ с практически неопределенно высоким сопротивлением, корректно и достаточно удобно применять источники шумового напряжения.
Рассмотрим реакцию изображенной на Рис. 5.5.b схемы фильтра на шумовые источники (тока и напряжения) в отдельности (предполагая, что остальные равны нулю). Затем возведем полученные выходные напряжения в квадрат, сложим и получим суммарную спектральную плотность мощности шума на выходе 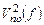 . Далее, для получения полной мощности шума
. Далее, для получения полной мощности шума 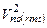 на выходе, производится интегрирование (в интересующих пределах) по частоте суммарной спектральной плотности шума
на выходе, производится интегрирование (в интересующих пределах) по частоте суммарной спектральной плотности шума 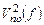 с учетом конкретных зависимостей спектральных плотностей шума от различных источников шума.
с учетом конкретных зависимостей спектральных плотностей шума от различных источников шума.
5.2.1. Реакция на шумовой источник тока 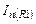
Отметим, что на обоих выводах резистора R1 – постоянные потенциалы, равные нулю, и ток через R1 равен нулю.
Уравнение Кирхгофа: 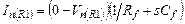 (5.24а)
(5.24а)
Получаем: 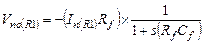 (5.24b)
(5.24b)
Спектральная плотность шума на выходе от шумового источника 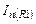 :
:
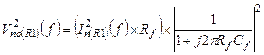 (5.25)
(5.25)
5.2.2. Реакция на шумовой источник тока 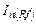
По-прежнему учитываем, что ток через R1 равен нулю.
Уравнение Кирхгофа: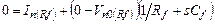 (5.26а)
(5.26а)
Получаем: 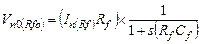 (5.26b)
(5.26b)
Спектральная плотность шума на выходе от шумового источника 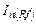 :
:
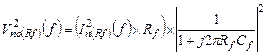 (5.27)
(5.27)
Как видно из (5.25) и (5.27), реакция на шумовой источник тока в цепи инвертирующего входа ОУ равна напряжению от протекания этого тока в резисторе в цепи обратной связи, умноженному на коэффициент передачи ARC фильтра без усиления.
5.2.3. Реакция на шумовой источник напряжения 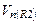
Базовая реакция сводится к тому, что все шумовое напряжение 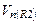 приложено к неинвертирующему входу ОУ. Поскольку, как условлено выше, ОУ является идеальным и имеет бесконечное усиление, потенциал на инвертирующем входе полностью повторяет потенциал неинвертирующего входа.
приложено к неинвертирующему входу ОУ. Поскольку, как условлено выше, ОУ является идеальным и имеет бесконечное усиление, потенциал на инвертирующем входе полностью повторяет потенциал неинвертирующего входа.
Спектральная плотность шума на выходе от шумового источника 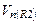 :
: 
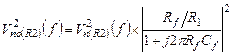 (5.28)
(5.28)
5.2.4. Реакция на приведенный ко входу источник напряжения
эквивалентного шума Операционного Усилителя 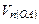
Удобнее всего такой источник напряжения разместить на неинвертирующем входе. Анализ аналогичен анализу реакции от резистора R2, поэтому и результат также аналогичен:
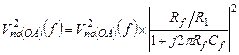 (5.29)
(5.29)
Полная мощность шума на выходе фильтра равна интегралу по частоте суммы спектральных плотностей шума от всех источников шума:
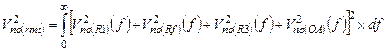 (5.30)
(5.30)
5.3. Пример расчета приведенного ко входу шума КМДП дифференциального
каскада с активной нагрузкой
На рис. 5.6 изображен КМДП дифференциальный каскад с активной нагрузкой. В цепь затвора каждого транзистора включен воображаемый эквивалентный источник приведенного к затвору шумового напряжения.
Пусть источник режимного тока на М0 по умолчанию имеет большое выходное сопротивление. Это дает возможность считать, что, например, увеличение шумового тока в М1 на какую-либо величину, влечет уменьшение тока в М2 на такую же величину. Пусть упомянутое увеличение тока в М1 обязано собственному шуму М1. Таким образом, полный шумовой ток транзистора М1 поделен пополам между М1 и М2. Аналогично происходит и с шумовым током М2, т.е половина его течет в М2 и половина – в М1.

Рис.5.6. КМДП
дифференциальный
каскад с активной
нагрузкой и с
приведенными
ко входам источниками
шума.
Рассмотрим транзисторы М3 и M4. Как для М3, так и для М4, потенциалы истоков неизменны, поэтому собственные шумовые токи в них текут полностью. Однако, отметим, что M3 включен как диод, поэтому изменение тока в M3, обязанное шуму, влечет изменение превышения над порогом 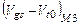 и, следовательно, потенциала узла А. Дополнительно в транзисторе M3 протекает ток, в том числе и шумовой, транзистора M1 и, следовательно, половин шумовых токов транзисторов M1 и M2. Все перечисленные выше шумовые токи (шумовой ток M3 и половинки шумовых токов M1 и M2) модулируют потенциал узла А. Но с узлом А соединен затвор транзистора M4, и этот транзистор становится источником перечисленных выше в скобках токов, но – противоположного знака. Однако, из последнего следует, что «отраженные» в M4 половинки шумовых токов M1 и M2, протекающие в M3, находятся в фазе с теми половинками шумовых токов M1 и M2, которые протекали в M2. Шумовой ток M3 полностью «отражается» в M4, а «собственный» для M4 шумовой ток в нем протекает всегда.
и, следовательно, потенциала узла А. Дополнительно в транзисторе M3 протекает ток, в том числе и шумовой, транзистора M1 и, следовательно, половин шумовых токов транзисторов M1 и M2. Все перечисленные выше шумовые токи (шумовой ток M3 и половинки шумовых токов M1 и M2) модулируют потенциал узла А. Но с узлом А соединен затвор транзистора M4, и этот транзистор становится источником перечисленных выше в скобках токов, но – противоположного знака. Однако, из последнего следует, что «отраженные» в M4 половинки шумовых токов M1 и M2, протекающие в M3, находятся в фазе с теми половинками шумовых токов M1 и M2, которые протекали в M2. Шумовой ток M3 полностью «отражается» в M4, а «собственный» для M4 шумовой ток в нем протекает всегда.
Итак, в M4, а, следовательно, и в M2, и в выходной цепи дифкаскада, протекаютполныешумовые токи четырех транзисторов: M1 – M4, и их квадраты арифметически складываются. Разумеется, совпадение фаз «первоначально» находившихся в M2 половинок шумовых токов M1 и M2 и «отраженных» половинок этих же токов возможно только в области относительнонизкихчастот, когда можно пренебречь задержкой фазы из-за паразитных емкостей в узлах А и В.
Рассмотрим теперь шум, вызываемый в выходной цепи транзистором M0.
В идеальном дифкаскаде (сейчас рассматривается именно этот случай) в обоих его симметричных ветвях текутполовинкисинфазного шумового тока транзистора M0 и вызывают изменения потенциалов в узлах А и out. Одинаковые токи в ветвях вызываютодинаковыеже потенциалы в этих узлах. Несмотря на высокое выходное сопротивление в узле out, при идентичностисинфазныхтоков, протекающих через узлы А и out, тем не менее, изменение потенциала затвора транзистора M4 определяетсяименно потенциалом узла А, т.е. изменение потенциала в узле А задаетпотенциал на выходе дифкаскада.
Итак,синфазныйток (в рассматриваемом случае являющийся шумовым током транзистора-генератора режимного тока) вызываетименно такоеизменение 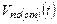 выходного потенциала,какоеопределяетсянизкимвыходным сопротивлением диода на транзисторе M3. Такую ситуацию также можно объяснитьполнойкорреляцией токов через узлы А и out.Дифференциальныйже ток от любого из четырех транзисторов M1 – M4, а также от суммы всех токов, вызывает изменение
выходного потенциала,какоеопределяетсянизкимвыходным сопротивлением диода на транзисторе M3. Такую ситуацию также можно объяснитьполнойкорреляцией токов через узлы А и out.Дифференциальныйже ток от любого из четырех транзисторов M1 – M4, а также от суммы всех токов, вызывает изменение 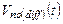 потенциала узла out, определяемоевысокимвыходным сопротивлением этого узла. Отношение дифференциального шумового напряжения
потенциала узла out, определяемоевысокимвыходным сопротивлением этого узла. Отношение дифференциального шумового напряжения 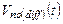 к синфазному
к синфазному 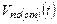 равно отношению выходных сопротивлений в узлах А и out:
равно отношению выходных сопротивлений в узлах А и out:
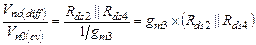 (5.31)
(5.31)
Поскольку же в выходной цепи складываются квадраты шумовых токов и напряжений, то 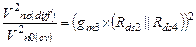 (5.32)
(5.32)
Очевидно, что шумом транзистора М0, как синфазным, с полным правом можно пренебречь.
Итак, будем считать, что квадрат спектральной плотности шумового тока в выходной цепи дифкаскада на рис. 5.6 равен арифметической сумме спектральных плотностей шумовых токов четырех транзисторов (то же самое – и для квадрата полного шумового тока):
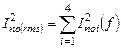 (5.33)
(5.33)
Используем известное соотношение 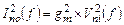 для квадрата спектральной плотности шумового тока
для квадрата спектральной плотности шумового тока 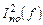 транзистора, где
транзистора, где 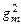 – квадрат крутизны этого транзистора, а
– квадрат крутизны этого транзистора, а 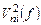 – квадрат спектральной плотности приведенного ко входу шумового напряжения этого транзистора. Последнее является суммой квадратов приведенных ко входу транзистора спектральных плотностей двух шумовых напряжений: во – первых, «белого» (независящая от частоты спектральная плотность) шума резистивного канала
– квадрат спектральной плотности приведенного ко входу шумового напряжения этого транзистора. Последнее является суммой квадратов приведенных ко входу транзистора спектральных плотностей двух шумовых напряжений: во – первых, «белого» (независящая от частоты спектральная плотность) шума резистивного канала 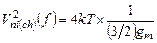 (5.34)
(5.34)
и, во – вторых, 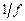 шума
шума 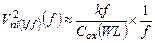 (5.35)
(5.35)
Здесь 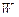 и
и 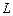 – эффективные ширина и длина канала транзистора;
– эффективные ширина и длина канала транзистора; 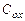 – удельная емкость подзатворного диэлектрика;
– удельная емкость подзатворного диэлектрика; 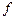 - частота, а
- частота, а 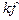 – константа, зависящая от типа транзистора и, особенно, от технологического процесса.
– константа, зависящая от типа транзистора и, особенно, от технологического процесса.
Квадрат напряжения полного шума в диапазоне частот равен интегралу суммы спектральных плотностей (5.33) и (5.34) в этом диапазоне.
Квадрат полной спектральной плотности шумового тока каналов транзисторов равен, ввиду симметричности дифкаскада:
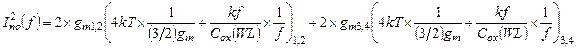
(5.36)
Пусть М1 является входным транзистором дифкаскада. Тогда квадрат спектральной плотности шумового напряжения 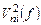 , приведенный к затвору М1 равен
, приведенный к затвору М1 равен
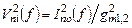 (5.37)
(5.37)
Полная мощность шума на выходе дифкаскада равна интегралу по частоте суммы спектральных плотностей шума от транзисторов M1 – M4:
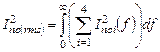 (5.38)
(5.38)
Дата добавления: 2022-02-05; просмотров: 560;











