МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ С НЕСКОЛЬКИМИ ВЫХОДАМИ

При синтезе логических устройств с n входами и m выходами минимизация может проводиться независимо для каждого выхода. Однако, в целом такое устройство может оказаться не минимальным. Дополнительная минимизация может быть проведена путем использования общих элементов, общих минтермов, импликант для формирования различных выходных сигналов. Из этих соображений приведение каждой из выходных функций к минимальной форме не является условием получения минимального в целом устройства. При минимизации устройства в целом некоторые функции и импликанты лучше оставить в неминимальной форме, если они будут общими для нескольких выходов. Если функции имеют общие члены, то можно провести их совместную оптимизацию, выражая одну функцию через другую или вводя промежуточные функции, которые могут быть реализованы один раз и использованы при построении нескольких функций.

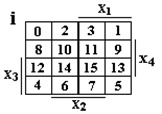
В качестве примера минимизации ЛФ с несколькими функциями рассмотрим синтез преобразователя кода 8421 в код 2421.

Обозначим входные переменные, соответствующие отдельным разрядам кода 8421,- Х4,Х3,Х2,Х1, а выходные переменные кода 2421 - Y4,Y3,Y2,Y1.

Каждый из разрядов кода 2421 Y4, Y3, Y2, Y1 можно рассматривать как функцию от аргумента Х4, Х3, Х2, Х1:

Y4 = f4 ( Х4 , Х3 , Х2 , Х1 ) ; Y3 = f3 ( Х4 , Х3 , Х2 , Х1 ) ;

Y2 = f2 ( Х4 , Х3 , Х2 , Х1 ) ; Y1 = f1 ( Х4 , Х3 , Х2 , Х1 ).

Рис.34. Схема расположения минтермов (указано их десятичное представление для расположения переменных Х4Х3Х2Х1).

Для каждой функции заполняем карту Карно и проводим минимизацию.

__ __

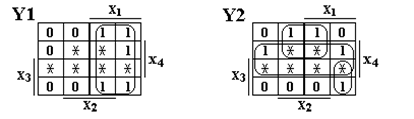Y1 = X1; Y2 = X4 + X2 X3 + X1 X2 X3.

__

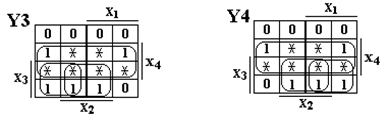
Y3 = X4 + X1 X3 + X2 X3; Y4 = X4 + X1 X3 + X2 X3.

Преобразуем к базису И-НЕ:

Y1 = X1;

;

.

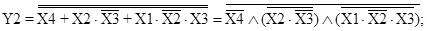
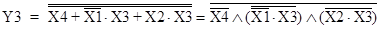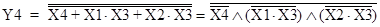Проанализируем выражения и выделим общие слагаемые:

.

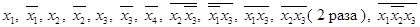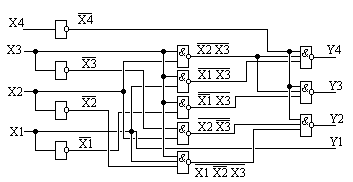
Рис.35. Схема преобразователя кодов в базисе И-НЕ.