Средняя квадратическая ошибка функций
Измеренных величин
В тех случаях, когда используются косвенные методы измерений, ошибка результата зависит как от ошибок измеренных величин, так и от действий (функций), с помощью которых вычислен искомый результат. Поэтому определение ошибок функций измеренных величин mf имеет большое практическое значение. Пусть имеем в общем виде функцию от многих независимых величин:
Z = f(l1, l2, ….ln).
С учетом ошибок измерений величин l можно записать:
Z+ ΔZ= f(l1+Δl1, l2+Δl2,…. ln+Δln).
Поскольку Δl1,Δl2,…Δln, то функцию можно разложить в ряд Тейлора, ограничиваясь членами первого порядка. При разложении в ряд возникают частные производные, поскольку в уравнении имеются несколько переменных аргументов. Не вдаваясь в детализацию вывода, запишем итоговую формулу для определения квадрата средней квадратической ошибки функции нескольких переменных:
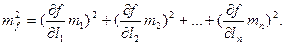
Таким образом, квадрат среднеквадратической ошибки функции общего вида равен сумме квадратов произведений частных производных по каждому аргументу на среднеквадратическую ошибку соответствующего аргумента.
В частности для функции в виде суммы (разности) аргументов вида:
Z = X ± Y ± T ± U ± ... ±V,
будем иметь:
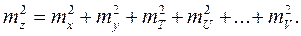
Для функции вида Z = kX, соответственно 

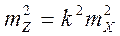
 или
или 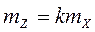 .
.
Дата добавления: 2022-02-05; просмотров: 510;











