Средняя квадратическая ошибка измерений
Для оценки точности измерений, то есть для определения степени близости результата измерения к истинному значению измеряемой величины, чаще всего определяют среднюю квадратическую ошибку. Эта величина определяется по результатам измерений по формуле, предложенной Гауссом:
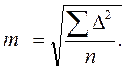
Величина m является также случайной величиной, зависит от числа измерений и сама определяется с ошибкой:
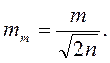
Для определения допустимости полученной ошибки вычисляют предельную ошибку Δпр, больше которой ошибки относятся уже к грубым.
Величину предельной ошибки определяют по формуле:
Δпр =km, где k = 2 (вероятность 0.95) или 3 (вероятность 0.997).
Точность геодезических измерений характеризуется абсолютными и относительными ошибками. Абсолютнымиявляются истинные, средние квадратические и предельные. Относительной ошибкой ε называется отношение соответствующей абсолютной ошибки к истинному значению измеряемой величины. Ее выражают в виде дроби, где в числителе 1.
Если измеренную величину обозначить Хср, то
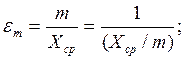
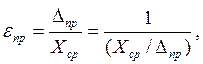
где εm и εпр - соответственно относительная средняя квадратическая и предельная ошибки.
Вычисление среднеквадратической ошибки по формуле Гаусса возможно только тогда, когда известны истинные ошибки измерений, однако в большинстве случаев они не известны. Поэтому на практике задача решается через уклонения результатов измерений от их арифметического среднего v (вероятнейшие ошибки), которые вычисляются по результатам многократных измерений. В этом случае среднеквадратическая ошибка вычисляется по формуле Бесселя:
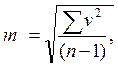
где v - вероятнейшие ошибки: vi = Xi - Xср.
Дата добавления: 2022-02-05; просмотров: 472;











