Основные геодезические задачи

Прямая геодезическая задача заключается в определении плановых координат точки на местности по известным координатам соседней точки, дирекционному углу линии между двумя точками, и длине этой линии (рис. 1.24).

Из рисунка 1.24 видно: X_C = X_B + ΔX_BC; Y_C = Y_B + ΔY_BC, где ΔX_BC и ΔY_BC – приращения координат.

Приращения координат вычисляются по формулам:

ΔX_BC = d_BC cosα_BC, ΔY_BC = d_BC sinα_BC.

Обратная геодезическая задача заключается в определении длины горизонтальной проекции расстояния между точками А и В с известными плановыми координатами, а также дирекционного угла линии АВ.

Из того же рис. 1.24 имеем: ΔX_BC = X_C - X_B, ΔY_BC =Y_C - Y_B,

tgα = ΔY_BC/ ΔX_BC, α_BC =arc tg(ΔY_BC/ ΔX_BC), d_BC = ΔY_BC /sinα_BC =

= ΔX_BC /cosα_BC =( (ΔX_BC)² + (ΔY_BC)²)^0.5.

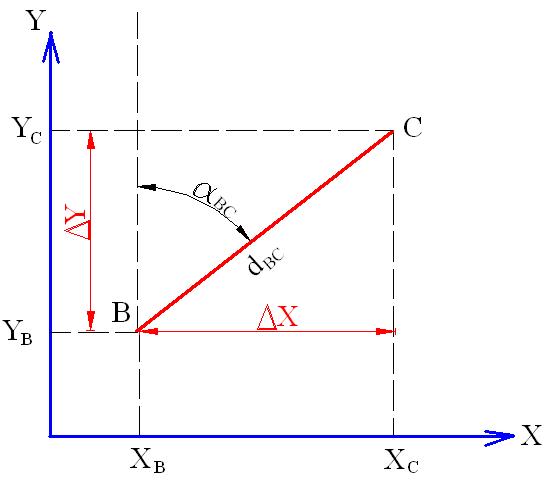
Рис. 1.24. Прямая и обратная геодезические задачи.

Прямая геодезическая засечка заключается в определении координат точки М по известным координатам двух точек А и В и углам засечки ß₁ и ß₂ (рис. 1.25).

Решением обратной геодезической задачи определяют d₁ и дирекционный угол α_AB. Измерив углы ß₁ и ß₂, вычисляют длины сторон S₁ и S₂:

S₁ = d₁ sin(ß₂)/sin(ß₂ + ß₁); S₂ = d₁ sin(ß₁)/sin(ß₂ + ß₁)

и дирекционные углы α_AM = α_AB - ß₁; α_ВM = α_BА + ß₂. Далее, решая прямую геодезическую задачу, определяют координаты точки М.

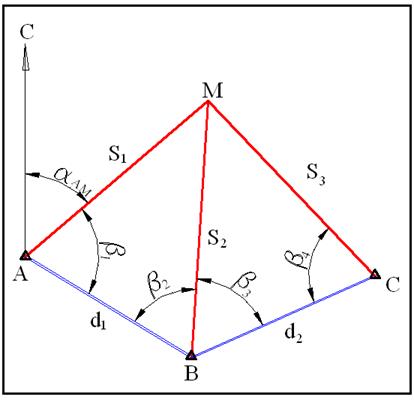
Рис. 1.25. Прямая геодезическая засечка.

Для контроля повторяют измерения со следующей стороны съемочного обоснования ВС. Расхождение в координатах не должно превышать 1/1000 от величины (d₁ + d₂)/2.

Обратная геодезическая засечка состоит в определении координат четвертого пункта (М) по известным координатам трех пунктов А, В, С и двум углам ß₁ и ß₂, измеренным на определяемом пункте М на исходные пункты А, В, С (рис. 1.26).

Обозначим дирекционный угол стороны МА через α₁, тогда дирекционный угол стороны МВ: α₂ = α₁ - ß₁, а для стороны МС имеем: α₃ = α₁ – (ß₁ + ß₂).

Для сторон МА, МВ и МС решаются обратные геодезические задачи:

Y_М - Y_А =( Х_М - Х_А)tg α₁;

Y_М - Y_B =( Х_М - Х_B)tg α₂;

Y_М - Y_C =( Х_М - Х_C)tg α₃.

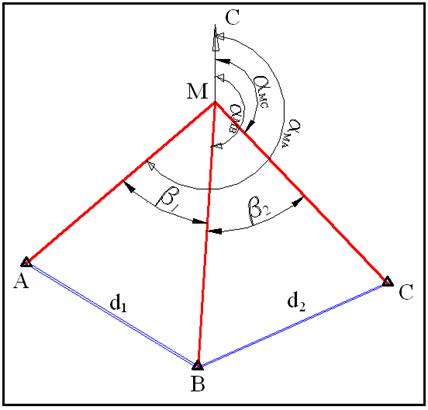
Рис. 1.26. Обратная геодезическая засечка.

Эти три уравнения однозначно определяют три неизвестных величины X_М, Y_M, α₁. Однако в этом случае координаты точки М определяются без контроля. Для контроля необходим 4-й пункт и измеренный для него горизонтальный угол.

Каждый вид засечки имеет достоинства и недостатки. Для обратной засечки требуется производить измерения только с определяемого пункта. При прямой засечке - на трех пунктах, тратя время на переходы и перестановки приборов.

Но наличие 3-х исходных пунктов позволяет выполнить прямую засечку с контролем, а обратную - без контроля.

Поэтому в каждом конкретном случае выбирается наиболее целесообразный способ.