Статистичні критерії перевірки нульової гіпотези

Як з’ясувалося, висунута гіпотеза може бути хибною, тому виникає необхідність її перевірки.

Оскільки перевірка проводиться статистичними методами, то її називають статистичною.

Статистична значимість, або р-рівень значимості – це основний результат перевірки статистичної гіпотези. Інакше кажучи, це ймовірність того, що знайдений зв’язок носить випадковий характер, а не є властивістю сукупності. Саме статистична значимість є кількісною оцінкою надійності зв’язку: чим менша ця ймовірність, тим надійніший зв’язок.

Чим менше значення р-рівня, тим вища статистична значимість результату дослідження, що підтверджує наукову гіпотезу.

При прийнятті рішень за допомогою гіпотез можуть статися помилки двох родів.

Помилка першого роду полягає в тому, що буде відкинута правильна гіпотеза.

Помилка другого роду полягає в тому, що буде прийнята неправильна гіпотеза.

Ймовірність здійснити помилку першого роду позначають через 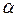, Число 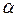задають малим і найчастіше використовують значення 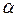, що дорівнюють 0,05, 0,01 і так далі.

Якщо, наприклад, 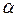= 0,01, то це означає, що в одному випадку із 100 є ризик допустити помилку першого роду.

Для перевірки гіпотез вибирається статистичний критерій, який умовно позначають через К, де К – випадкова величина, закон розподілу якої відомий.

Означення. Статистичним критерієм або статистикою критерію називають випадкову величину K, яка є основою для перевірки нульової гіпотези.

Для різних гіпотез статистичні критерії є різними.

Множину R значень статистичного критерію К можна розбити на дві підмножини, що не перетинаються – і .

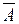Означення. Значення статистичного критерію підмножини , при яких нульова гіпотеза приймається, називається областю прийняття гіпотези, а значення, при яких гіпотеза Н₀ відхиляється критичною областю.

За характером критичні області поділяються на односторонні та двосторонні.

Області А і 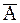(прийняття гіпотез і критичні) між собою розділяються точками, які називаються критичними і позначати k_кр

Означення. Правосторонню критичною областю називається така область, для якої виконується нерівність К> k_кр

Відповідно критична область буде лівосторонньою, якщо виконується нерівність К < k_кр.

Означення. Двохсторонньою називають критичну область, яка задовільняє нерівності К< k_кр1 і К> k_кр2

У більшості випадків для двосторонньої критичної області точки k_кр1 і k_кр2 розташовані симетрично відносно нуля, тобто k_кр1 =-k_{кр 2}.

Перевірка статистичних гіпотез будь-якої природи може бути описана за допомогою такої загальної схеми:

1. Формулюється статистична гіпотеза Н₀.

2. Вибирається статистичний критерій відповідно до сформульованої гіпотези Н₀.

3. Залежно від нульової гіпотези Н₀ і альтернативної Н₁ вибирається одностороння або двостороння критична область.

Для побудови критичних областей, необхідно знайти значення критичних точок.

В основі побудови критичної області лежить принцип практичної неможливості здійснення малоймовірної випадкової події при одній спробі, тому задається мала величина ймовірності 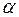( 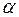=0,01; 0,05) – рівень значущості критерію перевірки правильності гіпотези Н₀: на основі відомого розподілу ймовірності критерію К визначається за допомогою спеціальних таблиць критична точка k_кр. По знайденому значенню k_кр.. відповідно будується лівостороння, правостороння або двостороння критична область.

4. За результатами вибірки обчислюється спостережуване (емпіричне) значення критерію К^* (К_спост.)

5. Виходячи з вимоги, що при правильності гіпотези Н₀ ймовірність того, що К^* потрапить у критичну область має дорівнювати прийнятому рівню значимості a, перевіряється статистична гіпотеза.

Для визначення критичної області критичні точки шукають із таких співвідношень:

а) для правосторонньої критичної області: Р{К > k_кр }=a, (k_кр>0);

б) для лівосторонньої критичної області: Р{К < k_кр }=a, (k_кр<0);

в) для двосторонньої симетричної критичної області:

Р{К > k_кр }= , (k_кр >0);

Якщо К^* потрапляє у критичну область, а це подія малоймовірна і вона все таки здійснилася, то нульова гіпотеза Н₀ відхиляється. У протилежному випадку – приймається.

Зрозуміло, що для певної гіпотези можна побудувати багато різних критеріїв її перевірки, і за кожним критерієм можемо отримати різні результати щодо прийняття нульової гіпотези на основі тієї самої вибірки, тому для визначення кращого критерію вводиться характеристика, яка називається потужністю критерію.

Означення. Потужністю критерію називають ймовірність потрапляння критерію у критичну область за умови, що конкуруюча гіпотеза є істинною.

Тобто потужність критерію визначається як ймовірність не допустити помилку другого роду при вибраному критерію.

За своїм змістом статистичні гіпотези можна поділити на декілька основних видів:

- про рівність числових характеристик генеральних сукупностей;

- про числові значення параметрів;

- про закон розподілу;

- про однорідність вибірок (тобто належність їх одній і тій генеральній сукупності);

- про стохастичну незалежність елементів вибірки.

Розглянемо перевірку декількох з основних гіпотез та умови їх прийняття.