Практичне заняття №14

Тема: Точкові та інтервальні оцінки

Мета: сформувати у студентів уявлення про точкові та інтервальні оцінки, навчити знаходити довірчі інтервали для математичного сподівання, дисперсії та середнього квадратичного відхилення.

План заняття

1. Точкові оцінки. Інтервальні оцінки.

2. Довірчі інтервали для математичного сподівання.

3. Довірчі інтервали для дисперсії.

рекомендована Література

1. Теорія ймовірностей та математична статистика: Навч. посібник для студентів вузів/ В.В. Барковський, Н.В. Барковська Н.В., О.К. Лопатін. 3-є вид. перероб. і доп.– К.: Центр навчальної літератури, 2002. С. 219-248.

2. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ Н.Ш. Кремер. -3-е изд., перераб. и доп.- М.: Юнити, 2007. – С. 308-318.

3. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев. –М.: Даликов и К, 2008. –С.245-267.

4. Теория вероятностей и математическая статистика: Учебное пособие для студентов вузов/ Ред. В.И. Єрмаков. –М.: Инфра-М, 2008. –С.-79-97.

5. Теория вероятностей и математическая статистика: примеры и задачи: Учебное пособие для студентов вузов/ И.В. Белько, Г.П. Свирид. -3-е изд., стереотип.–М.: Новое знание,2007. С.121-143.

6. Посібник з теорії ймовірності та математичної статистики: Навч. посібник для вузів/ М.К. Бугір. – Тернопіль: Підручники і посібники, 1998. –С. 110-113.

7. Прикладные задачи теории вероятности/ Е.С. Вентцель, Л.А. Овчаров. –М.: Радио и связь, 1983. –С.458-462.

8. Статистика (з програмованою формою контролю знань): математична статистика. Загальна теорія статистики: Навчальний посібник для студентів вузів/ А.Т. Опря. -К.: Центр навчальної літератури, 2005. –С. 74-101.

9. Практикум з математичної статистики: Навчальний посібник для студентів вузів/ А.Т. Мармоза. –К.: Кондор, 2004. –С.65-100.

Методичні рекомендації

При підготовці даної теми з’ясувати сутність таких понять як точкова оцінка, інтервальна оцінка, надійність надійний (довірчий) інтервал, рівень значущості. Знати загальний вигляд довірчих інтервалів для математичного сподівання при відомому та невідомому середньому квадратичному відхиленні, для дисперсії. Вміти дати пояснення всіх позначень з формул, а також правила знаходження критичних точок за відповідними таблицями.

Задачі для самоконтролю

Задача 1. Випадкова величина Х має нормальний закон розподілу з відомим середнім квадратичним відхиленням 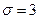і середнім квадратичним відхиленням 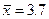. Знайти надійний інтервал для оцінки невідомого математичного сподівання, якщо 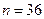, а .

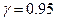Відповідь: 2,72< a <3,68.

Задача 2. Кількісна ознака Х генеральної сукупності розподілена нормально. По вибірці обсягу n=16 знайдені вибіркова середня 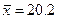і виправлене середнє квадратичне відхилення 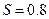. Оцінити невідоме математичне сподівання за допомогою інтервалу довір’я з надійністю 0,95.

Відповідь: 19,74< a <20,63.

Задача 3. Кількісна ознака Х генеральної сукупності розподілена нормально. По вибірці обсягу n=16 знайдене виправлене середнє квадратичне відхилення 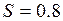. Знайти надійні інтервали для дисперсії при надійності .

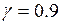Відповідь: .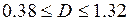

Самостійна робота

Самостійна робота модуля передбачає:

I. Вивчення теми, що винесена на самостійне опрацювання;

II. Модульний тестовий контроль;

ІІІ. Модульна контрольна робота.

І. На самостійне опрацювання винесена тема модуля: Довірчий інтервал для оцінки дисперсії нормально розподіленої випадкової величини.

Зміст теми студентами конспектується в зошиті для практичних занять та входить в модульний тестовий контроль та модульну контрольну роботу. Максимальна кількість балів – 3б.

Методичні рекомендації

При підготовці даної теми повторити властивості нормально розподіленої величини, врахувати те, що точковою оцінкою для параметра σ є виправлене середнє квадратичне відхилення s, а це означає, що для знаходження меж інтервалу потрібно розв’язати рівняння: P{|σ −s|<δ}=γ Û P{s−δ <σ <s+δ}=γ.

Шуканий інтервал буде дорівнювати 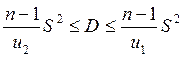, де , .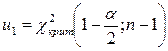

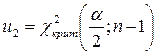Приклад. Кількісна ознака Х генеральної сукупності розподілена нормально. По вибірці обсягу n=16 знайдене виправлене середнє квадратичне відхилення 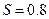. Знайти довірчий інтервал для дисперсії при надійності .

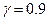Розв’язання. Довірчий інтервал для дисперсії має вигляд: 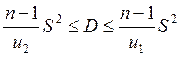, де , .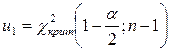

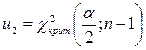Знаходимо значення 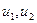(додаток 4). Маємо

.

.

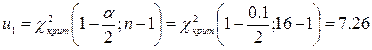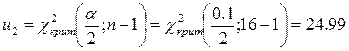Тоді довірчий інтервал матиме вигляд: .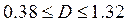

ІІ. Модульний тестовий контроль передбачає тест, що складається з 11 тверджень. Підтвердження студентом істинності чи хибності кожного з тверджень приносить йому 1бал. Отже, максимальна кількість балів – 11.

Орієнтовні варіанти тверджень

1. Випадковий відбір здійснюється жеребкуванням.

2. В інтервальному варіаційному ряді не може бути менше 8 інтервалів.

3. Розмах вибірки – це різниця між найбільшою та найменшою варіантами.

4. Емпірична функція розподілу, побудована за інтервальним варіаційним рядом, є неперервною.

5. Для обчислення числових характеристик за дискретним варіаційним рядом з рівновіддаленими варіантами зручно користуватися методом умовних варіант.

6. Вибіркове середнє обчислюють за формулою: .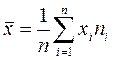

7. 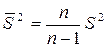- виправлена дисперсія.

8. Нехай дано вибірку 1, 2, 2, 3, 4, 5, 6. Тоді х_в=3,29

9. У модального інтервалу найбільша накопичена частота.

10. Мода та медіана, знайдені за інтервальним варіаційним рядом, збігаються.

11. Інтервальна оцінка невідомого параметра визначається декількома числами.

ІІІ. Модульна контрольна робота передбачає п’ять завдань, правильний результат якого оцінюється в 1 бал. Отже, максимальна кількість балів за модульну контрольну роботу – 5.

1. За вибіркою А побудувати дискретний варіаційний ряд, а за вибіркою В – інтервальний варіаційний ряд.

2. За вибіркою В побудувати емпіричну функцію розподілу, її графік, гістограму відносних частот.

3. За вибіркою А (дискретний ряд) обчислити числові характеристики.

4. За вибіркою В (інтервальний ряд) обчислити числові характеристики.

5. За вибіркою А знайти надійні інтервали для математичного сподівання та дисперсії при рівні значущості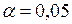

Орієнтовний варіант завдання

Вибірка А: 1,5,4,6,8,4,5,1,1,2,3,4,5,7,7,8,8,1,4,14

Вибірка В (кількість інтервалів 6):

10,11,25,23,15,15,14,17,15,33,37,36,25,14,10,11,15,12,13,32,31,30,30,24,35,35,26,28,21,26.

Індивідуальні варіанти завдань для кожного студента знаходяться в додатку 8. Порядковий номер прізвища студента в списку групи визначає номер варіанта індивідуального завдання.