Елементи теорії напруженого стану та гіпотези міцності

Розрахунки на міцність стержнів при складному деформуванні

У практиці реальних розрахунків на міцність та жорсткість елементів машинобудівних конструкцій дуже рідко можна зустріти випадки простих видів деформування. Більш поширені випадки сумісної дії крутних та згинальних моментів, наприклад, у валах редукторів. При наявності косозубих коліс додатково діють поздовжні сили. У перерізах просторових рам діє більшість з можливих внутрішніх силових факторів, а у точках перерізів − складний напружений стан. Тому вкрай необхідно розглянути особливості розрахунків напружено-деформованого стану стержньових елементів при довільному навантаженні та надати рекомендації при рішенні задач міцності та жорсткості для деяких характерних випадків складного навантаження.

Елементи теорії напруженого стану та гіпотези міцності

Як відомо, мірою інтенсивності внутрішніх зусиль, що діють у довільному перерізі стержня, є так звані напруження. Отже, напруженням називається внутрішня сила, віднесена до одиниці площі в даній точці перерізу. В залежності від розташування напруження відносно площини відокремлюють нормальні − σ та дотичні − τ напруження. Їх вимірюють у паскалях (Па), або кратних йому одиницях (МПа).

При дослідженні напруженого стану тіла в окремій точці В (рис. 1.1 а) поблизу неї завдяки гіпотезі про суцільність матеріалу можливо виділити нескінченно малий об’єм у вигляді паралелепіпеда, грані якого паралельні координатним площинам декартової системи координат. На цих гранях діють внутрішні зусилля, які замінюють дію відкинутої частини тіла. Отже, можна вважати, що на гранях цього паралелепіпеда діють нормальні і дотичні напруження (рис. 1.1 б), що внаслідок його малості рівномірно розподілені по площинам.

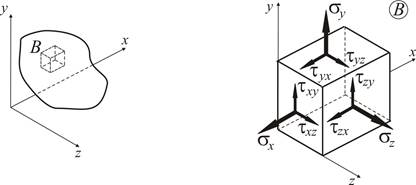
а б

Рисунок 1.1

На рис. 1.1. б зображені додатні значення нормальних і дотичних напружень з урахуванням правила індексів: нормальні напруження позначають літерою σ з індексом, що відповідає осі системи координат, що є перпендикулярною до відповідної грані паралелепіпеда; дотичне напруження позначається літерою τ з двома індексами − перший відповідає напряму осі, що є перпендикулярною до відповідної площини, а другий − напряму осі, паралельно якої розташований вектор дотичного напруження. Вибір орієнтації декартових осей є довільним. Таким чином, на шести гранях нескінченно малого паралелепіпеда діють дев’ять компонент напружень. Але не всі вони є незалежними. Враховуючи закон парності дотичних напружень ( 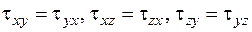) [1], кількість незалежних компонент напружень у кожній точці тіла зменшуємо до шести: трьох нормальних та трьох дотичних ( ).

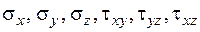Шість компонент напружень повністю визначають напружений стан у довільній точці тіла. При іншому виборі системи координат змінюється розташування граней паралелепіпеда, тому зміняться і значення координатних напружень у точці, але напружений стан залишиться тим самим. При цьому, через точку завжди можна провести такі площадки, на яких дотичні напруження дорівнюватимуть нулю [2]. Площадки, на яких дотичних напружень немає, називають головними площадками, а нормальні напруження, що діють на цих площадках, − головними напруженнями. Зауважимо, що деякі значення цих головних напружень у точці можуть дорівнювати нулю. Напрями, що паралельні головним напруженням, називають головними осями в даній точці. Можна показати [2], що у кожній точці завжди є три взаємно перпендикулярні головні площадки і головні осі.

Головні напруження позначаються 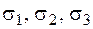у порядку зменшення значень з урахуванням знака напруження ( 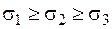). Отже, напружений стан у точці можна зобразити у вигляді елементарних паралелепіпедів, на гранях яких діють тільки нормальні (головні) напруження (рис. 1.2).

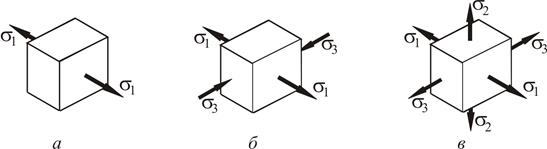
Рисунок 1.2

По вигляду напруженого стану у головних напруженнях можна класифікувати види напруженого стану у точці:

− якщо тільки одне головне напруження не є нульовим (рис. 1.2 а), напружений стан називається одновісним або лінійним;

− якщо два головних напруження не є нульовими, то такий напружений стан називається двовісним або плоским (рис. 1.2 б, );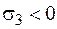

− напружений стан, у якому всі три головні напруження не дорівнюють нулю, називається тривісним або об’ємним (рис. 1.2 в).

Зауважимо, що в задачах опору матеріалів зустрічаються види напружених станів тільки першого та другого типів. Так, при розтяганні стержнів та при чистому згині балок маємо одновісний напружений стан, а у задачах згинання з крученням, та при дії довільної системи сил на брус, що розглядаються у цьому посібнику, у деяких точках має місце плоский напружений стан.

На рис. 1.3 зображено плоский напружений стан у довільній точці В, як у головних площадках (а), так і в системі координат, що зв’язана з осями стержня (б).

Найбільш важливим завданням інженерних розрахунків після визначення напруженого стану в найнебезпечних точках конструкції є оцінка її міцності. При простих видах деформування та при одновісних напружених станах ця задача розв’язується при використанні умов міцності, в які входять експериментально визначені граничні напруження, що відповідають простим видам деформування, що розглядаються (розтягання, кручення).

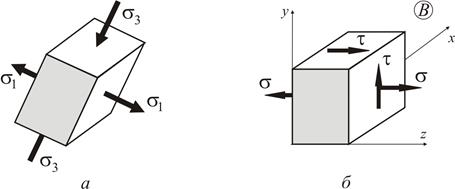
Рисунок 1.3

Небезпечним вважають відповідне напруження, при якому в залежності від стану матеріалу (крихкий чи пластичний) починається руйнування або виникають залишкові деформації. Щоб унеможливити виникнення небезпечного стану визначаються допустимі напруження, що є меншими ніж небезпечні, тим самим забезпечуючи міцність конструкції з деяким коефіцієнтом запасу. Так, випробування зразків пластичного матеріалу на одновісне розтягання, дає можливість визначити границю текучості 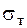та допустиме напруження 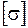. А умова міцності для одновісного напруженого стану набуває вигляду:

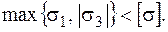
При двовісних, чи тривісних напружених станах, як показують експериментальні дослідження, небезпечний стан може наступити при різних співвідношеннях головних напружень і різному їх граничному значенні. А оскільки провести експериментальні дослідження по виявленню небезпечного напруженого стану для всіх матеріалів при різних можливих співвідношеннях головних напружень практично неможливо, то цю проблему розв’язують за допомогою різних теорій міцності, що мають в основі гіпотези про переважний вплив на міцність матеріалу деякого фактора, наприклад, найбільшого дотичного напруження, чи питомої потенційної енергії формозміни. Ці фактори при небезпечному напруженому стані набувають критичних значень, що можуть бути визначеними з простих випробувань.

Теорії міцності дають можливість замість реального складного напруженого стану розглядати рівнонебезпечний одновісний напружений стан. Це досягається введенням поняття еквівалентного напруження одновісного розтягання 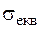та коефіцієнту запасу n , під яким розуміють число, що показує, в скільки разів потрібно одночасно збільшити всі компоненти даного складного напруженого стану, щоб він став граничним. Це означає, що у стільки же разів треба збільшити і еквівалентне напруження одновісного розтягання для досягнення небезпечного стану. Тоді

.

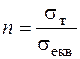Нараду з багатьма сучасними, дослідники нараховують п’ять класичних теорій міцності, що пронумеровані у хронологічному порядку. Але для розрахунків на міцність у машинобудуванні найбільш поширені дві з них: III (третя) та IV (четверта), які застосовуються для пластичних матеріалів.

Третя теорія міцності, чи критерій найбільшого дотичного напруження, полягає у припущенні, що небезпечний напружений стан виникає тоді, коли найбільше дотичне напруження 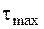досягає небезпечного значення. А оскільки 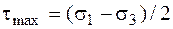для даного складного напруженого стану і 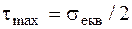для рівнонебезпечного одновісного еквівалентного напруженого стану [2], то умова міцності набуває вигляд

,

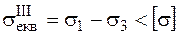де «ІІІ» означає «третя теорія міцності».

Для застосування у практичних розрахунках на міцність стержнів при згині з крученням, де здебільшого має місце плоский напружений стан, більш прийнятна інша форма математичного запису цієї теорії через напруження у поперечному перерізі стержня:

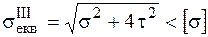. (1.1.1)

Четверта теорія міцності, або критерій питомої потенційної енергії деформації формозміни, приймає як критичний параметр вказану питому енергію, яка може бути підрахована через компоненти даного складного напруженого стану [2]. Наведемо умову міцності за цією теорією для плоского напруженого стану в точці для стержнів:

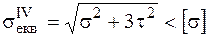. (1.1.2)