Дискретні випадкові величини
З кожною випадковою величиною пов’язана деяка множина чисел – значень, які вона може приймати. В результаті проведення випробування ці значення мають різні ймовірності їх появи. Для повної характеристики випадкової величини потрібно вказати не лише усі її можливі значення, але й закон, за яким знаходиться ймовірність кожного значення pk=p(X=xk)=f(X) або P(X). Правило, що встановлює зв’язок між можливими значеннями та їх ймовірностями, називають законом розподілу випадкової величини. У випадку ДВВ функціональну залежність можна задавати таблично, аналітично або графічно.
Означення. Законом розподілу дискретної випадкової величини називається співвідношення, що встановлює зв’язок між можливими її значеннями та відповідними їх ймовірностями.
Нехай ДВВ Х приймає одне з п різних значень х1, х2, х3, ..., хn. При цьому кожне з цих значень величина Х приймає з визначеною ймовірністю – відповідно р1, р2, р3, ..., рn. Якщо ці дані помістити в таблицю, то така таблиця називається таблицею розподілу ДВВ Х або рядом розподілу ДВВ Х, й говорять, що величину подано таблично.
| Х | х1 | х2 | х3 | х | ... | хп |
| р | р1 | р2 | р3 | р4 | ... | рп |
Оскільки випадкова величина Х неодмінно прийме якесь значення, то 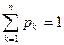 .
.
За рядом розподілу можна побудувати функцію розподілу (ймовірності) дискретної випадкової величини Х
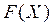 =
= 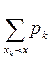 ,
,
де підсумовування проводиться за всіма k, для яких хк < х.
Графік функції розподілу дискретної випадкової величини має ступінчастий вигляд. Переконаємося у цьому на прикладі.
Задача 1. В партії з шести деталей чотири стандартні. Навмання вибрані три деталі. Знайти:
а) ряд розподілу дискретної випадкової величини Х – число стандартних деталей серед відібраних;
б) функцію розподілу дискретної випадкової величини Х.
Розв’язання
а) Випадкова величина Х може приймати такі значення: х1=1, х2=2, х3=3. Знайдемо ймовірності цих значень
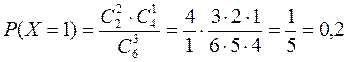 ;
;
 ;
;
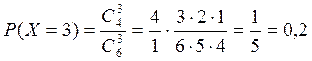 .
.
Отже, маємо ряд розподілу дискретної випадкової величини Х:
| х | |||
| р | 0,2 | 0,6 | 0,2 |
Перевірка: 0,2+0,6+0,2=1.
б) побудуємо функцію розподілу дискретної випадкової величини Х та її графік:
якщо х <1, то 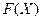 =0;
=0;
якщо 1≤ х<2, то 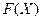 =0,2;
=0,2;
якщо 2≤ х<3, то 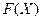 =0,2+0,6=0,8;
=0,2+0,6=0,8;
якщо х≥3, то 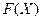 =0,2+0,6+0,2=1.
=0,2+0,6+0,2=1.
Отже,

Будуємо графік

Дата добавления: 2022-02-05; просмотров: 484;











