Основні закони розподілу неперервних величин
Основні закони розподілу неперервних величин розрізняють за виглядом їх диференціальних функцій розподілу, тобто щільності ймовірностей 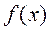 .
.
1. Рівномірний розподіл
Величина Х розподілена рівномірно на проміжку (а;b), якщо усі її можливі значення належать цьому проміжку, а щільність її ймовірностей у цьому проміжку постійна, тобто
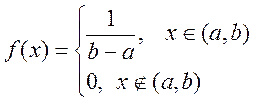 .
.
Якщо Х розподілена рівномірно на проміжку (а;b), то ймовірність належності Х будь-якому інтервалу (х1;х2) 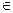 (а;b) пропорційна довжині цього інтервалу:
(а;b) пропорційна довжині цього інтервалу:
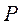 (х1<Х<х2)=
(х1<Х<х2)= 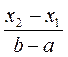 ,
, 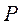 (a<Х<b)=1.
(a<Х<b)=1.
Цьому закону розподілу підлягають похибки округлення різноманітних розрахунків.
Графік щільності рівномірного розподілу має вигляд рис. 5.

2. Показниковий розподіл
Випадкову величину Х називають розподілену за показниковим законом розподілу, якщо щільність її ймовірностей має вигляд
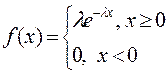 , де
, де 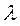 >0.
>0.
Показниковому розподілу задовольняють: час телефонної розмови, час безвідмовної роботи годинника.
Графік щільності показникового розподілу має вигляд рис. 6.

3. Нормальний розподіл
Випадкову величину Х називають розподіленою нормально, якщо щільність її ймовірностей має вигляд
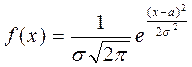 , де а і
, де а і 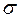 – параметри розподілу.
– параметри розподілу.
Графік щільності нормального розподілу називають кривою Гауса і зображають рис. 7.

1) точки 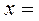
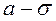 та
та 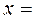
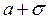 – точки перегину.
– точки перегину.
2) max 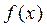 в точці
в точці 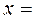
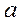 ,
, 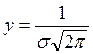 .
.
Для неперервних випадкових величин також можна розглядати числові характеристики. Вони обчислюються за допомогою щільності розподілу.
Дата добавления: 2022-02-05; просмотров: 418;











