Числові характеристики ДВВ

<19 20 212223 24 25 >

Випадкова величина повністю визначається своїм законом розподілу. Але в деяких випадках корисно знати допоміжні числові характеристики розподілу, крім того, інколи ці характеристики є важливішими за сам розподіл випадкової величини.

Математичне сподівання

Нехай маємо ДВВ Х та її таблицю розподілу

Х	х₁	х₂	х₃	х	...	х_п
р	р₁	р₂	р₃	р₄	...	р_п

Означення. Математичним сподіваннямдискретної випадкової величини Х називається сума добутків всіх можливих значень випадкової величини та відповідних їх ймовірностей

М(Х)= 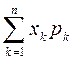(12)

Математичне сподівання називають центром розсіювання випадкової величини і середнім арифметичним спостережуваних значень випадкової величини.

Задача 2. Азартна гра. Кидають два гральні кубики. Якщо сума очок більша 10, то гравець виграє 10 копійок, інакше програє 1 копійку. Чи є сенс йому грати в цю гру 12000000 партій?

Розв’язання. W=36, тому із 36 можливих результатів випробування лише 3 сприятливих для гравця. А закон розподілу матиме вигляд

х		-1
р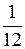

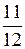
М(Х)= .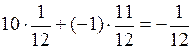

Отже, програючи в середньому 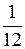копійки за партію, за 12 000000 партій гравець програє 1 000 000 копійок, або 10 000 грн.

Властивості математичного сподівання:

1. Математичне сподівання сталої величини є сама ця стала: М(С)=С;

2. Сталий множник можна виносити за знак математичного сподівання: М(СХ)=СМ(Х);

3. Математичне сподівання суми двох випадкових величин дорівнює сумі їх математичних сподівань: М(Х+У)=М(Х)+М(У);

4. Математичне сподівання добутку двох незалежних випадкових величин дорівнює добутку їх математичних сподівань: М(Х·У)=М(Х) М(У);

Дисперсія та середнє квадратичне відхилення

Математичне сподівання дає відповідь на питання: „Яке значення випадкова величина приймає всередньому?”

Неважко показати, що випадкові величини з рівними математичними сподіваннями можуть суттєво відрізнятися по ступені близькості до нього.

Розглянемо випадкові величини Х та У

Х У

р 0,5 0,5 р 0,5 0,5

Очевидно М(Х)=М(У)=50. Але якщо для випадкової величини Х відхилення від значення 50 незначне, то для випадкової величини У воно суттєве.

Якщо вибір між величинами Х та У – це вибір між двома альтернативними рішеннями, то Х – це більш стабільний передбачуваний результат, а У – це ризик.

Показником такої „непередбачуваності” є ще одна числова характеристика, що називається дисперсією і позначається D(X).

Якщо від випадкової величини відняти її математичне сподівання, то отримаємо нову випадкову величину Х-М(Х). Квадрат останньої також є випадковою величиною (Х-М(Х))², математичне сподівання якої і є дисперсія випадкової величини Х.

Означення. Дисперсією дискретної випадкової називається математичне сподівання квадрата різниці випадкової величини і її математичного сподівання

D(X)=M(X-M(X))² (13)

Дисперсію зручно обчислювати за формулою:

D(X)=M(X²)-(M(X))² (14)

Ця формула випливає безпосередньо з означення після застосування властивостей математичного сподівання.

Обчислимо тепер дисперсії випадкових величин Х та У

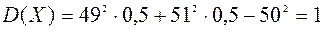
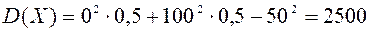
Зауваження: математичне сподівання може бути будь-яким числом, а дисперсія завжди додатне число.

Властивості дисперсії

1. D(C)=0, C – стала величина;

2. D(CX)=C²D(X), тобто сталий множник можна винести за знак дисперсії, піднісши його до квадрату;

3. Дисперсія суми незалежних випадкових величин дорівнює сумі їх дисперсій D(X+Y)=D(X)+D(Y)

Наслідок: D(X-Y)=D(X)+D(Y).

Випадкові величини, що моделюють будь-які об’єкти реального світу, зазвичай мають розмірність (штуки, кілограми, метри і т.п.) При цьому математичне сподівання має туж розмірність, що й сама величина. А розмірність дисперсії дорівнює квадрату розмірності випадкової величини. Для того, щоб уникнути цього вводиться поняття середньоквадратичного відхилення.

Означення. Корінь квадратний з дисперсії називається середнім квадратичним відхиленням випадкової величини і обчислюється за формулою:

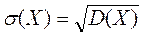(15)

Дисперсія і середнє квадратичне відхилення є мірою розсіяння значень випадкової величини навколо її математичного сподівання.

Задача 3. Дано ряд розподілу дискретної випадкової величини

х

р 0,4 0,5 0,1

Знайти дисперсію та середнє квадратичне відхилення.

Розв’язання. Знайдено математичне сподівання за формулою (12): М(Х)=1·0,4+2·0,5+3·0,1=1,7.

Для знаходження математичного сподівання від квадрата можливих значень, потрібно всі можливі значення випадкової величини піднести до квадрата

Х²

р 0,4 0,5 0,1

М(Х²)= 1·0,4+4·0,5+9·0,1=3,3.

За формулою (14) знаходимо дисперсію D(X)= M(X²)-(M(X))²=3,3-(1,7)²=0,41.

Тоді середнє квадратичне відхилення знаходиться за формулою (15) і дорівнює .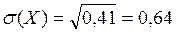

Відповідь: 0,41; 0,64.

<19 20 212223 24 25 >

Дата добавления: 2022-02-05; просмотров: 290;