Практичне заняття №5

Тема: Схема Бернуллі. Граничні теореми.

Мета: сформувати знання граничних теорем та умови їх застосування в схемі Бернуллі, навчити використовувати теореми в різних практичних задачах.

Основні знання, якими повинні оволодіти студенти під час вивчення теми: знати схему Бернуллі, володіти поняттям найімовірнішого числа, знати формулу Бернуллі, знати умови при яких потрібно застосовувати граничні теореми (формулу Пуассона, локальну та інтегральну теореми Муавра-Лапласа).

Основні вміння, якими повинні оволодіти студенти під час вивчення теми: вміти правильно визначати умови за яких застосовуються різні граничні теореми та розв’язувати практичні задачі, визначати найімовірніше число успіхів.

План заняття

1. Схема повторних незалеж­них випробувань. Схема Бернуллі.

2. Формула Пуассона.

3. Властивості локальної та інтегральної функцій Лапласа.

4. Локальна теорема Муавра-Лапласа.

5. Інтегральна теорема Муавра-Лапласа.

рекомендована Література

1. Теорія ймовірностей та математична статистика: Навч. посібник для студентів вузів/ В.В. Барковський, Н.В. Барковська Н.В., О.К. Лопатін. 3-є вид. перероб. і доп.– К.: Центр навчальної літератури, 2002. С. 69-92.

2. Математика для психологов: Учебник /А.Н. Киричевец, Е.В. Шикин, А.Г. Дьячков / Под ред. А.Н. Киричевца. – М.:Флинта: Московский психолого-социальный институт, 2003. С. 237-239.

3. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ Н.Ш. Кремер. -3-е изд., перераб. и доп.- М.: Юнити, 2007. – С. 68-87.

4. Теорія ймовірностей...від найпростішого: Навчальний посібник для студентів вузів/ О. Д. Валь, К.С. Королюк, С.В. Мельничук. –Чернівці: Книги-ХХІ, 2004.-С. 49-65.

5. Основи теорії ймовірностей: курс лекцій: Навч. посібник/ В.М. Рабик. – Львів: Магнолія плюс, 2004. С. 30-38.

6. Курс теории вероятностей: Учебник для студентов вузов/ В.П. Чистяков. – 7-е изд., испр. и доп. –М: Дрофа, 2007.- С. 49-70.

7. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев. –М.: Даликов и К, 2008. - С.39-40.

8. Теория вероятностей и математическая статистика: Учебное пособие для студентов вузов/ Ред. В.И. Єрмаков. –М.: Инфра-М, 2008. –С.22-24.

9. Теория вероятностей и математическая статистика: примеры и задачи: Учебное пособие для студентов вузов/ И.В. Белько, Г.П. Свирид. -3-е изд., стереотип. –М.: Новое знание, 2007. С. 28-39.

10. Посібник з теорії ймовірності та математичної статистики: Навч. посібник для вузів/ М. К. Бугір. – Тернопіль: Підручники і посібники, 1998. –С. 33-39.

11. Основи теорії ймовірностей та математичної статистики: Навчальний посібник для студентів/ В.П. Бабак, А.Я. Білецький, О.П. Приставка, П.О. Приставка.-К.: КВІЦ.,2003. –С.36-44.

12. Математична статистика та задачі оптимізації в алгоритмах і програмах: Навчальний посібник для студентів вузів/ Ю.А.Толбатов. –К.: Вища школа, 1994. –С.20-29.

13. Елементи теорії ймовірностей/ В.М. Резанко. Навч. Посібник 3-тє вид., перероб. і доп. – К.: 2006.-С. 41-49.

Методичні вказівки

1. Опрацювати рекомендовану літературу.

2. Повторити поняття функції з курсу алгебри, а також поняття парності та непарності функції.

3. Вивчити формулу Бернуллі. Звернути увагу на умови при яких формулу Бернуллі застосовувати неможна. Знати формулу для визначення найімовірнішого числа успіхів. Вивчити формулу Пуассона. Вміти сформулювати та записати локальну і інтегральну теореми Муавра-Лапласа, перерахувати умови їх застосування. Звернути увагу на властивості локальної та інтегральної функцій Лапласа та їхні графіки. Ознайомитися з таблицями значень цих функцій.

задачі для самоконтролю

Задача 1.Монету кинуто 6 разів. Знайти ймовірність того що герб випаде 4 рази.

Відповідь: .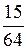

Задача 2. Середній брак при виробництві продукції становить 0,1%. Перевіряється партія з 1000 деталей. Яка ймовірність того, що бракованих буде від 2 до 4 деталей?

Відповідь: .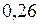

Задача 3. При виробництві деякої продукції ймовірність виготовлення 1-го сорту приймається рівною 0,64. Визначити ймовірність того, що із 100 навмання взятих виробів 70 будуть першого сорту.

Відповідь: .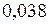

Задача 4. Ймовірність виходу з ладу одного приладу дорівнює 0,1. Визначити ймовірність того, що за час Т зі 100 приладів вийде з ладу від 6 до 18 приладів.

Відповідь: .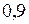

Задача 5. Ймовірність появи події в кожному з 100 незалежних випробувань рівна 0,8. Знайти ймовірність того, що подія з’явиться не менше 75 разів.

Відповідь: .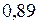

Самостійна робота

Самостійна робота модуля передбачає виконання таких видів робіт:

I. Вивчення тем, що винесені на самостійне опрацювання.

II. Модульний тестовий контроль.

III. Модульна контрольна робота.

IV. Написання реферату.

І. На самостійне опрацювання винесені такі теми модуля:Послідовність випробувань з різними ймовірностями.Проста течія подій.

Методичні рекомендації

При вивченні теми: Послідовність випробувань з різними ймовірностями слід розглянути випадок коли у п незалежних випробуваннях ймовірності появи події А різні, тоді ймовірність появи події А k разів у п випробувань не обчислюється за формулою Бернуллі, а використовується твірна функція

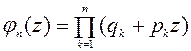
Доведено, що шукана ймовірність 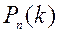дорівнює коефіцієнту, що стоїть при .

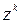При опрацюванні теми: Проста течія подій потрібно знати, що простою течією подій називають послідовність таких подій, які з’являються у випадкові моменти часу. З’ясувати, яка течія подій називається пуассонівською та що таке інтенсивність течії. Особливу увагу слід звернути на математичну модель простої течії подій: якщо течія подій пуассонівська, то ймовірність появи події А k разів за час t можна знайти за формулою 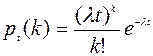, де l – інтенсивність течії.

Наприклад, середня кількість замовлень, що поступають до фотодруку кожну годину, дорівнює 3. Потрібно знайти ймовірність того, що за дві години буде 5 замовлень. Маємо просту течію подій з інтенсивністю l=3.

Підставивши вихідні дані у формулу 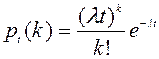отримаємо: .

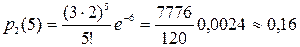ІІ. Модульний тестовий контроль передбачає перевірку теоретичних знань студентів: основних понять, формул, формулювання теорем, правил та умов їх застосування при розв’язуванні практичних занять. Тест є комплексом завдань трьох рівнів: А – низький – 2 бали (0,2 б. за кожну правильну відповідь), Б – достатній – 5 балів (0,5 б. за кожну правильну відповідь), В – високий – 4 бали (1 б. за кожну правильну відповідь), всього 11 балів.

Орієнтовні запитання тесту

Рівень А

1. Сукупність усіх елементарних подій випробування називається:

1) добутком елементарних подій;

2) простором елементарних подій;

3) сумою елементарних подій.

2. Будь-яка підмножина А простору елементарних подій називається:

1) достовірною подією;

2) випадковою подією;

3) неможливою подією.

3. Оберіть правильне твердження:

1) ймовірність достовірної події дорівнює нулю;

2) ймовірність неможливої події дорівнює одинці;

3) ймовірність випадкової події є додатне число, що лежить у межах від нуля до одиниці.

4. Сукупності, складені з будь-яких елементів, які відрізняються одна від одної або елементами або їх порядком, називаються

1) сполуками;

2) подіями;

3) випадковими величинами.

5. Події називають рівноможливими, якщо:

1) немає причин стверджувати, що будь-яка з них можливіша за іншу;

2) поява однієї з них виключає появу інших в одному і тому ж випробуванні;

3) поява однієї з них не виключає появу іншої в одному і тому ж випробуванні.

6. Кількість розміщень з n елементів по k (k≤ n) обчислюють за формулою:

1) ;

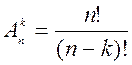2) ;

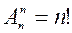3) .

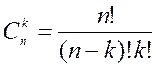7. Що таке ймовірність?

1) число, яке дає кількісну оцінку можливості появи деякої події;

2) це наука, яка вивчає закономірності випадкових явищ;

3) випадкова величина,яка в результаті випробування приймає одне і тільки одне можливе дійсне значення, наперед невідоме і залежне від випадкових обставин.

8. Дві події називаються незалежними, якщо

1) здійснення однієї з них не впливає на ймовірність здійснення іншої;

2) здійснення однієї з них впливає на ймовірність здійснення іншої;

3) ймовірність однієї події обчислена за умови появи іншої події.

9. Ймовірність події В обчислена за умови появи події А називається:

1) умовною ймовірністю;

2) залежною ймовірністю;

3) випадковою ймовірністю.

10. Формула повної ймовірності має вигляд:

1) ;

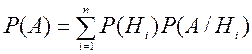2) = ;

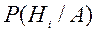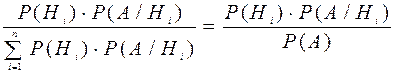3) .

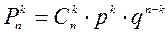Рівень Б

1. Кількість перестановок з n елементів по n обчислюють за формулою:

1) ;

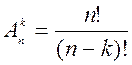2)

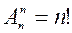
3)

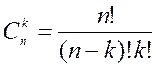
2. Подія: усі студенти І курсу отримають диплом бакалавра є

1) достовірною;

2) випадковою;

3) неможливою.

3. Оберіть неправильне твердження:

1) сума двох протилежних подій – достовірна подія;

2) добуток двох протилежних подій – неможлива подія;

3) сприятливими для різниці подій А і В є елементарні події, які сприятливі і для А і для В.

4. Оберіть правильну тотожність:

1) ;

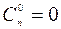2) ;

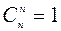3) .

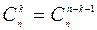5.Якщо елемент а можна вибрати із сукупності елементів m способами, а інший елемент b можна вибрати п способами, то вибрати а або b можна:

1) т+п способами;

2) т·п способами;

3) т–п способами.

6. Якщо події А і В незалежні, то ймовірність добутку цих подій дорівнює

1) добутку їх ймовірностей;

2) добутку ймовірностей однієї з них на умовну ймовірність іншої, за умови, що перша подія відбулася;

3) сумі їх ймовірностей.

7. Сума ймовірностей подій, що утворюють повну групу, не дорівнює:

1) нулю;

2) одиниці;

3) сумі їх ймовірностей.

8. Ймовірність настання принаймні однієї з подій А₁, А₂, ..., А_п , незалежних в сукупності, знаходиться за формулою:

1) ;

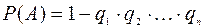2) ;

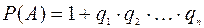3) .

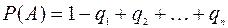9. Чи справедлива тотожність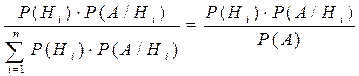

1) так;

2) ні;

10. Аналітичний вираз 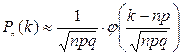має назву

1) формула Пуассона;

2) локальна теорема Муавра – Лапласа;

3) інтегральна теорема Муавра – Лапласа.

Рівень В

1. Студентові треба за 8 днів скласти 4 іспити. Скількома способами це можна зробити? Оберіть правильну формулу для розв’язання задачі

1) ;

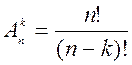2) ;

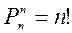3) .

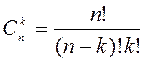2. Скількома способами можна розставити 4 підручники з психології і 3 з педагогіки, щоб всі книжки з педагогіки стояли поряд? Оберіть правильний метод розв’язання

1) перестановки та правило добутку;

2) перестановки та правило суми;

3) комбінації та правило суми.

3. У рибалки є три улюблених місця, куди він приходить з однаковою імовірністю. Імовірність кльову на першому місці дорівнює 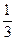, на другому – 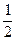, на третьому – 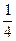. Рибалка закинув вудку у навмання вибраному місці і риба клюнула. Знайти імовірність того, що рибалка закинув вудку у першому місці. Визначте правильну формулу для розв’язання

1) формула Бейєса;

2) формула повної імовірності;

3) формула Бернуллі.

4. У підручнику допущено 50 помилок на 500 сторінках. Яка ймовірність того, що у розділі з 30 сторінок допущено 2 помилки? Визначте правильну формулу для розв’язання

1) формула Пуассона;

2) локальна формула Муавра – Лапласа;

3) інтегральна формула Муавра – Лапласа.

ІІІ. Модульна (аудиторна) контрольна робота передбачає розв’язання по одній задачі з кожного рівня А, Б і В (А–низький – 1б., Б–достатній – 1,5б., В–високий –2,5б.).

Орієнтовні задачі для МКР

Рівень А

1. Гральний кубик підкидають двічі. Описати простір елементарних подій. Описати події: А - сума очок, яка з'явилась, дорівнює 8; В - принаймні один раз з'явиться 6.

2. Монету кинуто двічі. Знайти імовірність того, що хоча б один раз вона впаде гербом вгору.

3. Скількома способами 7 осіб можуть стати в чергу до каси?

4. Десять груп навчаються в десяти аудиторіях, що розміщені поруч. Скільки існує варіантів розміщення груп по аудиторіям, при яких групи №1 і №2 будуть знаходитися в сусідніх аудиторіях?

5. Студентові треба за 10 днів скласти 3 іспити. Скількома способами це можна зробити?

6. Із групи в 15 осіб вибирають чотирьох учасників естафети 800 х 400 х 200 х 100 м. Скількома способами можна розставити спортсменів на етапах такої естафети?

7. Скільки можна утворити різних трицифрових додатних цілих чисел у десятковій системі числення?

8. Скільки треба мати словників, щоб можна було робити переклади з 5-ти мов на будь-яку іншу з них?

9. З урни, що містить 10 чорних та 6 білих куль, вибирають 2 чорні та 3 білі кулі. Скількома способами це можна зробити?

10. Із групи, в яку входять 7 хлопчиків і 4 дівчинки, треба скласти команду із 6 чоловік так, щоб в неї входило не менше 2-х дівчат. Скільки є способів скласти таку команду?

Рівень Б

1. На полиці стоять 2 книжки з філософії, 4 з педагогіки і 3 – з математики. Навмання беруть одну книжку. Визначити ймовірність того, що взята книжка не з математики.

2. Ймовірність перемоги першого спортсмена дорівнює 0,7, другого – 0,8. Знайти ймовірність того, що хоча б однин з них переможе.

3. Між групою студентів із 30 осіб розподілили жеребкуванням путівки для відпочинку: 15 – в Крим, 8 – в Одесу, 7 – у Миргород. Яка ймовірність того, що два друга відпочинуть разом?

4. Студент шукає потрібну йому інформацію на трьох сайтах. Імовірність того, що інформація знаходиться на 1-му, 2-му і 3-тьому відповідно рівна 0,5; 0,7; 0,9. Знайти ймовірність того, що інформація міститься на всіх трьох сайтах.

5. Студент знає 21 із 26 питань програми. Знайти ймовірність того, що студент відповість на 3 питання, запропонованих йому викладачем.

6. Маємо два концентричні кола (мають спільний центр) радіуси яких відповідно рівні R=8, r =4. Знайти ймовірність того, що точка кинута навмання у більше коло не попаде у менше.

7. Три студенти складають іспит з психології. Ймовірність того, що перший складе іспит дорівнює 0,9, для другого – 0,8, для третього – 0,7. Обчислити ймовірність того, що два студенти складуть іспит.

8. Із множини чисел 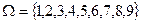беруть навмання одне число, а потім з решти – друге. Яка ймовірність того, що здобуте двоцифрове число буде непарним?

9. Підприємство одержало 20 приймачів, з яких 5 бракованих. Для перевірки навмання взяли три приймача. Яка ймовірність того, що серед взятих приймачів буде один бракований?

10. На автомобілі встановлено два охороні пристрої, які працюють незалежно. Ймовірність того, що при викраденні спрацює переший дорівнює 0,85, другий – 0,95. Знайти ймовірність того, що при викраденні спрацює хоча б один.

Рівень В

1. Ймовірність того, що подія відбудеться хоча б один раз у трьох незалежних випробуваннях дорівнює 0,936. Знайти ймовірність появи події в одному випробуванні, якщо вона однакова у кожному.

2. Із великої зв’язки краваток, в якій краватки зеленого,, червоного і жовтого кольору перебувають у відношенні 5:3:2, двоє чоловіків навмання обирають по одній краватці. Яка ймовірність того, що вони оберуть краватки однакового кольору?

3. Серед студентів п’ятого курсу 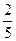одружені а решта неодружені. Серед неодружених студентів 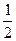молодші 22 років, а 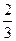одружених старші 22 років. Знайти ймовірність того, що довільно обраний студент цього курсу старший 22 років.

4. У магазин надходять вироби, які виготовляються чотирма фабриками. Ймовірність браку виробів становить 0,04; 0,03; 0,06 і 0,02 відповідно. Від першої фабрики надійшло до магазину 30 виробів, від другої – 20, від третьої – 25, а від четвертої 25 виробів. Знайти ймовірність того, що взятий навмання виріб буде бракований.

5. До центру статистичних досліджень надходить інформація з трьох пунктів: з першого 50%, з другого – 30%, з третього – 20% усієї інформації. Ймовірність допущення помилки при обробці статистичних даних у першому пункті становить 0,1, у другому – 0,05, у третьому – 0,15. Яка ймовірність того, що отримана центром у даний момент часу достовірна інформація надійшла з другого пункту.

6. Ймовірність того, що таксофон відмовиться сприйняти вашу телефонну картку дорівнює 0,2, яка ймовірність того, що з 6 карток буде прийнято 4?

7. Спостереженнями встановлено, що у Полтаві у вересні в середньому буває 12 дощових днів. Яка ймовірність того, що серед навмання взятих у цьому місяці 8 днів три дні виявляться дощовими?

8. У лотереї на кожні 1000 білетів припадає один виграшний. Яка ймовірність того, що володар 200 білетів отримає два виграші.

9. Досліджують 500 проб залізної руди. Ймовірність того, що вміст заліза в ній достатній для промислового використання дорівнює 0,8. Знайти ймовірність того, що кількість таких проб буде від 300 до 400.

10. У перші класи передбачається прийняти 200 дітей. Визначити ймовірність того, що серед них буде 100 дівчат, якщо ймовірність народження хлопчиків у цьому році дорівнює 0,515.

IV. Тема реферату обирається студентом із числа запропонованих. Реферат повинен мати таку структуру: титульна сторінка, план, вступ, основна частина, висновки, список використаних джерел. В основній частині подати коротку біографічну довідку для вченого, але основну увагу приділити науковій діяльності вченого: вказати сфери його наукових досліджень, основні наукові праці, зупинитися на його особистому внеску в розвиток теорії ймовірностей як самостійної науки. Для теми № 15 визначити часові межі зародження теорії ймовірностей як самостійної науки. Виділити окремі етапи розвитку теорії ймовірностей. Окреслити сучасний стан розвитку теорії ймовірностей.

Теми рефератів

1. „Математика випадку” Блеза Паскаля.

2. П. Ферма – творець теорії чисел.

3. Наукові дослідження Г. Гюйгенса в області теорії ймовірностей.

4. Науковий внесок К. Гаусса у теорію чисел.

5. Наукові досягнення А. Лежандра.

6. Теорема Я. Бернуллі як частковий випадок закону великих чисел.

7. С. Пуассон – основоположник теорії ймовірностей

8. Вчення про випадки А. Муавра.

9. Сфера наукових досліджень П. Лапласа.

10. Наукові досягнення Т. Бейєса в теорії ймовірностей.

11. Значення праць П.Л. Чебишова у розвитку теорії чисел.

12. Наукові досягнення А.А. Маркова в області теорії чисел.

13. Метод характеристичних функцій А.М. Ляпунова.

14. Теорія стаціонарних випадкових процесів А.М. Колмогорова.

15. Історія розвитку теорії ймовірностей.

Інформаційні джерела

1. Бородин А.И., Бугай А.С. Выдающиеся математики: Библиографический словарь-справочник. – К.: Рад. школа, 1987. – 653с.

2. Вилейтнер Г. История математики от Декарта до середины XIX столетия. – М.: Наука, 1966

3. Конфорович А.Г. Андриевская А.М. История развития математики: Учеб. нагл. пособие: Альбом. – К.: Вища школа, 1988. – 95 листов.

4. Конфорович А.Г. Колумбы математики. – К.: Рад. школа, 1982. – 223с.

5. Математика XIX века. Математическая логика. Алгебра. Теория чисел. Теория вероятностей. Под ред. А.Н. Колмогорова и А.П. Юшкевича. – М.: Наука, 1978. – 255с.

6. Математический энциклопедический словарь / Гл. ред. Ю.В. Прохоров. – М.: Сов. энциклопедия, 1988. – 845с.

7. Никифоровский В.А. Великие математики. Бернулли. – М.: Наука, 1984. – 177с.

8. Очерки по истории математики: Уч пособие для студентов вузов / Под ред. Б.В. Гнеденко. – М.: МГУ, 1997.- - 496с.

9. Прудников В.Е., Чебышев П.Л. 1821-1894. – Л.: Наука, 1976. – 282с.

10. Рыбников К.А. История математики. – М.: Изд-во Моск. ун-та, 1994. – 496с.

11. Шмигевський М.В. Видатні математики. – Х.: Основа, 2004. – 176с.

12. http:kvant.mirror1.mccmt.ru/1973/08/blez_paskal.htm.

13. http://www.teorver.ru/

14. http://www.math.ru/history/people/Gauss