Практичне заняття №4
Тема: Формула повної ймовірності.
Мета: сформувати та систематизувати знання про проведення незалежних випробувань в рамках одного експерименту, навчити правильно висувати гіпотези про здійснення випадкової події, навчити знаходити ймовірність події за формулою повної ймовірності і ймовірність гіпотези за формулою Бейєса.
Основні знання, якими повинні оволодіти студенти під час вивчення теми: знати формулу повної ймовірності і формулу ймовірності гіпотези (формула Бейєса).
Основні вміння, якими повинні оволодіти студенти під час вивчення теми: вміти правильно висувати гіпотези про здійснення випадкової події, вміти застосовувати формулу повної ймовірності і ймовірності гіпотези при розв’язуванні задач.
План заняття
1. Формула повної ймовірності.
2. Формула ймовірності гіпотези Бейєса.
рекомендована Література
1. Теорія ймовірностей та математична статистика: Навч. посібник для студентів вузів/ В.В. Барковський, Н.В. Барковська Н.В., О.К. Лопатін. 3-є вид. перероб. і доп.– К.: Центр навчальної літератури, 2002. С. 55-68.
2. Математика для психологов: Учебник /А.Н. Киричевец, Е.В. Шикин, А.Г. Дьячков / Под ред. А.Н. Киричевца. – М.:Флинта: Московский психолого-социальный институт, 2003. С. 218-220.
3. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ Н.Ш. Кремер. -3-е изд., перераб. и доп.- М.: Юнити, 2007. – С. 51-67.
4. Теорія ймовірностей...від найпростішого: Навчальний посібник для студентів вузів/ О. Д. Валь, К.С. Королюк, С.В. Мельничук. –Чернівці: Книги-ХХІ, 2004.-С. 39-49.
5. Основи теорії ймовірностей: курс лекцій: Навч. посібник/ В.М. Рабик. – Львів: Магнолія плюс, 2004. С. 30-38.
6. Курс теории вероятностей: Учебник для студентов вузов/ В.П. Чистяков. – 7-е изд., испр. и доп. –М: Дрофа, 2007.- С. 41-46.
7. Теорія ймовірностей: основні поняття, приклади, задачі: Навчальний посібник/ В.М. Турчин. – К.: А.С.К., 2004.- С.35-46.
8. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев. –М.: Даликов и К, 2008. - С.41-50.
9. Теория вероятностей и математическая статистика: Учебное пособие для студентов вузов / Ред. В.И. Єрмаков. –М.: Инфра-М, 2008. –С.20-22.
10. Теория вероятностей и математическая статистика: примеры и задачи: Учебное пособие для студентов вузов/ И.В. Белько, Г.П. Свирид. -3-е изд., стереотип. –М.: Новое знание, 2007. С. 13-27.
11. Посібник з теорії ймовірності та математичної статистики: Навч. посібник для вузів/ М. К. Бугір. – Тернопіль: Підручники і посібники, 1998. –С. 17-32.
12. Основи теорії ймовірностей та математичної статистики: Навчальний посібник для студентів/ В.П. Бабак, А.Я. Білецький, О.П. Приставка, П.О. Приставка.-К.: КВІЦ.,2003. –С.33-35.
13. Прикладные задачи теории вероятности/ Е.С. Вентцель, Л.А. Овчаров. –М.: Радио и связь, 1983. –С.69-81.
14. Математична статистика та задачі оптимізації в алгоритмах і програмах: Навчальний посібник для студентів вузів/ Ю.А.Толбатов. –К.: Вища школа, 1994. –С.11-19.
15. Елементи теорії ймовірностей / В.М. Резанко. Навч. Посібник 3-тє вид., перероб. і доп. – К.: 2006.-С. 36-41.
Методичні вказівки
1. Опрацювати рекомендовану літературу.
2. Повторити означення повної групи подій.
3. Вивчити формулу повної ймовірності, формулу Бейєса і всі позначення в них. Звернути увагу, що гіпотези повинні утворювати повну групу подій.
задачі для самоконтролю
Задача 1.У першому ящику 30 деталей, з яких 20 стандартних. У другому – 15 деталей, з яких 10 стандартних. З ІІ ящика беруть навмання одну деталь і перекладають її до І ящика. Завдання:
а) знайти ймовірність того, що навмання взята після перекладання деталь з І ящика стандартна;
б) нехай відомо, що з І ящика вийнято стандартну деталь, знайти ймовірність того, що до І ящика переклали саме стандартну деталь.
Відповідь: а) 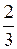 , б)
, б) 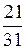 .
.
Задача 2. На фабриці виготовляють гвинти. Перша машина виготовляє 25%, друга – 35%, третя – 40% всіх гвинтів. Частка браку становить відповідно 5%, 4%, 2%. Яка ймовірність того, що випадково вибраний гвинт бракований?
Відповідь: 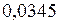 .
.
Задача 3. В урну, що містить 2 кулі, вкинули білу кулю, після чого із урни навмання витягли одну кулю. Знайти ймовірність того, що витягнута куля буде білою, якщо рівноможливі всі передбачення про початковий склад куль по кольору.
Відповідь: 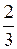 .
.
Задача 4. Ймовірність знищення літака з одного пострілу для І гармати дорівнює 0,2. для ІІ гармати – 0,1. Кожна гармата робить по одному пострілу, причому було одне влучення у літак. Яка ймовірність того, що влучила перша гармата?
Відповідь: 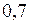 .
.
Дата добавления: 2022-02-05; просмотров: 497;











