Алгебраические структуры и морфизмы.

n-арной операцией на множестве А называется отображение 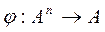, которое каждому упорядоченному набору длины n из элементов множества А сопоставляет некоторый вполне определённый элемент этого же множества.

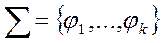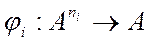Множество А вместе с набором заданных на нём операций , где называется алгебраической структурой 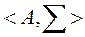или просто алгеброй. При этом множеств А называется носителем структуры, а набор операций 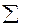- сигнатурой. Чаще всего встречаются операции, арность которой равна 2, бинарные. Таковы, в частности, обычные операции сложения и умножения на числовых множествах. Известными алгебраическими структурами являются группы, кольца, поля.

Подмножество 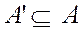называется системой образующих, если любой элемент А может быть получен из А с помощью операций сигнатуры. Так, в алгебре 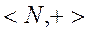натуральных чисел с операцией сложения (полугруппе) один элемент 1 – является образующим, а в алгебре 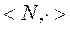натуральных чисел с операцией умножения (моноиде) системой образующих является множество простых чисел и единица.

Пусть имеются две алгебры 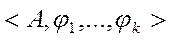и 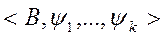, причем арность соответствующих операций одинакова.

Определение. Отображение 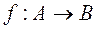называется гомоморфизм из A в B , если оно сохраняет все операции сигнатуры, то есть 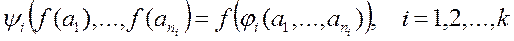. Если f - биекция, то гомоморфизм называется изоморфизмом.

С алгебраической точки зрения изоморфные алгебраические структуры неразличимы. Примером изоморфизма алгебраических структур является алгебра 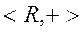множества действительных чисел с операцией сложения (группа) и алгебра 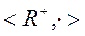положительных действительных чисел с операцией умножения (группа). Биективным отображением 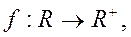устанавливающим изоморфизм является функция 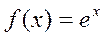, так как 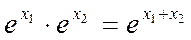. На данном изоморфизме основано, в частности, выполнение умножения с помощью логарифмической линейки, так как обратное отображение 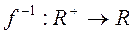задается логарифмической функцие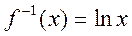й и .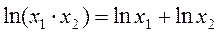

В качестве примера гомоморфизма алгебраических структур, не являющегося изоморфизмом, можно привести алгебру квадратных матриц заданного порядка n над полем действительных чисел с операцией умножения матриц (моноид) и алгебру действительных чисел с операцией умножения (моноид). Отображением, задающим гомоморфизм из множества матриц в множество чисел, является операция вычисления определителя квадратной матрицы: .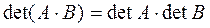

Гомоморфизм называется:

- мономорфизмом, если f - инъекция;

- эпиморфизмом, если f - сюръекция;

- эндоморфизмом, если f - отображает носитель

структуры на себя;

- автоморфизмом, если f - биективный эндоморфизм.

Примером автоморфизма группы является операция сопряжения с помощью фиксированного элемента 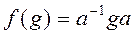, так как .

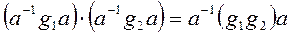Пусть задана некоторая алгебраическая структура 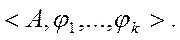Отношение эквивалентности R на множестве A называется отношением конгруэнтности, если оно согласовано со всеми операциями сигнатуры в следующем смысле:

из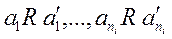

следует 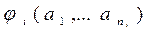R .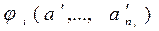

Другими словами, класс эквивалентности, в который попадает результат любой операции сигнатуры, полностью определяется классами, из которых берутся аргументы операции.