Дизъюнктивная и конъюнктивная нормальные формы
Пусть 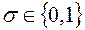 , будем считать, что
, будем считать, что 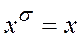 , если
, если 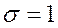 и
и 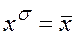 , если
, если 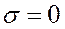 .
.
Конъюнкция и дизъюнкция являются ассоциативными операциями: 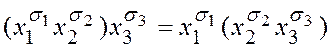 и
и 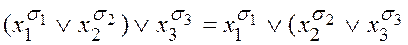 ). Поэтому определены выражения
). Поэтому определены выражения 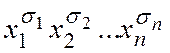 и
и 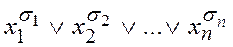 , которые называются элементарной конъюнкцией и элементарной дизъюнкцией длины n соответственно. Заметим, что конъюнкция принимает значение 1 на единственном наборе значений переменных
, которые называются элементарной конъюнкцией и элементарной дизъюнкцией длины n соответственно. Заметим, что конъюнкция принимает значение 1 на единственном наборе значений переменных 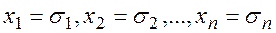 , а на всех остальных наборах значений переменных обращается в 0. Дизъюнкция же, напротив, принимает значение 0 на единственном наборе значений переменных , а на всех остальных наборах значений переменных равна 1.
, а на всех остальных наборах значений переменных обращается в 0. Дизъюнкция же, напротив, принимает значение 0 на единственном наборе значений переменных , а на всех остальных наборах значений переменных равна 1.
Это позволяет каждую булеву функцию представить в виде
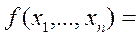
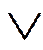
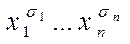
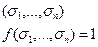

или в виде
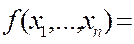 &
& 
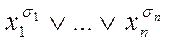
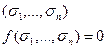
которые называются соответственно совершенной дизъюнктивной нормальной формой (д.н.ф.) и совершенный конъюнктивной нормальной формы (к.н.ф.) для функции ƒ.
В совершенных д.н.ф. и к.н.ф. все элементарные конъюнкции (э.к.) и элементарные дизъюнкции (э.д.) имеют одинаковую длину, равную числу переменных n. Может, однако, оказаться, что у некоторых э.к. в совершенной д.н.ф. может быть опущена часть букв, а другие э.к. могут быть одновременно вообще удалены, причем полученная д.н.ф. (уже не сокращенная) будет представлять ту же самую функцию . Тем самым иногда удается существенно упростить представление булевой функции в виде д.н.ф.. Аналогично может быть упрощена и к.н.ф.. В процессе упрощения могут использоваться свойства 1) – 9) булевой алгебры.
Упрощение д.н.ф.
Рассмотрим схему упрощения д.н.ф. подробнее. Э.к. называется импликантом функции ƒ, если она равна 0 на всех наборах значений переменных, на которых равна 0 функция ƒ. Импликант называется простым, еcли при удалении из него любой буквы он перестает быть импликантом. Все простые импликанты функции ƒ могут быть получены из конъюнкций её совершенный д.н.ф. удалением некоторых из переменных. Д.н.ф., составленная из всех простых импликантов функции f, реализуем функцию f. Некоторые из э.к. этой д.н.ф. можно удалить, придя, в конце концов, к д.н.ф., из которой нельзя удалить ни одной э.к., не изменив реализуемую функцию. На этом процессе упрощение заканчивается.
Заметим здесь, что выбор удаляемых простых импликантов не однозначен и различные выборы могут привести к различным заключительным д.н.ф. Однако для монотонной булевой функции данная схема упрощения приводит к единственной д.н.ф. Простые импликанты монотонной булевой функции не содержат отрицаний переменных и ни один из них не может быть удален.
Рассмотрим схему упрощения д.н.ф. на примере. Пусть булева функция от трех переменных 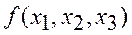 задана таблицей
задана таблицей
| х1 | х2 | х3 | f(х1 ,х2, х3) |
Тогда совершенная д.н.ф. запишется в виде:
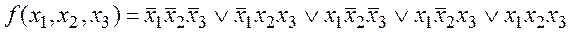
Найдем пары э.к., различающиеся лишь в одной букве так, что в одну э.к. эта буква входит с отрицанием, а в другую – без отрицания. Затем, воспользовавшись свойствами булевой алгебры, заменим каждую из пар одной э.к., не содержащей данной буквы (слияние пар).
Парами с требуемыми свойствами будут
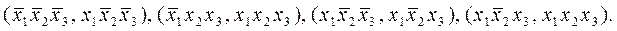
Заменив каждую из пар одной конъюнкцией, получаем
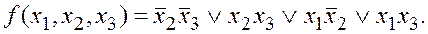
В полученной д.н.ф. нет ни одной пары э.к., с которой можно было бы выполнить операцию слияния. Это говорит о том, что все импликанты в данной д.н.ф. – простые.
Теперь можно попытаться удалить некоторые из импликантов. Это легче всего сделать с помощью таблицы, строки которой соответствуют наборам значений переменных, на которых функция равна 1, а столбцы простым импликантам. В клетках таблицы ставится 1,если простой импликант принимает значение 1 на данном наборе, и 0 – в противном случае.
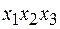
| 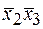
| 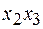
| 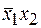
| 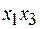
|
| 0 0 0 | ||||
| 0 1 1 | ||||
| 1 0 0 | ||||
| 1 0 1 | ||||
| 1 1 1 |
В каждой строке таблицы содержится хотя бы одна единица. это выражает тот факт, что д.н.ф., составленная из всех простых импликантов, представляет функцию f. Задача состоит в выборе минимального числа столбцов, сохраняющего данное свойство. Считая, что каждый столбец покрывает те строки, в которых он содержит 1, данную задачу можно сформулировать как задачу о минимальном покрытии строк столбцами.
Из таблицы видно, что первая строка покрывается только первым столбцом, а вторая – вторым. Поэтому первый и второй столбец обязательно входят в покрытие.
После того, как они берутся в покрытие, непокрытой остается лишь четвертая строка, которая может быть покрыта пустым или четвертым столбцом. Это дает две простейшие д.н.ф., представляющие функцию f:
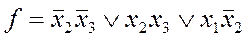 и
и
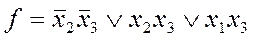 .
.
Процессу нахождения простейшей д.н.ф. может быть дана изящная геометрическая интерпретация в терминах вершин, ребер и граней единого куба. Набором значений переменных ставятся в соответствии вершины куба, а каждой э.к. ставится в соответствии множество вершин, на которых она обращается в 1. Трехбуквенным э.к. соответствуют вершины куба, двухбуквенным - его грани, однобуквенным – ребра.
На рисунке отмечены единые вершины функции f и ребра, соответствующие простым импликантам.
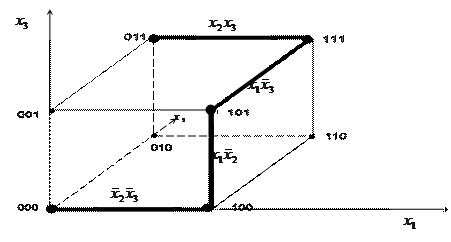 |

Выпишем теперь для функции f(х1, х2, х3) совершенную к.н.ф.:
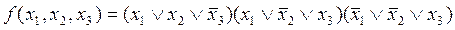 и перемножим скобки, воспользовавшись дистрибутивным свойством алгебры
и перемножим скобки, воспользовавшись дистрибутивным свойством алгебры
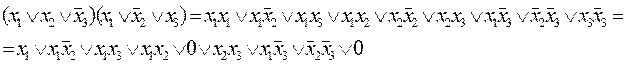
Согласно закону поглощения
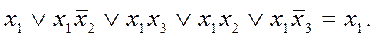
Поэтому окончательно произведение двух первых скобок равно 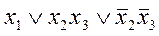 . Умножая это выражение на последнюю скобку, получаем
. Умножая это выражение на последнюю скобку, получаем
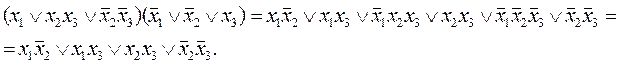
Это есть еще один способ получения всех простых импликантов функции f.
Контрольные вопросы.
1. Какую функцию называют булевой?
2. Какое множество является областью определения и областью значений булевой функции?
3. Какие 3 операции над булевыми функциями задают булеву алгебру?
4. Дайте определение д.н.ф. и к.н.ф.
5. Опишите механизм упрощения д.н.ф.
Тест III
1. Булевой функцией от n переменных называется функция, определенная на множестве всех двоичных наборов длины n и принимающая на каждом из них значение.
а) 0; б) 1; в) 0 или 1; г) любые целые;
2. Булева функция называется монотонной, если из х 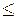 у следует
у следует
а) 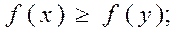 б)
б) 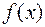 >
> 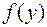 ; в)
; в) 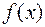
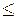
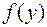 ; г)
; г) 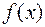 <
< 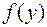 ;
;
3. Выражение 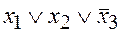 называют
называют
а) элементарной дизъюнкцией; б) элементарной конъюнкцией.
4. Результатом упрощения д.н.ф. 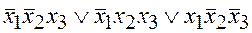 является форма:
является форма:
а) 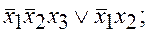 б)
б) 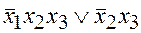 ; в)
; в) 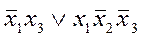 .
.
5. Функцией, двойственной к функции 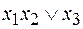 , является
, является
а) 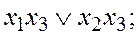 б)
б) 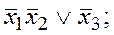 в)
в) 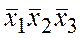
Дата добавления: 2022-02-05; просмотров: 579;











