Определение и основные свойства.
Булевой или логической функцией от n переменных 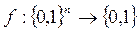 называется функция
называется функция 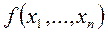 , определенная на множестве всех двоичных наборов длины n и принимающая на каждом из них значение 0 или 1. Так как двоичных наборов длины n имеется 2n , то булевых функций от n переменных
, определенная на множестве всех двоичных наборов длины n и принимающая на каждом из них значение 0 или 1. Так как двоичных наборов длины n имеется 2n , то булевых функций от n переменных 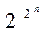 . Булевы функции играют важную роль в логике, а также при проектировании различных логических кибернетических устройств, например, электронных вычислительных машин. Так как область изменения каждой переменной и область значений функции есть одно и то же множество
. Булевы функции играют важную роль в логике, а также при проектировании различных логических кибернетических устройств, например, электронных вычислительных машин. Так как область изменения каждой переменной и область значений функции есть одно и то же множество 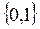 , то это позволяет вместо каждой из переменных некоторой функции подставлять другие функции, получая, таким образом, из имеющегося запаса функций новые функции.
, то это позволяет вместо каждой из переменных некоторой функции подставлять другие функции, получая, таким образом, из имеющегося запаса функций новые функции.
Булевы функции от одной переменной f(x) четыре: 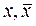 (не x) и тождественные 0 и 1 .
(не x) и тождественные 0 и 1 .
Булевых функций от 2 переменных 16 .
Перечислим важнейшие из них;
- конъюнкция (логическое ,,И”), обозначаемая 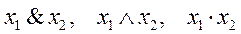 или просто
или просто 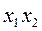 ;
;
- дизъюнкция (логическое ,,ИЛИ”) 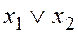 ;
;
- импликация (следование) 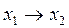 ,
,
- эквивалентность 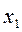 ~
~ 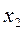 .
.
Приведем таблицу, задающую 4 указанных функции (таблицу истинности):
 x1 x2 x1 x2
| x1x2 | x1 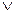 x2 x2
| x1®x2 | x1~x2 |
| 0 0 | ||||
| 0 1 | ||||
| 1 0 | ||||
| 1 1 |
Заметим, что 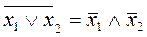 и
и 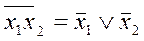 , то есть выполнены законы де Моргана. Вообще, булевой функции от переменных можно поставить в соответствие подмножество тех двоичных наборов, на которых она равна 1. Тем самым устанавливается изоморфизм между множеством подмножеств 2n - элементного множества с операциями объединения, пересечения и дополнения и множеством булевых функций от n переменных с операциями дизъюнкции, конъюнкции и отрицания. Поэтому множество булевых функций от n переменных с тремя перечисленными операциями является булевой алгеброй со всеми вытекающими отсюда свойствами.
, то есть выполнены законы де Моргана. Вообще, булевой функции от переменных можно поставить в соответствие подмножество тех двоичных наборов, на которых она равна 1. Тем самым устанавливается изоморфизм между множеством подмножеств 2n - элементного множества с операциями объединения, пересечения и дополнения и множеством булевых функций от n переменных с операциями дизъюнкции, конъюнкции и отрицания. Поэтому множество булевых функций от n переменных с тремя перечисленными операциями является булевой алгеброй со всеми вытекающими отсюда свойствами.
Заметим, что импликация и эквивалентность могут быть выражены через дизъюнкцию конъюнкцию и отрицание
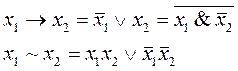
что непосредственно может быть проверено с помощью таблицы истинности.
Кроме того, эквивалентность может быть выражена через импликацию следующим образом

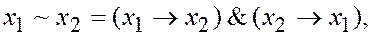
что вполне отвечает привычному представлению о том, что х1 эквивалентно х2, если х1 влечет х2 и х2 влечет х1.
Булева функция 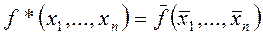 называется двойственной к функции f(x,..., xn), f**=f. Если f*=f , то f называется самодвойственной. Дизъюнкция и конъюнкция двойственны друг другу.
называется двойственной к функции f(x,..., xn), f**=f. Если f*=f , то f называется самодвойственной. Дизъюнкция и конъюнкция двойственны друг другу.
На множестве двоичных наборов длины n отношение порядка
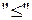 вводится следующим образом:
вводится следующим образом:
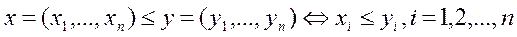
Если считать наборы характеристическими векторами подмножеств n-элементного множества, то это отношение на множестве наборов соответствует упорядоченью подмножеств по включению.
Булева функция f называется монотонной, если из 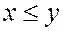 следует
следует 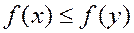 .
.
Дата добавления: 2022-02-05; просмотров: 581;











