Алгебраические и трансцендентные функции
В множестве элементарных функций выделяют алгебраические и трансцендентные функции.
Алгебраическими функцияминазывают целые многочлены, рациональные дроби и иррациональные функции.
Например, 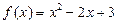 ;
; 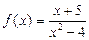 ;
; 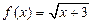 .
.
Трансцендентными функцияминазывают элементарные функции, не являющиеся алгебраическими.
Например, 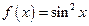 ;
; 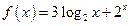 ;
; 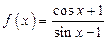 .
.
Среди алгебраических функций выделяются целые многочлены и рациональные дроби.
Целым многочленом (полиномом)степени n относительно переменной x называется функция следующего вида:
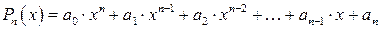 (1)
(1)
здесь 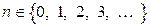 — степень многочлена;
— степень многочлена;
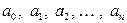 – коэффициенты многочлена (числа или параметры);
– коэффициенты многочлена (числа или параметры);
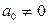 – старший коэффициент.
– старший коэффициент.
Примеры (целые многочлены)
1) 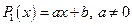 – многочлен первой степени;
– многочлен первой степени;
2) 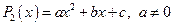 — квадратный трехчлен, или квадратичная функция;
— квадратный трехчлен, или квадратичная функция;
3) 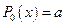 — многочлен нулевой степени;
— многочлен нулевой степени;
4) 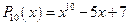 - многочлен 10-й степени.
- многочлен 10-й степени.
График квадратичной функции
Функция 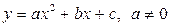 называется квадратичной функцией.
называется квадратичной функцией.
Число 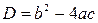 называется дискриминантом квадратного трехчлена.
называется дискриминантом квадратного трехчлена.
Графиком квадратичной функции является парабола, ее положение относительно координатных осей определяется знаком старшего коэффициента a и значением дискриминанта D (см. таблицу на рис. 59).
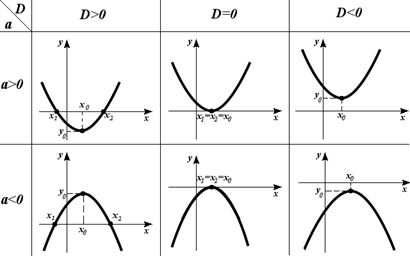
Рис.59
Здесь x1, x2 — это нули квадратичной функции,
вычисленные как корни квадратного уравнения 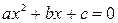 Þ
Þ 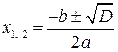 , если
, если 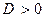 ;
;
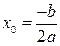 — абсцисса вершины параболы (точка экстремума);
— абсцисса вершины параболы (точка экстремума);
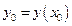 — ордината вершины (экстремум квадратичной функции).
— ордината вершины (экстремум квадратичной функции).
Иррациональные функции— это такие алгебраические функции 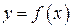 , у которых выражение
, у которых выражение 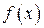 содержит корни различных степеней.
содержит корни различных степеней.
Например, 1) 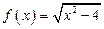 ; 2)
; 2) 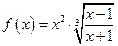 ; 3)
; 3) 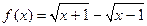 .
.
Рациональные дроби
Рациональной дробью (рациональной функцией)называется функция, записанная как отношение двух целых многочленов:
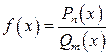 , (2)
, (2)
где 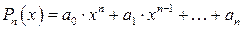 ,
, 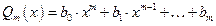 .
.
Например,
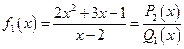 ;
; 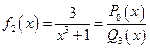 ;
; 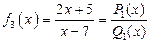 .
.
Рациональная функция (2) называется правильной рациональной дробью, если степень многочлена в числителе меньше степени многочлена в знаменателе, то есть если 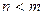 , и называется неправильной рациональной дробью, если степень многочлена в числителе больше или равна степени многочлена в знаменателе, то есть если
, и называется неправильной рациональной дробью, если степень многочлена в числителе больше или равна степени многочлена в знаменателе, то есть если 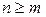 .
.
Например, в предыдущем примере: 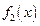 — правильная рациональная дробь,
— правильная рациональная дробь,
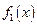 и
и 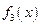 — это неправильные рациональные дроби.
— это неправильные рациональные дроби.
Делением многочлена на многочлен «в столбик» любую неправильную рациональную дробь можно представить в виде суммы целого многочлена и правильной рациональной дроби. Эта процедура называется выделением целой части в неправильной рациональной дроби.
Примеры (выделение целой части в неправильной рациональной дроби)
1) 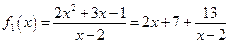 , ,
| так как | 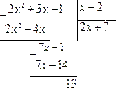
|
2) 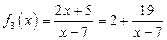 , ,
| так как | 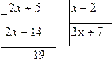
|
Простейшими (элементарными) рациональными дробяминазываются следующие правильные дроби вида I-IV:
I. 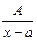 II.
II. 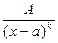 , k = 2, 3… , k = 2, 3…
| III. 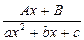 ,
IV. ,
IV. 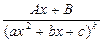 , k = 2, 3,… , k = 2, 3,…
|
при этом D = b2 – 4ac < 0, так что уравнение ax2 + bx + c = 0 не имеет корней на 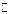 . .
|
Справедливо следующее важное свойство правильных рациональных дробей.
| Свойство (о разложении правильной рациональной дроби на сумму простейших дробей) |
Любую правильную рациональную дробь можно единственным образом представить в виде суммы простейших дробей вида I, II, III, IV.
Для этого нужно:
1) многочлен в знаменателе правильной рациональной дроби разложить на произведение линейных и квадратичных сомножителей с действительными коэффициентами;
2) записать простейшие дроби для каждого множителя знаменателя:
для простого множителя 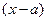 записать дробь вида I : записать дробь вида I : 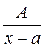 для кратного линейного множителя
для кратного линейного множителя 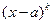 записать сумму записать сумму 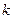 дробей вида I и дробей вида I и
 II :
для квадратичного множителя
II :
для квадратичного множителя 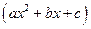 записать дробь вида III: записать дробь вида III:
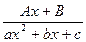 ;
для кратного квадратичного множителя ;
для кратного квадратичного множителя 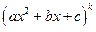 записать сумму записать сумму  дробей вида III, IV: дробей вида III, IV: 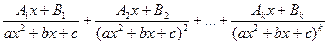 ;
3) неопределённые коэффициенты в числителях простейших дробей ;
3) неопределённые коэффициенты в числителях простейших дробей 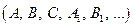 найти из условия тождественного равенства исходной дроби и записанной суммы простейших дробей. найти из условия тождественного равенства исходной дроби и записанной суммы простейших дробей.
|
Примеры (разложение правильных рациональных дробей на сумму
простейших дробей)
1) 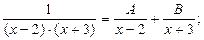
2) 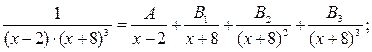
3) 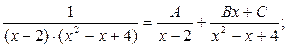
4) 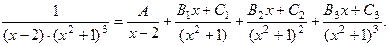
Вычислим неопределенные коэффициенты в разложениях 1) и 3):
1) 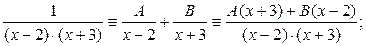
так как тождественно равны две дроби с одинаковыми знаменателями, то тождественно равны их числители:
1 º A(x + 3) + B(x – 2); (*)
вычисляем числа А и В, используя метод частных значений x, суть которого состоит в следующем: тождественное равенство двух многочленов относительно x означает, что равны значения этих многочленов при любых частных значениях x;
в рассматриваемом примере удобными частными значениями x являются x = 2 и x = -3. подставим эти значения x в последнее равенство (*):
при x = 2 получим 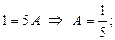
при x = –3 получим 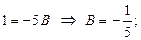
вычислив неопределенные коэффициенты, обязательно нужно делать проверку получившемуся разложению:
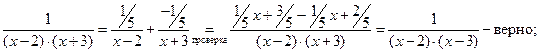
таким образом, неопределенные коэффициенты вычислены верно, и разложение правильной рациональной дроби на простейшие дроби имеет вид:
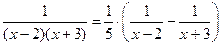 ;
;
3) 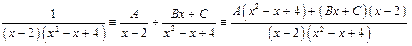
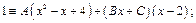
для нахождения чисел А, В, С можно также использовать способ приравнивания коэффициентов при одинаковых степенях x, который основан на следующем свойстве целых многочленов: тождественное равенство двух многочленов означает совпадение их коэффициентов при одинаковых степенях x;
в рассматриваемом примере в последнем равенстве справа раскроем скобки и приведем подобные по x:
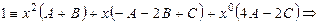
| приравниваем коэффициенты при x2: | 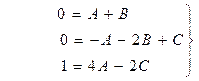
|
| приравниваем коэффициенты при x1: | |
| приравниваем коэффициенты при x0: |
в результате получилась система трёх линейных уравнений относительно трёх неизвестных А, В, С. Решаем эту систему:
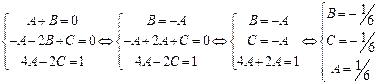
таким образом, неопределенные коэффициенты вычислены. Подставляем их в искомое разложение и обязательно делаем проверку:
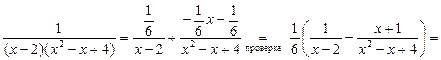
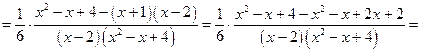
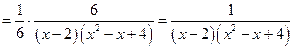 — верно.
— верно.
Ответ: 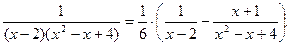
Дата добавления: 2021-07-22; просмотров: 722;











