Бинарные отношения.

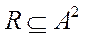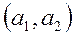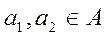Пусть A - множество. Если задано некоторое подмножество его декартового квадрата, другими словами, задано некоторое подмножество упорядоченных пар , где , то говорят, что на множестве A задано бинарное отношение R. Пишут 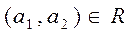или 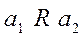.В качестве примеров бинарных отношений на числовых множествах можно рассмотреть хорошо известные из арифметики отношения: ,,=”, ,,<”, ,,£”, ,,>”, ,,³”.

Бинарное отношение называется:

- рефлексивным, если для любого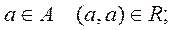

- иррефлексивным, если для любого ;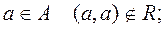

- симметричным, если из 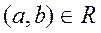следует ;

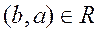- антисимметричным, есл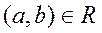и и 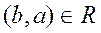следует a=b;

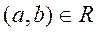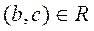- транзитивным, если из и следует ;

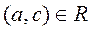Отношение ,,=” рефлексивно, симметрично и транзитивное, отношения ,,<” и ,,>” транзитивны и иррефлексивны, отношения ,,£” и ,,³”. рефлексивны, антисимметричны и транзитивны. Последние свойства выбираются в качестве определяющих для отношения частичного порядка на множестве A.

Определение. Бинарное отношение R на множестве A называется отношением частичного порядка, если оно рефлексивно, антисимметрично и транзитивно,

Если 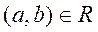, то будем считать элемент a предшествующим элементу b и записывать отношение aRb в виде 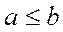. Если для любых двух 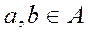элементов имеет место хотя бы одно из отношени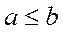й или 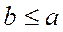, то частичный порядок называется полным или линейным порядком.

Примером частичного порядка является система множеств, упорядоченных по включению: 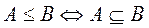. Числовые множества с обычным отношением ,, £” дают примеры линейных порядков.

Пусть <A, £ > - частично упорядоченное множество. Элемент 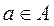называется минимальным, если из 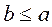следует 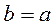. Минимальных элементов может быть больше одного. Элемент 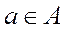называется наименьшим, если 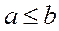для любого 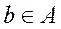. Если в A имеется наименьший элемент, то он единственен. Аналогично определяются максимальный и наибольший элемент.

Обобщением понятия равенства является отношение эквивалентности.

Определение. Бинарное отношение R на множестве A называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Отношение эквивалентности разбивает множество A на непересекающиеся подмножества, называемые классами эквивалентности. Если в качестве A рассмотреть множество людей, проживающих в домах некоторого города, то отношение проживания в одном доме будет отношением эквивалентности. Более математическим примером является отношение сравнения по модулю n в множестве целых чисел Z: 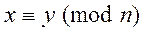, если 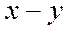делится на n. При этом Z разбивается на классы 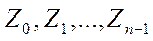, характеризуемые остатками от деления на n. Более общим примером является эквивалентность элементов группы G по подгруппе H: 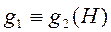если 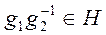. Классами эквивалентности здесь являются правые смежные классы по подгруппе H.

Функции.

Если каждому элементу множества A поставлен в соответствии единственный элемент множества B, то говорят, что задано отображение из A в B или функция 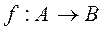. Если 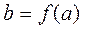, то элемент a называется образом элемента b , а b -прообразом элемента a.

Функция f называется:

- инъекцией, если из 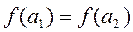следует ;

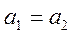- сюръекцией, если для каждого 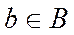существует 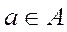такой, что ;

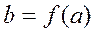- биекцией, если f является инъекцией и сюръекцией одновременно.

Для биекции f можно определить обратную функцию 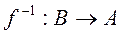. Примерами прямой и обратной функций в математическом анализе является 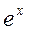и ln x, sin x и arcsin x, x² и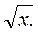

Если на множествах A и B определены отношения частичного порядка, то функция 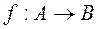называется монотонной, если из 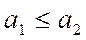следует .

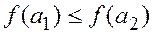Пусть 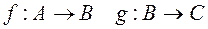. Тогда можно определить композицию функций g ● 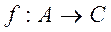, при которой образом элемента 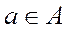является 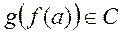. В курсе математического анализа подобную функцию называют сложной функцией.

Множество всех биекций из A в A с операцией композиции образует группу. Если A -конечное n-элементное множество, то это S_n -симметрическая группа степени n.