Отношение конгруэнтности позволяет определить так называемую фактор-структуру, носителем которой является множество классов эквивалентности. Приведём примеры.
Пусть 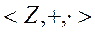 - алгебраическая структура целых чисел с операциями сложения и умножения. Отношение сравнения по модулю n является отношением конгруэнтности и позволяет определить фактор-структуру
- алгебраическая структура целых чисел с операциями сложения и умножения. Отношение сравнения по модулю n является отношением конгруэнтности и позволяет определить фактор-структуру 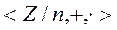 , элементами которой являются классы вычетов
, элементами которой являются классы вычетов 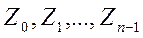 . Она называется кольцом классов вычетов по модулю n .
. Она называется кольцом классов вычетов по модулю n .
Отношение эквивалентности элементов группы G по нормальной подгруппе H является отношением конгруэнтности и позволяет определить на множестве смежных классов фактор-группу G/H .
Контрольные вопросы
1.Дайте определение бинарного отношения.
2.Какое бинарное отношение называют транзитивным?
3.Приведите пример бинарного отношения.
4.Какое бинарное отношение называют отношением эквивалентности?
5.Что называют функцией?
Тест II
1.На множестве А={1,3,5,7} задано бинарное отношение R={(x,y):x-y=4}. Какая из пар принадлежит данному отношению?
а) (1,3); б) (3,7); в) (5,1).
2.Какими свойствами обладает отношение “х делит у” на множестве N ?
| а) рефлексивность, | б) рефлексивность, | в) только рефлексивность. |
| симметричность, | антисимметричность, | |
| транзитивность; | транзитивность; |
3.Элемент 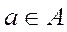 называется минимальным, если из
называется минимальным, если из 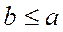 следует, что
следует, что
а) b<a; б) 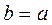 ; в) a<b.
; в) a<b.
4. Если из 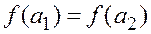 следует а1=а2, то функцию называют
следует а1=а2, то функцию называют
а) инъекцией; б) сюръекцией; в) биекцией.
5. Является ли функция 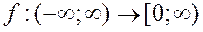 , где f (x)=x2
, где f (x)=x2
а) инъекцией; б) сюръекцией; в) биекцией.
Дата добавления: 2022-02-05; просмотров: 567;











