Операции над множествами.

Множества. Определения и обозначения.

Множество – это собрание определённых и различимых между собой объектов, мыслимых как единое целое. Объекты, называемые элементами множества, могут иметь физическую природу (яблоки, песчинки, люди, звёзды) или быть продуктом нашего интеллекта (числа, фигуры, буквы).

Множества обозначаются большими латинскими буквами А ,В, С, ..., а их элементы – малыми буквами, обычно одноимёнными. Запись А={a₁,...,a_n} означает, что множество А состоит из элементов a₁,...,a_n. Запись aÎА означает, что элемент a принадлежит множеству А. Множество, не содержащее ни одного элемента, называется пустым и обозначается Æ . Запись В А означает, что множество В является подмножеством множества А, т. е. каждый элемент множества В является элементом множества А. Само множество А и Æ называются несобственными подмножествами множества А, все остальные подмножества – собственные.

Операции над множествами.

Множество, состоящее из элементов, входящих хотя бы в одно из множеств А или В, называются объединением множеств А и В и обозначается АÈ В.

Множество, состоящее из элементов, входящих в оба множества А и В, называются пересечением множеств А и В и обозначается А Ç В.

Множество, состоящее из элементов, входящих в А, но не входящих в В, называется разностью множеств А и В и обозначается А\В.

Если имеется некоторое универсальное множеств V такое, что все рассматриваемые множества являются его подмножествами, то может быть введена операция дополнения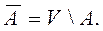

Операции над множествами могут быть наглядно представлены с помощью диаграмм Эйлера-Венна:

	V   ФА		V

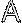
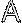
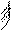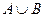
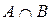
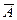
1.3. Свойства операций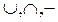

Операции 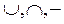производимые над подмножествами некоторого множества V, обладают следующими свойствами:

1. A ÈA=A, AÇA=A -идемпотентность

2. AÈB=BÈA, AÇB=BÇA -коммутативность

3. (AÈB) ÈC=AÈ (BÈ C),

(AÇB) ÇC=AÇ(BÇC) -ассоциативность

4. AÈ(AÇB)=A, AÇ (AÈB)=A -поглощение

5. AÇ(BÈC)=(AÇB)È(AÇC),

AÈ(BÇC)=(AÈB) Ç (AÈC) -дистрибутивность

6. AÇ 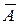=Æ, AÇÆ=Æ AÈÆ=A -закон нуля

7. AÈ 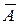=V, AÈV=V, AÇV=A -закон единицы

8. 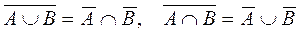-правило де Моргана

9. 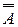=A -инволютивность.

Заметим, что система свойств не изменяется, если одновременно поменять местами операции È и Ç и множества Æ и V. Это есть проявление так называемого принципа двойственности.

Любая структура с 3 операциями, обладающими перечисленными свойствами, называется булевой алгеброй. Множество подмножеств множества V с операциями 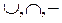образует, следовательно, булеву алгебру.

Отметим, что, если 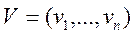- конечное n – элементное множество, то любое его подмножество 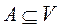может быть задано с помощью двоичного набора .

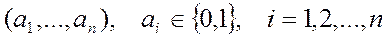При этом 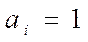означает, что 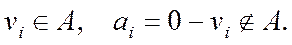Набор 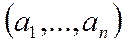называется характеристическим вектором множества А.