Локальная теорема Муавра-Лапласа.
Теорема Муавра-Лапласа устанавливает условия, при которых биномиальную случайную величину можно приближённо рассматривать как нормальную.
Пусть X~B(n, p). При n®¥ и любых фиксированных a и b, a£b:
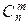 pmqn-m~
pmqn-m~ 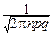 exp[-
exp[- 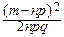 ] *)
] *)
для любых m, удовлетворяющих неравенствам: a£ 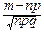 £b.
£b.
Ошибка приближения зависит от того, достаточно ли велико n, не слишком ли близко p к 0 или к 1 и каково интересующее нас значение m. Эта ошибка в настоящее время хорошо изучена и оценена; при необходимости всю нужную информацию можно найти в литературе.
Интегральная теорема Муавра-Лапласа.
Пусть X~B(n, p). Тогда при n®¥ и любых фиксированных a и b, a£b:
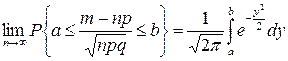
Теорема Муавра-Лапласа позволяет уточнить связь относительной частоты и вероятности.
По этой формуле можно приближённо находить вероятность a заданного отклонения относительной частоты от вероятности, вычислять необходимое число опытов n, при котором с данной вероятностью a указанное отклонение не превышает e. Исходное уравнение выглядит так: 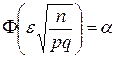 .
.
Дата добавления: 2022-02-05; просмотров: 375;











