ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ

Методы обработки ЭД опираются на базовые понятия теории вероятностей и математической статистики. К их числу относятся понятия генеральной совокупности, выборки, эмпирической функции распределения.

Под генеральной совокупностью понимают все возможные значения параметра, которые могут быть зарегистрированы в ходе неограниченного по времени наблюдения за объектом. Такая совокупность состоит из бесконечного множества элементов. В результате наблюдения за объектом формируется ограниченная по объему совокупность значений параметра x₁, x₂, …, x_n. С формальной точки зрения такие данные представляют собой выборку из генеральной совокупности. Наблюдаемые значения x_i называют вариантами, а их количество – объемом выборки n. Для того чтобы по результатам наблюдения можно было делать какие-либо выводы, выборка должна быть репрезентативной (представительной), т. е. правильно представлять пропорции генеральной совокупности. Это требование выполняется, если объем выборки достаточно велик, а каждый элемент генеральной совокупности имеет одинаковую вероятность попасть в выборку.

Пусть в полученной выборке значение x₁ параметра наблюдалось n₁ раз, значение x₂ – n₂ раз, значение x_k – n_k раз, n₁ + n₂ + … + n_k= n. Совокупность значений, записанных в порядке их возрастания, называют вариационным рядом, величины n_i – частотами, а их отношения к объему выборки n_i = n_i / n – относительными частотами (частостями). Очевидно, что сумма относительных частот равна единице. Другой формой вариационного ряда является ряд накопленных частот, называемый кумулятивным рядом.

Под распределением понимают соответствие между наблюдаемыми вариантами и их частотами или частостями. Пусть n_x – количество наблюдений, при которых случайные значения параметра Х меньше x. Частость события X<x равна n_x / n. Это отношение является функцией от x и от объема выборки: F_n(x)= nx / n. Величина F_n(x) обладает всеми свойствами функции распределения:

· F_n(x) – неубывающая функция, ее значения принадлежат отрезку [0 – 1];

· если x₁ – наименьшее значение параметра, а x_k – наибольшее, то F_п(x)=0, когда x<=x₁, и F_п(x)=1, когда x>x_k .

Функция F_п(x) определяется по ЭД, поэтому ее называют эмпирической функцией распределения. В отличие от эмпирической функции F_n(x) функцию распределения F(x) генеральной совокупности называют теоретической функцией распределения, она характеризует не частость, а вероятность события X<x. Из теоремы Бернулли вытекает, что частость F_n(x) стремится по вероятности к вероятности F(x) при неограниченном увеличении n. Следовательно, при большом объеме наблюдений теоретическую функцию распределения F(x) можно заменить эмпирической функцией F_n(x).

Основные свойства функции F_n ( x).

1. 0 F_n(x) 1.

2. F_n (x) - неубывающая ступенчатая функция.

3. F_n(x) = 0, x x₁ .

4. F_n(x) = 1, x > x_n .

Пример 2.1 Задана выборка случайной величины X: {4 3 3 5 2 4 3 4 4 5}. Построить график эмпирической функции распределения F_n(x).

Решение. Вариационный ряд случайной величины имеет вид {2 3 3 3 4 4 4 4 5 5}. Затем выделяем полуинтервалы (-,2], (2,3], (3,4], (4,5], (5,+]. На полуинтервале (-,2] F_n(x)=0/10=0. При 2<x3 F_n(x)=1/10=0,1.

Аналогично определяем значения F_n(x) на остальных полуинтервалах:

.

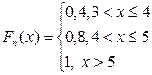График функции F_n(x)приведен на рис. 2.1.

Замечание. В каждой точке оси x, соответствующим значениям xi функция F_n(x) имеет скачок. В точке разрыва F_n(x) непрерывна слева и принимает значение, выделенное знаком .

ГИСТОГРАММА

При большом объеме выборки (понятие «большой объем» зависит от целей и методов обработки, в данном случае будем считать n большим, если n>40) в целях удобства обработки и хранения сведений прибегают к группированию ЭД в интервалы. Количество интервалов следует выбрать так, чтобы в необходимой мере отразилось разнообразие значений параметра в совокупности и в то же время закономерность распределения не искажалась случайными колебаниями частот по отдельным разрядам. Существуют нестрогие рекомендации по выбору количества M и размера h таких интервалов, в частности параметр M рекомендуется выбирать с помощью следующих соотношений:

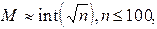
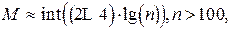
где int(x) - целая часть числа x . Желательно, чтобы n без остатка делилось на M.

Графически статистический ряд отображают в виде гистограммы, полигона и ступенчатой линии. Часто гистограмму представляют как фигуру, состоящую из прямоугольников, основаниями которых служат интервалы длиною h, а высоты равны υ_i/(nh). Такую гистограмму можно интерпретировать как графическое представление эмпирической функции плотности распределения f_n(x), в ней суммарная площадь всех прямоугольников составит единицу. Гистограмма помогает подобрать вид теоретической функции распределения для аппроксимации ЭД.

Полигоном называют ломаную линию, отрезки которой соединяют точки с координатами по оси абсцисс, равными серединам интервалов, а по оси ординат – соответствующим частостям.

Порядок построения гисто­граммы следующий.

1. Построить вариационный ряд, т.е. расположить выборочные значения в порядке возрастания: .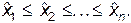

2. Вся область возможных значений 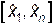разбивается на M непересе­кающихся и примыкающих друг к другу интервалов.

Ai, Bi- соответственно левая и правая границы i-го интервала (Ai+1= Bi);

hi= Bi- Ai- длина i-го интервала;

i- количество чисел в выборке, попадающих в i-тый интервал.

При использовании равноинтервального метода построения гистограммы параметры Ai, Bi, hiвычисляются следующим образом:

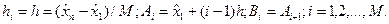
Если при подсчете значений какое-то число в выборке точно совпадает с границей между интервалами, то необходимо в счетчик обоих интервалов прибавить по 0,5.

В случае применения равновероятностного метода границы Ai, Biвыбираются таким образом, чтобы в каждый интервал попадало одинаковое количество выборочных значений:

i= = n / M.

В этом случае

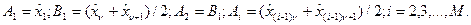
3. Вычисляется средняя плотность вероятности для каждого интервала по формуле

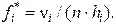
4. На графике провести две оси: x и f*(x) .

5. На оси x отмечаются границы всех интервалов.

6. На каждом интервале строится прямоугольник с основанием hiи высотой 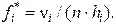Полученная при этом ступенчатая линия называется гистограммой, график которой приблизительно выглядит так, как показано на рис. 2.2.

Замечания.

1. Суммарная площадь всех прямоугольников равна единице.

2. В равновероятностной гистограмме площади всех прямоугольников оди­на­ковы. По виду гистограммы можно судить о законе распределения случай­ной величины.

Достоинства использования гистограммы: простота применения, наглядность.

Пример 2.2. Вариационный ряд случайной величины x имеет вид:
-6,237 -6,229 -5,779 -5,139 -4,950 -4,919 -4,636 -4,560 -4,530 -4,526 -4,523 -4,511 -4,409 -4,336 -4,259 -4,055 -4,044 -4,006 -3,972 -3,944 -3,829 -3,794 -3,716 -3,542 -3,541 -3,431 -3,406 -3,384 -3,307 -3,181 -3,148 -3,124 -3,116 -2,892 -2,785 -2,734 -2,711 -2,637 -2,633 -2,428 -2,381 -2,339 -2,276 -2,222 -2,167 -2,111 -2,034 -1,958 -1,854 -1,803 -1,774 -1,755 -1,745 -1,713 -1,709 -1,566 -1,548 -1,480 -1,448 -1,353 -1,266 -1,229 -1,179 -1,130 -1,102 -1,060 -1,046 -1,035 -0,969 -0,960 -0,903 -0,885 -0,866 -0,865 -0,774 -0,721 -0,688 -0,673 -0,662 -0,626 -0,543 -0,445 -0,241 -0,174 -0,131 0,115 0,205 0,355 0,577 0,591 0,795 0,986 1,068 1,099 1,195 1,540 2,008 2,160 2,534 2,848

Построить гистограмму равноинтервальным и равновероятностным методами.

Решение. Объем выборки равен 100. Количество интервалов определяем так:

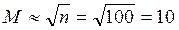
Для равноинтервального метода построения параметры Ai, Bi, i, hi, f^* приведены в табл. 2.1.

Таблица 2.1.

i	Ai	Bi	i	hi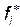
	-6,237	-5,3345		0,9085	0,033
	-5,3345	-4,426		0,9085	0,099
	-4,426	-3,5175		0,9085	0,143
	-3,5175	-2,609		0,9085	0,154
	-2,609	-1,7005		0,9085	0,176
	1,7005	-0,792		0.9085	0,209
	-0,792	0,1165		0,9085	0,132
	0,1165	1,025		0,9085	0,066
	1,025	1,9335		0,9085	0.044
	1,9335	2,848		0,9085	0,044

Ниже приведены интервальная таблица и график гистограммы для равновероятностного метода.

Таблица 2.2

i	Ai	Bi	i	hi
	-6,2370	-4,5245		1,7125	0.0584
	-4,5245	-3,8865		0,6380	0,1567
	-3,8865	-3,1645		0,7220	0,1385
	-3,1645	-2,4045		0,7600	0,1316
	-2,4045	-1,7885		0,6160	0,1623
	-1,7885	-1,3095		0,4790	0,2086
	-1,3085	-0,9319		0,3766	0,2655
	-0,9319	-0,5843		0,3476	0,2877
	-0,5843	0,6932		1,2775	0,0783
	0,6932	2,8480		2,1548	0,0464

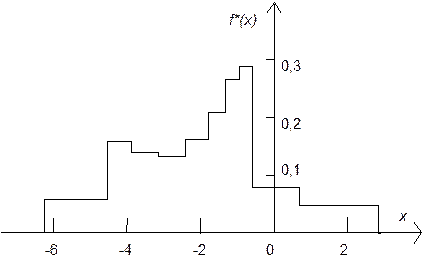
Рис. 2.4

Рассмотренные представления ЭД являются исходными для последующей обработки и вычисления различных параметров.