Первая теорема Чебышева.

Теорема. При достаточно большом числе независимых опытов среднее арифметическое значений случайной величины сходится по вероятности к ее математическому ожиданию:

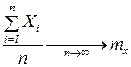
Доказательство: Рассмотрим величину Y равную

.

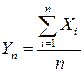Определим числовые характеристики Y_n m_y и D_Y.

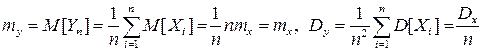
Запишем неравенство Чебышева для величины Y_n

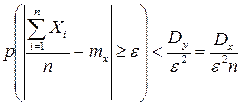
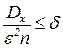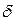Как бы ни было мало число e, можно взять n таким большим, чтобы выполнялось неравенство , где - сколь угодно малое число. Тогда

.

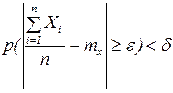Переходя к противоположному событию:

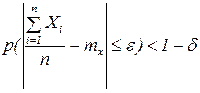
Т.е. вероятность может быть сколь угодно близкой к 1.

1.4.2. Вторая теорема Чебышева:

Теорема. Если Х₁.....Х_n – последовательность попарно независимых СВ с МО m_x1....m_xn и дисперсиями D_x1..D_xn ограничены одним и тем же числом D_xi<L (i=1..n ) , L=const, тогда для любого e, d>0 – бесконечно малых

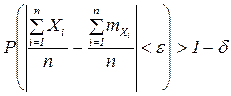или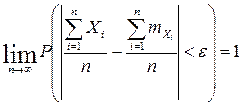

Доказательство: Рассмотрим СВ

.

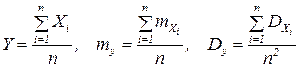Применим к Y неравенство Чебышева:

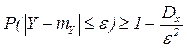или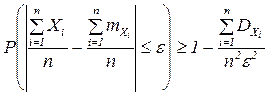

Заменим:

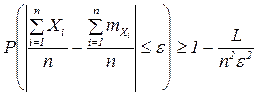
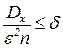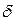Как бы ни было мало число e, можно взять n таким большим, чтобы выполнялось неравенство , где - сколь угодно малое.

Т.е., взяв предел при n®¥ от обеих частей и 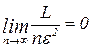получаем:

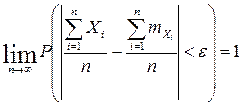
(так как вероятность не может быть больше 1).

Пример1.1. Производится большое число n независимых опытов, в каждом из которых некоторая случайная величина имеет равномерное распределение на участке [1,2]. Рассматривается среднее арифметическое наблюденных значений случайной величины X. На основании Закона больших чисел выяснить, к какому числу а будет приближаться величина Y при n→∞. Оценить максимальную практически возможную ошибку равенства Y≈a.

Решение. .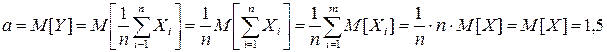

.

.

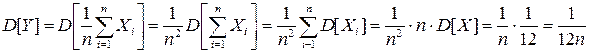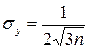Максимальное практически возможное значение ошибки .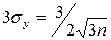

ТЕОРЕМА БЕРНУЛЛИ

Пусть произведены n независимых опытов, в каждом из которых возможно событие А с вероятностью р. Тогда относительная частота появления события А в n опытах стремится по вероятности к вероятности появления А в одном опыте.

Теорема Бернулли: При неограниченном увеличении числа опытов до n частота события А сходится по вероятности к его вероятности р: ,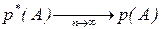

где 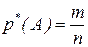-- частота события А в n опытах, где m-число опытов в которых произошло событие А, n-число проведенных опытов 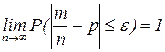или

или .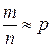

Событие Х_i – число появлений события А в i-м опыте. СВ X может принимать только два значения: X=1 (событие наступило) и X=0 (событие не наступило). Пусть СВ Х_i – индикатор события А в i-м опыте . Числовые характеристики х_i: m_i = p D_i = pq.

Они независимы, следовательно, можем применить теорему Чебышева:

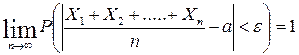
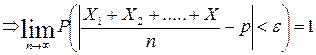
Дробь 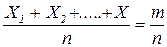равна относительной частоте появлений события А в испытаниях Þ получаем

.

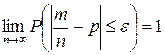Пояснения: В теореме речь идет лишь о вероятности того, что при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании.

Теорема Бернулли объясняет, почему относительная частота при достаточно большом числе испытаний обладает свойством устойчивости и оправдывает статистическое определение вероятности: в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней.