Методика расчета электропривода на технический оптимум

При проектировании и расчете систем управления электроприводами обычно выбор закона регулирования и расчет параметров настройки регуляторов производится по простейшей методике, получившей условное название расчет на «технический оптимум» [7, 8, 12]. Математического определения критерия оптимальности «технический оптимум» не имеет. Фактически расчет каждого из контуров управления производится по предельно упрощенной модели, совпадающей с реальным объектом в диапазоне частот от частоты среза до тройной частоты среза. Не смотря на такие упрощения моделей методика дает вполне приемлемые результаты и широко применяется в практике расчетов регуляторов электроприводов.

Методику расчета на «технический оптимум» можно интерпретировать как последовательный расчет контуров с дихотомным делением частот среза. Базовой является частота среза 1/T силового преобразователя. Частоту среза токового контура уменьшают в 2 раза, также как и каждого последующего контура. При этом контур скорости с ПИ-регулятором рассматривают как два контура: для пропорциональной и для интегральной составляющей закона регулирования.

Технически оптимальным переходным процессом считается процесс, обеспечивающий минимальное время достижения согласованного положения 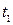при перерегулировании 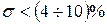(процесс 2 на рис. 6.2).

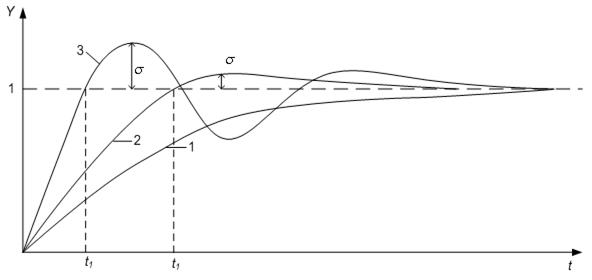
Рис. 6.2

Такой процесс является компромиссным между процессом более быстрым, но с большим перерегулированием (процесс 3) и процессом без перерегулирования, но более медленным (процесс 1). Для получения переходных процессов, изображенных на рис. 6.2, передаточная функция разомкнутого контура должна иметь вид

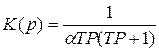, (6.1)

а замкнутый контур будет описываться передаточной функцией колебательного звена

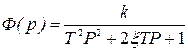. (6.2)

В зависимости от величины 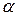(коэффициента затухания 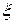) можно получить процессы вида 1, 2 и 3.

Структурная схема контура изображена на рис. 6.3.

На рисунке 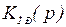– передаточная функция объекта с регулятором.

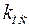– коэффициент передачи датчика обратной связи (тока, скорости, положения).

Передаточная функция разомкнутого контура

,

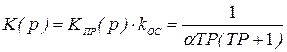а передаточная функция замкнутого контура

,

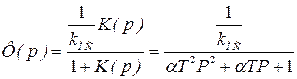соответствует колебательному звену с постоянной времени , .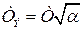

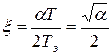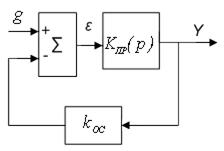
Рис. 6.3

При 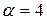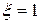получим процесс вида 1.

При 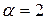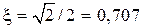– процесс вида 2 с временем первого согласования .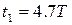

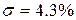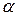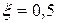При =1 – процесс колебательный типа 3.

Для получения технически оптимального переходного процесса характеристическое уравнение замкнутого контура должно иметь вид

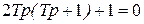, (6.3)

т.е. соответствовать колебательному звену с коэффициентом затухания ξ = 0,707.

Если рассчитываемый контур описывается уравнением выше второго порядка, то для получения технически оптимального переходного процесса, его коэффициенты должны иметь следующие соотношения:

,

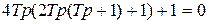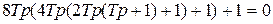. (6.4)

При таком соотношении коэффициентов характер переходного процесса, как указывается в [7, 8], будет определяется вырожденным уравнением второго порядка, соответствующим колебательному звену с коэффициентом затухания ξ=0,707, приведенным в табл. 6.1.

Таблица 6.1

Порядок уравне–ния	Характеристическое уравнение	Вырожденное уравнение
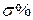
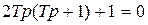
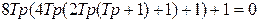
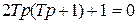
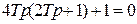
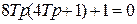
			4,7Т 7,6Т 14,4Т	4,3 6,2

При расчете электропривода на «технический оптимум» расчет начинают с внутреннего (токового) контура. Закон регулирования и параметры настройки регуляторов выбирают такими, чтобы замкнутый контур сводился к эквиваленту колебательного звена с коэффициентом затухания ξ = 0,707.

6.2.1. Расчет токового контура на технический оптимум. Структурная схема привода с регуляторами тока, скорости и положения изображена на рис. 6.4.

На структурной схеме двигатель представлен структурной схемой с обратной связью по ЭДС. 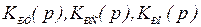– передаточные функции регуляторов, законы регулирования которых и параметры их настройки необходимо

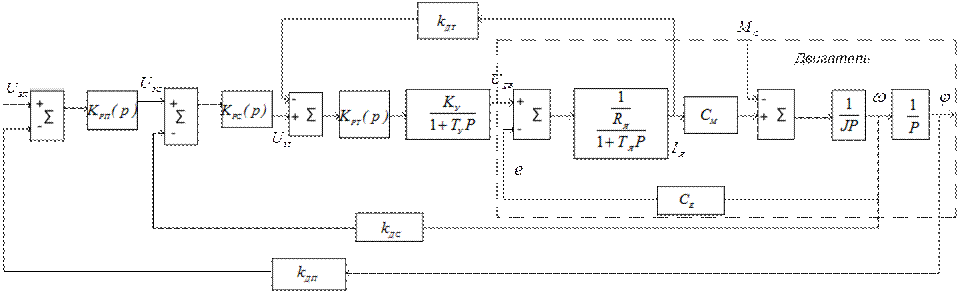
Рис. 6.4. Структурная схема электропривода

определить. 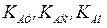– коэффициенты передачи датчиков тока, скорости и положения.

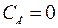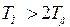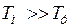Расчет начинается с внутреннего токового контура. Для упрощения расчета, чтобы избавиться от перекрестной обратной связи, полагают, что , т.е. пренебрегают обратной связью по ЭДС двигателя. Такое предположение допустимо, если за время переходного процесса в таковом контуре скорость вращения двигателя изменится несущественно. В [7] указывается, что это допустимо, если и , где 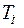– электромеханическая постоянная времени двигателя.

Расчетная структурная схема токового контура при этом примет вид изображенный на рис. 6.5.

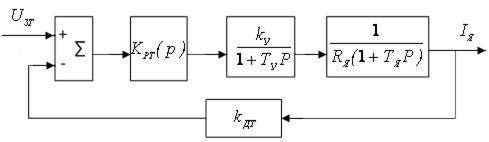
Рис. 6.5

Передаточная функция разомкнутого токового контура

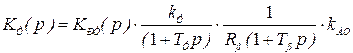. (6.5)

Для получения передаточной функции, обеспечивающей технически оптимальный переходной процесс, желаемая передаточная функция разомкнутого контура должна иметь вид

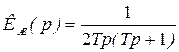. (6.6)

Для получения такой передаточной функции в таковой контур необходимо ввести интегратор и компенсировать одну инерционность, что можно осуществить ПИ–регулятором

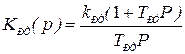. (6.7)

Параметры настройки регулятора 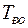и 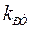выбираются из условия компенсации большей постоянной времени 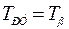, так как время переходного

процесса будет определяться некомпенсированной (меньшей) постоянной

времени. Коэффициент передачи регулятора тока 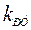рассчитывается из условия равенства коэффициента передачи контура желаемому

,

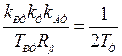откуда 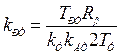. (6.8)

При таких параметрах настройки передаточная функция замкнутого токового контура будет эквивалентна колебательному звену коэффициентом затухания ξ= 0,707.

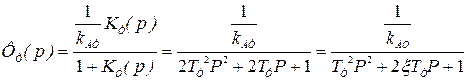, (6.9)

где , .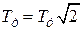

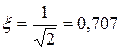В дальнейших расчетах при расчете скоростного контура, чтобы свести его к эквиваленту колебательного звена, передаточную функцию замкнутого токового контура аппроксимируют инерционным звеном первого порядка, т.е. пренебрегают старшей степенью 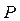в выражении (6.9)

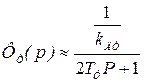. (6.10)

6.2.2. Расчет скоростного контура на технический оптимум. Структурная схема скоростного контура приведена на рис. 6.6.

Передаточная функция разомкнутого скоростного контура

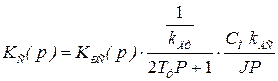. (6.11)

Так как в 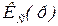имеется интегратор и инерционное звено, то для получения желаемой передаточной функции (6.6) можно использовать П–регуля-тор .

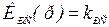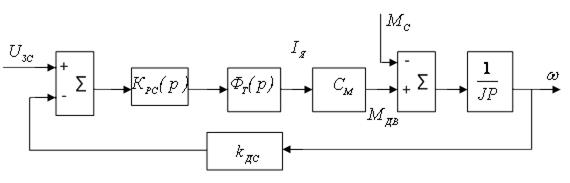
Рис. 6.6

Коэффициент передачи регулятора определим, приравнивая 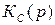к желаемой

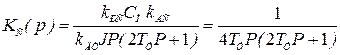, (6.12)

откуда

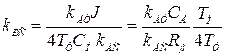. (6.13)

Передаточная функция замкнутого скоростного контура

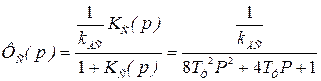. (6.14)

эквивалентна колебательному звену с постоянной времени 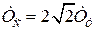и коэффициентом затухания ξ=0,707.

В дальнейших расчетах при расчете позиционного контура, скоростной контур описывают передаточной функцией инерционного звена превого порядка

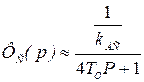, (6.15)

пренебрегая слагаемым 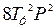в (6.14).

Следует отметить, что требуемый коэффициент передачи регулятора скорости зависит от момента инерции нагрузки и, в случае изменения последнего в процессе работы привода, для сохранения настройки на технический оптимум требуется подстройка коэффициент передачи регулятора.

Скоростной контур с П–регулятором скорости, обладая астатизмом первого порядка по задающему сигналу 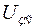, является статическим по возмущению 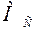. Это значит, что в установившемся режиме работы скорость привода будет отличаться от заданной. Установившаяся скорость привода может быть определена исходя из условия, что в установившемся режиме сигнал задания на входе ПИ–регулятора тока должен быть равен нулю.

.

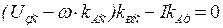откуда

.

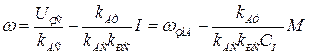Подставив в это выражение 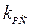из (6.13) получим

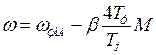. (6.16)

Из (6.16) видно, что точность поддержания скорости в замкнутом приводе будет выше, чем в разомкнутом, если .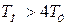

Для повышения точности скоростного контура применяют ПИ–регулятор скорости, который обеспечивает астатизм по возмущению. Параметры его настройки рассчитывают на «симметричный оптимум», обеспечивающий симметрию ЛАХ скоростного контура относительно частоты среза.

Передаточная функция ПИ–регулятора скорости

.

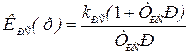Коэффициент передачи регулятора выбирают как и у П–регулятора по выражению (6.13), а постоянную времени изодрома берут равной .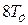

ЛАХ скоростного контура, настроенного на симметричный оптимум, изображена на рис. 6.7.

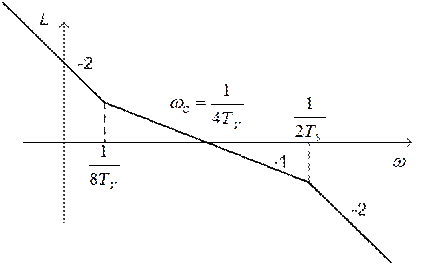
Рис. 6.7

Передаточная функция разомкнутого скоростного контура

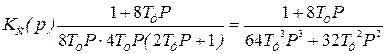. (6.17)

Передаточная функция замкнутого контура

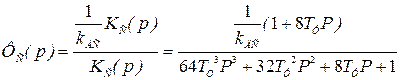. (6.18)

Наличие форсирующего звена 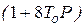в числителе (6.18) и малая протяженность среднечастотной части ЛАХ (рис. 6.7), составляющая 0,6 декады, приводят к колебательности этого контура. Величина перерегулирования на ступенчатое задание скорости превышает 45%. Для уменьшения перерегулирования при настройке на симметричный оптимум рекомендуется устанавливать задатчик интенсивности с передаточной функцией

,

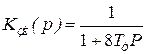в цепи задания скоростного контура.

Структурная схема скоростного контура с задатчиком интенсивности изображена на рис. 6.8.

Задатчик интенсивности компенсирует форсировку в скоростном контуре. При этом 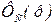примет вид

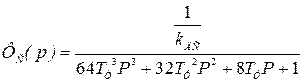. (6.19)

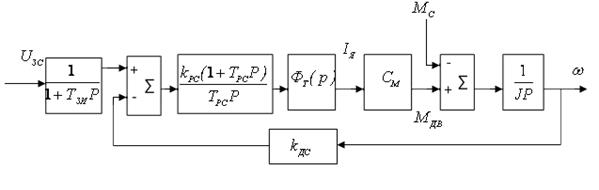
Рис. 6.8

Если пренебречь старшим слагаемым 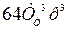, то получим колебательное звено с постоянной времени 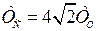и коэффициентом затухания ξ = 0,707.

Для уменьшения перерегулирования в скоростном контуре, настроенном на симметричный оптимум в [15] предлагается вместо задатчика интенсивности использовать обратную связь по ускорению с передаточной функцией

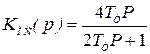, (6.20)

включенную параллельно цепи сигнала датчика скорости.

Структурная схема скоростного контура с обратной связью по ускорению изображена на рис. 6.9.

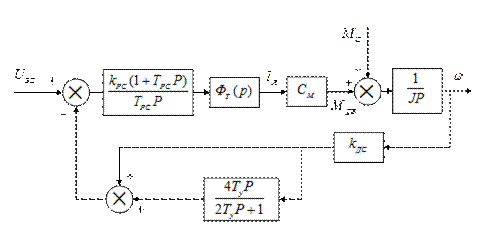
Рис. 6.9

В дальнейших расчетах при расчете позиционного контура замкнутый скоростной контур описывают передаточной функцией инерционного звена первого порядка, пренебрегая двумя старшими слагаемыми в знаменателе выражения (6.19).