Расчет позиционного контура на технический оптимум. Расчет контура ведется аналогично расчету внутренних (токового и скоростного) контуров.
Структурная схема позиционного контура представлена на рис. 6.10.
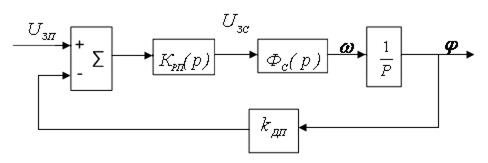
Рис. 6.10
Для того чтобы свести позиционный контур к эквиваленту колебательного звена замкнутый скоростной контур описывают передаточной функцией инерционного звена первого порядка.
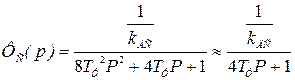 . (6.21)
. (6.21)
при использовании П–регулятора скорости, настроенном на технический оптимум, или
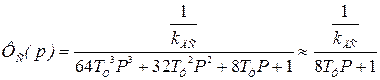 , (6.22)
, (6.22)
при ПИ–регуляторе скорости с задатчиком интенсивности, настроенном на симметричный оптимум.
При такой аппроксимации скоростного контура для получения желаемой передаточной функции вида (6.6) в позиционном контуре можно использовать П–регулятор 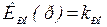 .
.
Передаточная функция разомкнутого позиционного контура
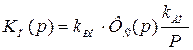 . (6.23)
. (6.23)
Подставив сюда 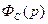 из (6.21) или (6.22) получим
из (6.21) или (6.22) получим
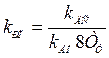 ,
,
при П–регуляторе скорости, и
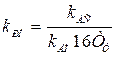 , (6.24)
, (6.24)
при ПИ–регуляторе скорости с задатчиком интенсивности.
Методика расчета на технический оптимум достаточно проста и наглядна, однако ей присущи существенные недостатки.
1. В расчетах используется упрощенная математическая модель двигателя (пренебрегается внутренней обратной связью по скорости – 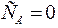 ), при этом якорная цепь двигателя описывается передаточной функцией инерционного звена
), при этом якорная цепь двигателя описывается передаточной функцией инерционного звена
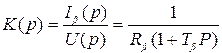 . (6.25)
. (6.25)
2. Законы регулирования и параметры настройки регуляторов выбираются такими, чтобы замкнутый контур был эквивалентен колебательному звену с коэффициентом затухания ξ = 0,707, а при расчете следующего, внешнего контура, это колебательное звено приближённо заменяется инерционным звеном первого порядка (понижается порядок характеристического уравнения отбрасыванием старшего слагаемого).
3. В процессе расчетов добиваются локальных технических оптимумов для упрощенной модели каждого контура в отдельности, которые не обеспечивают глобального оптимума для привода в целом.
6.3. Расчет электропривода методом типовых нормированных
уравнений
6.3.1. Нормированные уравнения и их свойства. Этот метод базируется на способе нормирования характеристических уравнений, предложенном Вышнеградским, для систем третьего порядка.
Нормирование уравнения приводит к новому уравнению того же порядка, у которого коэффициент при старшей степени и свободный член равны
единице.
Пусть имеется характеристическое уравнение замкнутой системы
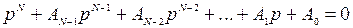 . (6.26)
. (6.26)
Его можно переписать в виде
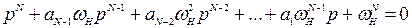 (6.29)
(6.29)
где: 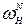 =A – частота нормировки, определяющая длительность переходных характеристик с сохранением их формы. Форма переходных характеристик определяется набором коэффициентов
=A – частота нормировки, определяющая длительность переходных характеристик с сохранением их формы. Форма переходных характеристик определяется набором коэффициентов 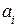 нормированного уравнения.
нормированного уравнения.
6.3.2. Типовые нормированные уравнения. В литературе по автоматическому регулированию и управлению разные авторы предлагают различный вид нормированных уравнений, обеспечивающих качество регулирования, близкое оптимальному.
Так, Д. Грехем и Р. Летроп [17] в качестве оптимальных, предлагают уравнения, дающие минимум интегральной оценки
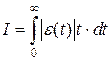 . (6.32)
. (6.32)
С. Баттерворт в качестве оптимального предлагает нормированное уравнение, корни которого равномерно расположены на полуокружности единичного радиуса. При этом обеспечивается монотонность АЧХ замкнутой системы. В отечественной литературе по электроприводам рекомендуются уравнения, обеспечивающие технический оптимум, рассмотренные ранее.
Наиболее полные таблицы нормированных уравнений от второго до восьмого порядка включительно с указанием качественных показателей переходного процесса приведены в [17].
Из этого множества типовых нормированных уравнений для расчета систем управления электроприводами целесообразно использовать уравнения от второго до шестого порядка, обеспечивающие процессы без перерегулирования или с 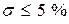 и минимальное нормированное время переходного процесса [16], приведенные в табл. 6.2.
и минимальное нормированное время переходного процесса [16], приведенные в табл. 6.2.
Таблица 6.2
| № пп | Нормированные уравнения | 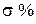
| 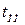
| 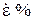
|
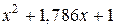
| 4,0 | |||
| 2* | 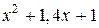
| 4,5 | 2,8 | |
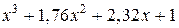
| 4,0 | |||
| 4* | 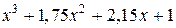
| 3,0 | 3,6 | |
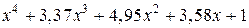
| 5,6 | |||
| 6* | 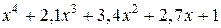
| 10,2 | 4,7 | |
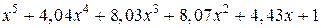
| 5,9 | |||
| 8* | 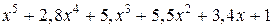
| 6,0 | 5,2 | |
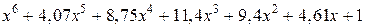
| 7,4 | |||
| 10* | 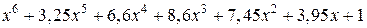
| 5,4 | ||
*– уравнения, обеспечивающие минимум интегральной оценки 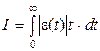 . .
|
Действительное значение максимальной скорости отработки определяется выражением 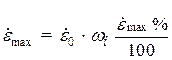 .
.
Располагая таблицами нормированных уравнений и соответствующих им качественных показателей переходного процесса, расчет систем может быть произведен в такой последовательности:
1. Составляется структурная схема исходной системы и определяется ее характеристическое уравнение.
2. По таблицам выбирается типовое нормированное уравнение того же порядка, удовлетворяющее требуемым качественным показателям.
3. Определяется коэффициент нормирования по одному из выражений
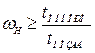 . (6.33)
. (6.33)
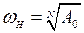 , (6.35)
, (6.35)
где 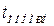 – нормированное время переходного процесса (из таблиц);
– нормированное время переходного процесса (из таблиц);
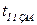 – заданное время переходного процесса (из Т.З.);
– заданное время переходного процесса (из Т.З.);
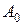 – свободный член исходного ненормированного уравнения.
– свободный член исходного ненормированного уравнения.
Выражение (6.33) обеспечивает получение заданного времени переходного процесса. При вычислении коэффициента нормирования по выражению (6.35) не потребуется изменять свободный член характеристического уравнения, который обычно определяется коэффициентом усиления разомкнутой системы, и может вычисляться из условия обеспечения заданной точности.
6.3.3. Расчет моментого электронривода, состоящего только из токового контура. Структурная схема привода приведена на рисунке 6.4. Требуется определить закон регулирования регулятора тока 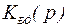 и рассчитать параметры его настройки, обеспечивающие заданное качество регулирования тока
и рассчитать параметры его настройки, обеспечивающие заданное качество регулирования тока 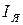 . Объектом регулирования в данном случае является якорная цепь двигателя. С учетом обратной связи по ЭДС передаточная функция объекта определяется выражением
. Объектом регулирования в данном случае является якорная цепь двигателя. С учетом обратной связи по ЭДС передаточная функция объекта определяется выражением
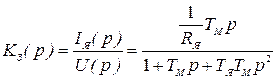 , (6.37)
, (6.37)
где 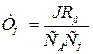 – электромеханическая постоянная времени двигателя.
– электромеханическая постоянная времени двигателя.
В зависимости от соотношения постоянных времени 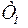 и
и 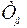 , знаменатель может быть представлен в виде
, знаменатель может быть представлен в виде
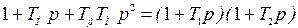 при
при 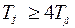 , (6.38)
, (6.38)
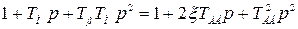 при
при 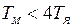 , (6.39)
, (6.39)
где 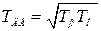
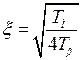 .
.
Так как объект является дифференциатором, то для регулирования тока необходимо использовать ПИ–регулятор
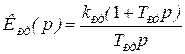 .
.
Структурная схема токового контура с ПИ–регулятором тока изображена на рис. 6.11.
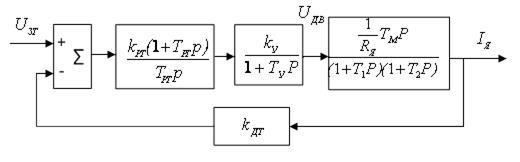
Рис. 6.11
Постоянная времени изодрома регулятора тока 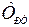 выбирается равной меньшей постоянной времени объекта
выбирается равной меньшей постоянной времени объекта 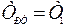 , если объект описывается характеристическим уравнением (6.38) или
, если объект описывается характеристическим уравнением (6.38) или 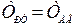 при характеристическом уравнении (6.39).
при характеристическом уравнении (6.39).
Передаточная функция разомкнутого токового контура
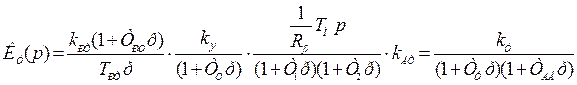 , (6.40)
, (6.40)
где 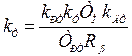 – коэффициент передачи токового контура;
– коэффициент передачи токового контура;
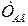 – некомпенсированная постоянная времени двигателя;
– некомпенсированная постоянная времени двигателя;
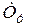 – постоянная времени усилителя мощности.
– постоянная времени усилителя мощности.
Передаточная функция замкнутого токового контура
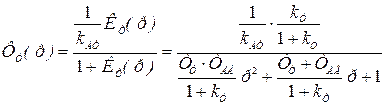 . (6.41)
. (6.41)
Токовый контур представляет собой колебательное звено с коэффициентом передачи 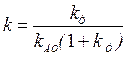 , постоянной времени
, постоянной времени 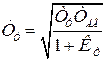 и коэффициентом затухания
и коэффициентом затухания 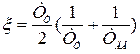 .
.
Характеристическое уравнение замкнутого токового контура можно записать в виде
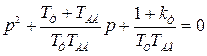 . (6.42)
. (6.42)
где kт - коэффициент усиления разомкнутого контура тока.
Для получения заданного качества регулирования в токовом контуре необходимо выбрать типовое нормированное уравнение второго порядка
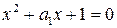 . (6.43)
. (6.43)
Желаемое характеристическое уравнение
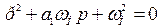 . (6.44)
. (6.44)
Приравняв коэффициенты исходного уравнения (6.42) и желаемого (6.44) однозначно определим коэффициент нормирования и коэффициент передачи токового контура
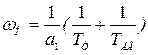
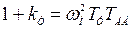 , (6.45)
, (6.45)
откуда определяются параметры настройки регулятора тока
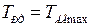 ;
;
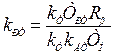 . (6.46)
. (6.46)
При таких параметрах настройки качество регулирования в токовом контуре будет определяться выбранным типовым нормированным уравнением второго порядка (6.43).
6.3.4. Расчет скоростного электропривода. К моментному электроприводу добавляется контур регулирования скорости. С П-регулятором скорости электропривод будет астатическим по задающему сигналу, однако он будет статическим по возмущению 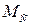 . Для астатизма по возмущению обычно использоваться ПИ–регулятор скорости.
. Для астатизма по возмущению обычно использоваться ПИ–регулятор скорости.
При установке пропорционального регулятора передаточная функция замкнутого скоростного электропривода примет вид
. 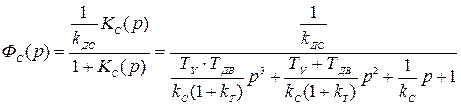 (6.49)
(6.49)
Характеристическое уравнение скоростного электропривода можно записать в виде
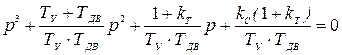 . (6.50)
. (6.50)
где kс - коэффициент усиления разомкнутого контура скорости.
Для получения заданного качества регулирования необходимо выбрать характеристическое уравнение третьего порядка
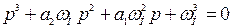 . (6.52)
. (6.52)
Приравняв коэффициенты исходного и желаемого уравнений, получим выражение для расчета коэффициента нормирования и коэффициентов передачи регуляторов тока и скорости
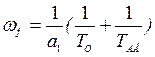 ;
; 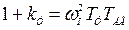 ;
; 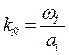 . (6.53)
. (6.53)
Астатизм по возмущению 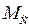 будет обеспечиваться при установке ПИ–регулятора скорости
будет обеспечиваться при установке ПИ–регулятора скорости 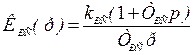 . При этом передаточная функция замкнутого скоростного электропривода будет
. При этом передаточная функция замкнутого скоростного электропривода будет
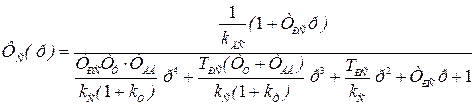 , (6.55)
, (6.55)
Характеристическое уравнение может быть записано в виде
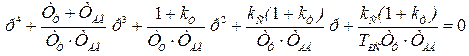 . (6.56)
. (6.56)
Для получения заданного качества регулирования необходимо выбрать желаемое характеристическое уравнение четвертого порядка
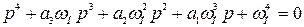 . (6.57)
. (6.57)
Приравняв коэффициенты исходного (6.56) и желаемого (6.57) уравнений получим выражения для расчета коэффициента нормирования и параметров настройки регуляторов тока и скорости
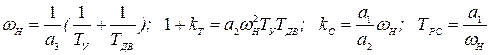 . (6.58)
. (6.58)
Следует отметить, что для компенсации нуля ПИ-регулятора скорости и уменьшения перерегулирования рекомендуется в цепи задания скорости устанавливать задатчик интенсивности, представляющий собой инерционное звено с постоянной времени, равной постоянной времени форсировки.
При этом передаточная функция замкнутого скоростного электропривода будет полностью соответствовать выбранному типовому нормированному уравнению.
6.3.5. Расчет позиционного электропривода. Дополняем скоростногй электропривод интегратором, преобразующий частоту вращения двигателя 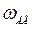 в угол поворота
в угол поворота 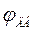 , датчиком положения и П-регулятором, т.е. организуем позиционномый контур управления. При использовании ПИ–регулятора скорости задатчик интенсивности войдет в П-регулятор положения.
, датчиком положения и П-регулятором, т.е. организуем позиционномый контур управления. При использовании ПИ–регулятора скорости задатчик интенсивности войдет в П-регулятор положения.
Передаточная функция замкнутого позиционного электропривода
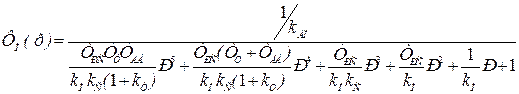 , (6.61)
, (6.61)
где 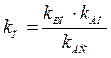 .
.
Характеристическое уравнение можно записать в виде
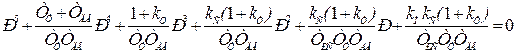 . (6.62)
. (6.62)
где kп - коэффициент усиления разомкнутого контура положения.
Желаемое характеристическое уравнение также должно быть пятого порядка
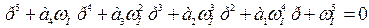 . (6.63)
. (6.63)
Приравняв коэффициенты уравнений (6.62) и (6.63) получим расчетные соотношения для определения параметров настройки регуляторов.
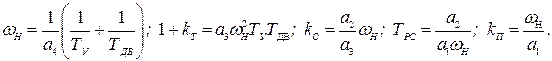 (6.64)
(6.64)
Для удобства практического использования основные соотношения для расчета параметров настройки регуляторов методом типовых нормированных уравнений сведены в табл. 6.3.
Таблица 6.3

| № п/п | Передаточные функции регуляторов | Порядок характ. уравнения | Параметры настройки электроприводов | ||
| Положения | Скорости | Тока | |||
| 1. | 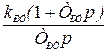
| 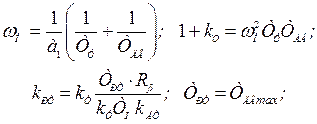
| |||
| 2. | 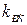
| 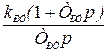
| 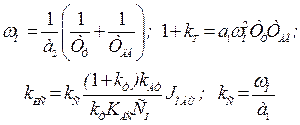
|
| 3. | 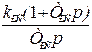
| 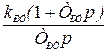
| 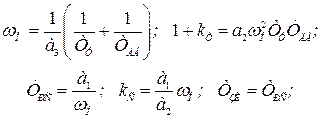
| ||
| 4. | 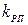
| 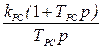
| 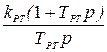
| 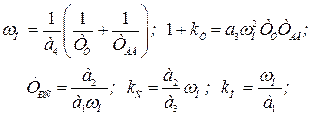
| |
| 5. | 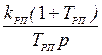
| 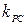
| 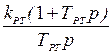
| 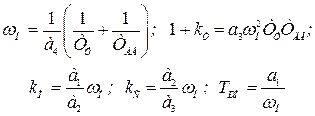
|

Изложенная выше задача расчета всех регуляторов электропривода как единого модального регулятора решена [16] на основе метода стандартных коэффициентов. Использование метода стандартных коэффициентов позволило параллельно рассчитывать все регуляторы с учетом взаимовлияния всех контуров управления и без традиционных упрощений модели электродвигателя.
Предлагается еще более простой метод расчета регуляторов многоконтурного электропривода, задающий частоты среза всех контуров управления. Была создана система автоматизированного проектирования регуляторов в среде Matlab, результаты работы которой здесь анализируются.
6.3.6. Типы и свойства эталонных моделей электроприводов. При наилучшей настройке регуляторы всех контуров образуют единый модальный регулятор, настроенный на один из критериев оптимальности по выбору. Критерий задается эталонной моделью замкнутой системы в виде передаточной функции с единицей в числителе и нормированным (с равным единице свободным членом) полиномом в знаменателе. Используются известные критерии:
1. «минимум интеграла модуля ошибки, умноженной на время» 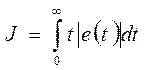 (полиномы Латропа –Грехема);
(полиномы Латропа –Грехема);
2. фильтр Баттерворда;
3. «кратные действительные полюсы»;
4. «технический и симметричный оптимумы»;
5. «минимум интеграла квадрата ошибки»;
6. «апериодические процессы» – эмпирический набор моделей с комплексными полюсами, более быстрыми, чем с действительными полюсами [17].
Все вышеперчисленные модели, кроме «минимума интеграла квадрата ошибки», имеют показатель колебательности АЧХ равный единице.
Методика точного расчета всех регуляторов многоконтурного сервопривода как единого модального регулятора не сложнее традиционно используемой методики на «технический оптимум» и сводится к выполнению определенных соотношений между частотами среза всех контуров управления, включая частоту среза силового преобразователя.
Соотношения частот среза контуров легко вычисляются как вторые отношения коэффициентов полинома выбранной эталонной модели.
В сервоприводах допускающих перерегулирование следует использовать эталонную модель с полиномом Латропа-Грехема как наиболее быструю с малым (2 %) перерегулированием.
В сервоприводах не допускающих перерегулирование следует использовать эталонную модель с апериодическими процессами.
Переходные характеристики эталонных моделей для электроприводов с регуляторами ПИ тока, П скорости, П положения приведены на рис. 6.12

Рис. 6.12
Основные характеристики различных эталонных моделей многоконтурного сервопривода приведены в табл. 6.4.
Как видно из таблицы, применение для сервопривода с дискретным силовым преобразователем эталонной модели с минимумом интегральной квадратичной ошибки недопустимо из за гарантированной потери устойчивости контура тока, вследствии выхода частоты среза за граничную частоту силового преобразователя.
Таблица 6.4
Характеристики эталонных моделей многоконтурного сервопривода
| ПИ регулятор тока П регулятор скорости П регулятор положения | Латроп Грехем | Апериодические процессы | Кратные полюсы | Баттерворд | Техн. оптимум | Квадратичный минимум | |
| Диапазон частот среза контуров, wc_усил.мощн./wc_положения | 5,67 | 11,7 | 6,76 | ||||
| Разнос частот среза контуров | wc_усил.мощн./wc_тока | 1,3 | 2,33 | 2,67 | 0,33 | ||
| wc_тока/wc_скорости | 2,04 | 2,02 | 2,25 | 1,71 | 4,5 | ||
| wc_скорости/wc_поло-жения | 2,14 | 2,49 | 2,67 | 1,33 | |||
| Запасы по фазе контуров | тока | ||||||
| скорости | |||||||
| положения | |||||||
| ПИ регулятор тока ПИ регулятор скорости П регулятор положения | |||||||
| Диапазон частот среза контуров, wc_усил.мощн./wc_положения | 9,52 | 17,9 | 10,5 | ||||
| Разнос частот среза контуров | wc_усил.мощн./wc_тока | 1,57 | 2,03 | 2,5 | 0,25 | ||
| wc_тока/wc_скорости | 1,62 | 1,98 | 1,62 | 5,33 | |||
| wc_скорости/wc_интег.скор | 1,78 | 1,83 | 1,62 | 0,75 | |||
| wc_интег.скор./wc_по-ложен. | 2,1 | 2,43 | 2,5 | ||||
| Запасы по фазе контуров | тока | ||||||
| скорости | |||||||
| положения |
ЛИТЕРАТУРА
ОСНОВНАЯ
1. Солодовников, В. В. Основы теории и элементы систем автоматического регулирования / В. В. Солодовников, В. Н. Плотников, А. М. Яковлев. – M. : Машиностроение, 1985.
2. Основы проектирования следящих систем / под ред. Н. А. Лакоты. – М. : Машиностроение, 1978.
3. Мирошник, И. В. Теория автоматического управления : учеб. пособие. В 2 ч. / И. В. Мирошник. – СПб. : Питер, 2005 ; 2006.
4. Горбачев, А. Д. и др. Проектирование и надежность систем автоматики и телемеханики. – Минск: Высш. шк., 1981.
5. Руководство по проектированию систем автоматического управления / под ред. В. А. Бесекерского. – М. : Высш. шк., 1984.
6. Герман-Галкин, С. Г. Matlab & Simulink: Проектирование мехатронных систем на ПК / С. Г. Герман-Галкин. – М. : Корона-Век, 2008.
7. Терехов, В. М. Системы управления электроприводов / В. М. Терехов, О. И. Осипов. – М. : Академия, 2005.
8. Белов, М. П. Автоматизированный электропривод типовых производственных механизмов и технологических комплексов : учебник для вузов / М. П. Белов, В. А. Новиков, Л. Н. Рассудов. – М. : Академия, 2004.
9. Наладка средств автоматизации и автоматических систем регулирования. / Под ред. А. С. Клюева. – М.: Энергоатомиздат, 1989.
10. Козярук, А. Е. Современное и перспективное алгоритмическое обеспечение частотно-регулируемых электроприводов / А. Е. Козярук, В. В. Рудаков, А. Г. Народицкий. – СПб. : СПЭК, 2004.
ДОПОЛНИТЕЛЬНАЯ
11.Михайлов, О. П. Автоматизированный электропривод станков и промышленных роботов / О. П. Михайлов. – М. : Машиностроение, 1990.
12.Водовозов, В. М. Теория и системы электропривода : учеб. пособие / В. М. Водовозов. – СПб. : СПбГЭТУ «ЛЭТИ», 2004.
13.Водовозов, В. М. Курсовое проектирование электропривода : учеб. пособие / В. М. Водовозов. – СПб. : СПбГЭТУ «ЛЭТИ», 2004.
14. Герасимяк, Р. П. Анализ и синтез крановых электромеханических систем / Р. П. Герасимяк, В. П. Лещев. – Одесса : СМИЛ, 2008.
15.Системы программного управления промышленными установками и робототехническими комплексами / Б. Г. Коровин [и др.]. – Л. : Энергоатомиздат, 1990.
16. Красовский, А. Я., Хаджинов, М. К. Расчет многоконтурных систем управления электроприводами. – Минск: БГУИР, 1996.
17. Яворский, В. Л. и др. Проектирование инвариантных следящих приводов. – М.: Высш. шк., 1963.
18. Ротач, В. Я. Расчет динамики промышленных автоматических систем регулирования. – М.: Энергия 1983.
19.Коробейников А.Г., Разработка и анализ математических моделей с использованием MATLAB и MAPLE. ИТМО, СПб, 2010. – 144 с.
20.Хаджинов, М. К. Методическое пособие к лабораторным работам по курсу «Автоматизированное проектирование систем управления на ПЭВМ» / М. К. Хаджинов, А. С. Леошин. – Минск : БГУИР, 1998.
21.Антипова, М. А. методическое пособие к лабораторным работам по курсу «Автоматизированный расчет систем управления» / М. А. Антипова, М. К. Хаджинов. – Минск : БГУИР, 2004.
Дата добавления: 2022-02-05; просмотров: 762;











