Типовые законы регулирования и их характеристики

Если в промышленной системе регулирования датчик обратной связи отнести к объекту регулирования, т. е. считать выходным сигналом системы нормированный сигнал датчика, пропорциональный величине регулируемой переменной, то структурная схема промышленной САР примет вид рис. 5.3.

Передаточная функция разомкнутой системы:

;

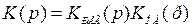Передаточная функция замкнутой системы:

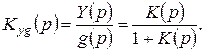
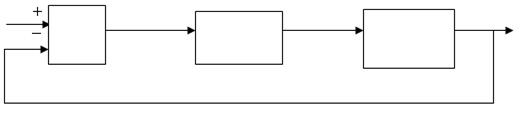
Рис. 5.3

Система будет идеальной, то есть будет отрабатывать задающее воздействие g без ошибки, если .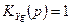

Однако достичь этого при значительной инерционности объекта и наличии чистого запаздывания невозможно. Если систему с запаздыванием оптимизировать по минимуму квадрата ошибки [4], то в качестве приближения к идеалу можно принять

,

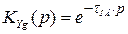т.е. система воспроизводит на выходе задающее воздействие g(t), но с запаздыванием на время 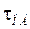(см. рис. 5.4).

Рис. 5.4

При такой передаточной функции К_уg(р), передаточная функция разомкнутой системы:

, (5.2)

а желаемая передаточная функция регулятора

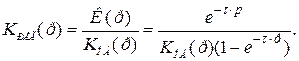(5.3)

Учитывая, что в полосе пропускания системы 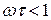, можно функцию 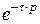разложить в ряд Маклорена и ограничиться в разложении линейными членами

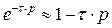. (5.4)

Подставив (5.4) в знаменатель (5.3) получим

. (5.5)

Подставляя в (5.5) выражения различных передаточных функций объекта регулирования 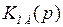получим передаточные функции типовых регуляторов.

Так для астатического объекта с чистым запаздыванием, описываемого передаточной функцией

(5.6)

получим пропорциональный регулятор с передаточной функцией

(5.7)

Такой регулятор имеет один параметр настройки

Для безинерционного объекта с чистым запаздыванием при

(5.8)

получим интегральный регулятор

(5.9)

где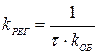

Этот регулятор также имеет один параметр настройки .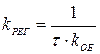

Для инерционного объекта с чистым запаздыванием

, (5.10)

близким к оптимальному будет пропорционально-интегральный закон регулирования

, (5.11)

где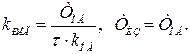

У такого регулятора два параметра настройки – коэффициент передачи

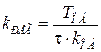и постоянная времени изодрома 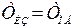– время, когда интегральная составляющая выходного сигнала регулятора станет равной пропорциональной.

Для объектов, описываемых передаточной функцией

, (5.12)

получим пропорционально-дифференциальный (ПД)– регулятор

, (5.13)

с двумя параметрами настройк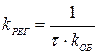и

и .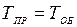

Если объект описывается передаточной функцией колебательного звена с запаздыванием

, (5.14)

то для него близким к идеальному будет пропорционально–интегрально–дифференциальный (ПИД) – регулятор с передаточной функцией

(5.15)

У этого регулятора три параметра настройки. Коэффициент передачи регулятора 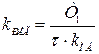, постоянная времени изодрома 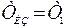и постоянная времени предварения .

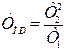Передаточные функции, логарифмические, частотные и переходные характеристики типовых регуляторов приведены в табл. 5.1.

Типовые законы регулирования являются близкими к оптимальным при управлении объектами с запаздыванием, описывается передаточными функциями первого и второго порядка. Однако получить переходную характеристику вида рис. 5.4, соответствующего звену чистого запаздывания не удается.

При рассмотренных передаточных функциях объектов и полученных для них типовых законах регулирования передаточная функция разомкнутой системе в соответствии с (5.5) во всех случаях определяется выражением

Логарифмические амплитудная и фазовая характеристики для таких систем изображены на рис. 5.5.

Рис. 5.5

Фазовая характеристика описывается выражением:

(5.17)

и на частоте среза 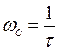фазовый сдвиг достигает -147 град, что обеспечивает запас по фазе только 33 градуса и 50 % перерегулирования переходной характеристики.

Таблица 5.1

Тип регулятора	Передаточная функция	Логарифмическая частотная характеристика	Переходная функция
П
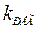
И
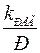
ПИ
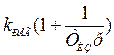
ПД
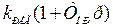
ПИД		2kРЕГ

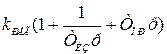
Соответственно переходный процесс отличается от предполагаемого (рис. 5.4), так как на частоте среза разомкнутой системы 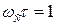, а при определении законов регулирования в разложении 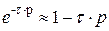ограничивались лишь линейными членами, что справедливо при wt << 1.

Понятно, что такой вариант оптимизации не подходит для промышленных объектов, и не только для них. Оптимизация на минимум квадрата ошибки всегда приводит к выбору параметров вблизи границе устойчивости и сильной колебательности процессов. Рекоменбуется в контур управления ввести дополнительный коэффициент от 0.35 до 0.5, чтобы сделать перерегулирование меньше 5 % и показатель колебательности М = 1.