Анализ и синтез функциональных схем
Функциональные схемы (ФС) предназначены для преобразования логической информации. Исходная информация, закодированная в виде дискретных сигналов, подаётся на входы схемы`хn. Затем данная информация перерабатывается и в дискретной форме считывается с выходов схемы `у m (n, m – числа ее входов и выходов). Рассмотрим ФС, функционирующие в двузначной логике и имеющие один выход (m=1). Преобразование информации в них может быть задано в виде функции алгебры логики у = f(х n). Вместо релейных элементов в ФС используются функциональные элементы (ФЭ), реализующие, как правило, элементарные логические функции.
Определение. Анализом называется построение формулы алгебры логики (если необходимо - ее таблицы истинности) по заданной ФС.
Для построения формулы по заданной схеме необходимо связи между ФЭ в ФС представить в виде подстановок в соответствующие им элементарные функции. При этом предполагается, что переработка информации производится поэтапно от входов к выходам. В реальных схемах для обеспечения временного согласования работы всех ФС используют дополнительные элементы.
Анализ ФС можно выполнять двумя способами – от входов к выходам и от выходов к входам. Рассмотрим первый способ, применяя дополнительные обозначения для промежуточных соединений схемы.
Пример 1. В качестве ФЭ приняты {& ,Ú ,Ø }.Произвести анализ ФС, физическая структура которой дана на рис.1.19.
Решение. Обозначив промежуточные соединения ФЭ так, как показано на рисунке, по шагам определяем сигналы, соотвествующие им. При этом перемещаемся от входов схемы к ее выходу.
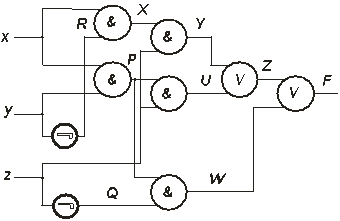
Рис.1.19
ШАГ 1. R =`y , Q = `z.
ШАГ 2. X= x& R = x&`y , P= x& y, W=P&Q = x& y&`z.
ШАГ 3. Y=X& z = x &`y& z , U=P& z = x& y& z.
ШАГ 4. Z = YÚU = x &`y& zÚ x& y& z.
ШАГ 5. F = Z Ú W = x &`y& zÚ x& y& zÚ x& y&`z.
Таким образом, рассмотренная ФС реализует следующую формулу алгебры логики:
F(x, y, z) = x & `y & z Ú x & y & z Ú x & y & `z.
Найденная формула представляет собой СДНФ. Вектор ее значений истинности имеет вид (00000111).
В зависимости от исходных данных, среди задач синтеза (проектирования) ФС можно выделить:
1) синтез схем по заданным формулам,
2) синтез схем по заданным функциям.
Определение. Синтезом ФС по заданной формуле называют построение структуры ФС, соответствующей заданной формуле алгебры логики.
Решение подобных задач производится по алгоритму, обратному методу анализа. Как отмечено в параграфе 1.7, структура формул алгебры логики позволяет изоморфно отобразить только системы с параллельными и последовательными соединениями элементов. Поэтому в ФС, изоморфно соответствующей формуле, должны быть только соединения данного вида.
Определение. Синтезом ФС по заданной функции называют построение структурной схемы, реализующей заданную функцию алгебры логики.
Поскольку представление функций формулами неоднозначно, то данная задача имеет неединственное решение. Как и в случае релейных схем, оптимальными являются ФС, состоящие из минимального количества ФЭ и соединений между ними. Такие ФС можно получить, используя формулы с минимальным числом переменных.
Как и для РС, будем отдельно рассматривать формулы, оптимальные в классе нормальных форм (которые равны соответствующим минимальным формам), а также абсолютно оптимальные формулы, получаемые из минимальных нормальных форм путем их дальнейшего сокращения с применением законов алгебры логики. Способы получения оптимальных формул – те же, что и в релейных схемах. В Примере 1 расcмотрена ФС, реализующая функцию (00000111). Данная ФС не оптимальна, поскольку соответствующая ей формула описывает СДНФ F = x`y z Ú x y z Ú x y`z , которая не является минимальной. Минимизируя её, получим МДНФ следующего вида: F = x y Ú x z. Ей соответствует ФС на рис.1.20
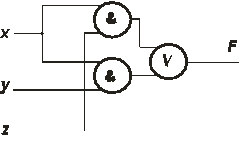
Рис.1.20
Если применить дистрибутивный закон к МДНФ, то получим формулу с ещё меньшим числом переменных: f = x(y Ú z). Для данной функции она совпала с МКНФ. Ей соответствует абсолютно оптимальная схема

Рис.1.21
Очевидно, данная схема значительно проще исходной (рис.1.19). Поскольку синтез оптимальных ФС сводится к построению минимальных формул, то аналогично строятся оптимальные схемы и в других базисах. Аналоги первого и второго дистрибутивных законов алгебры логики для шефферовых и веббовых форм можно получить, заменяя в данных законах:
&( x, y)= Ø ½ ( x, y) = ¯ (Øx,Øy);
Ú ( x, y)= ½ (Ø x, Øy) =Ø ¯ (x, y).
Пример 2. Построить ФС, реализующую одноразрядный двоичный сумматор двух чисел при помощи ФЭ, соответствующих базису {Ø ,¯ } , а также в базисе {¯ }.
Решение. Обозначим одноразрядные двоичные числа, подаваемые на вход, через (х,у). На выходе должна быть получена их суммав двоичной системе. Если х=1, у=1, то S = 210 = 102, поэтому для изображения её в общем случае необходимо использовать два двоичных знака, а ФС должна иметь два выхода. Обозначим их f (старший разряд суммы) и g (младший разряд). Таблицы истинности функций f (х,у), g(х,у):
| x | y | f(x,y) | g(x,y) |
Строим СВНФ функций в базисе {Ø ,¯}. f имеет в векторе истинности одну единицу, поэтому ее форма состоит из одной конституенты: f =¯ (Ø х,Ø у). У функции g СВНФ имеет вид: g =د(¯(х,Ø у),¯(Ø х,у)). Данные формы являются минимальными. При объединении входов элементов функциональную схему можно представить в следующем виде:
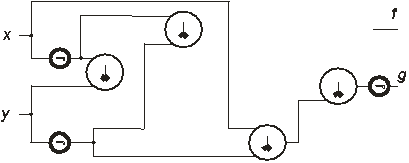
Рис.1.22
В рассмотренном примере невозможно упрощение веббовых нормальных форм при помощи законов алгебры логики. В однофункциональном базисе {¯} ФС получим, применяя подстановку Ø х = ¯ (х,х). Соответствующая схема дана на рис.1.23.
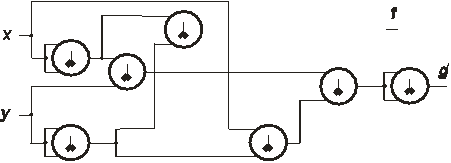
Рис.1.23
ЗАДАЧИ
1. Построить с использованием ФЭ {& ,Ú ,Ø }оптимальные в классе нормальных форм и абсолютно оптимальные ФС, реализующие следующие функции:
а) (x®y)Å zy ;б)(xÅy)|z,в) xy®yz ;г) x|(yÚ z);д) x®(y®z) ;
е) (10011101) ;ж) (01101011) ;з) (1110101111111110).
2. Построить с использованием ФЭ {Ú,Ø }ФС функций 1.а) -ж).
3. Построить с использованием ФЭ {&,Ø }ФС функций 1.а)-ж).
4. Построить ФС, реализующую одноразрядный двоичный сумматор (Пример 2)при помощи ФЭ следующего вида:
а){& ,Ú ,Ø}, б) {Ú ,Ø } , в) {& ,Ø}, г) {x| y}.
5. С помощью ФЭ {& ,Ú ,Ø }построить ФС следующих устройств:
а) преобразователя с двоичными входами (х,у),и выходом f , который работает следующим образом: при подаче х=0на выходе f = у , а при подаче х =1на входе f =`у;
б ) избирательного устройства с двоичными входами (х, у)и выходами f0, f1, f2, f3, который воспринимает на входе комбинацию значений (х у) как двоичное число i, лежащее в интервале от 0 до 3. Значения выходов для каждого i следующие: fi = 1, а все остальные fj = 0, ( 0 £ j £ 3 , j ¹ i ).
6. Можно ли в качестве базиса при построении ФС принять следующие наборы функций:
а) (1001),(10001110),
б) (0101),(1011),(1101),
в) (1010),(01110001)?
Ответ обосновать.
7. Привести примеры управляющих функций, ФС которых нельзя построить только из одних ФЭ типа {®}.
8. Привести примеры управляющих функций, ФС которых нельзя построить только из одних ФЭ типа{ Å , º }.
9. Дана ФС из ФЭ {& ,Ú ,Ø }.
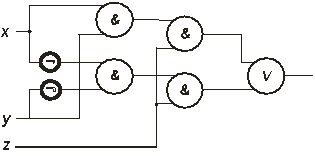
Рис.1.24
Можно ли из нее исключить путем эквивалентных преобразований:
а) все элементы {Ø}?
б) все элементы {&}?
в) все элементы {Ú}?
10. Оптимизировать ФС из ФЭ {& ,Ú ,Ø },приведеную на рис.1.25.
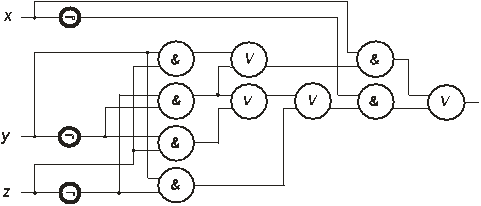
Рис.1.25
Построить ФС:
а) оптимальную в классе нормальных форм и
б) абсолютно оптимальную.
Дата добавления: 2020-10-14; просмотров: 796;











