Оценка погрешностей методов

Все оценки погрешности, полученные для решений задачи Коши для одного дифференциального уравнения 1-го порядка, остаются справедливыми и для решения систем аналогичных дифференциальных уравнений. В силу этого абсолютная погрешность метода Эйлера на каждом шаге пропорциональна величине h²

.

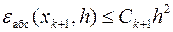Здесь

,

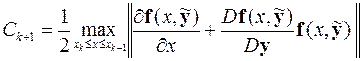где

.

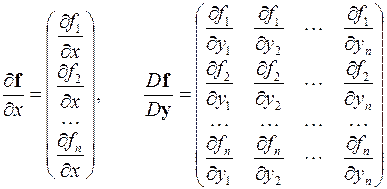При вычислении коэффициента C_k+1 в качестве вектор-функции используется некая промежуточная функция, кривая которой в (n+1)-мерном пространстве переменных x, y₁, y₂,..., y_n, располагается между кривыми приближённого и неизвестного точного решений.

В соответствии с алгоритмом метода Эйлера рас­чётная схема решения системы дифференциальных уравнений может быть представлена в виде следующих соотношений

, .

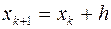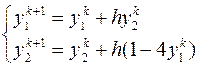Таким образом, процесс решения с заданным шагом интегрирования h = 0.1 будет выглядеть следующим образом

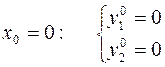
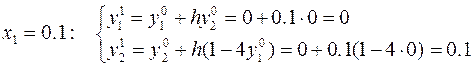
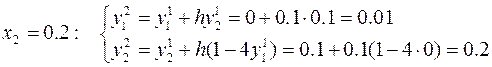
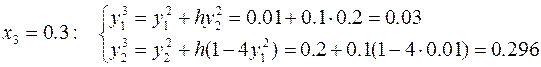
Для получения оценки погрешности решения необходимо повторить про­деланные расчёты с удвоенным шагом h = 0.2

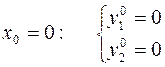
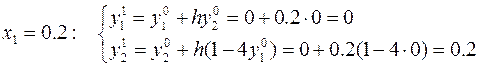
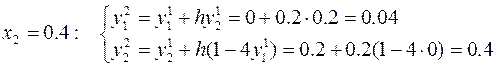
Эти результаты позволяют оценить абсолютную и относительную погрешности решения с шагом интегрирования h = 0.1

,

,

,

,

,

,

,

,

,

,

.

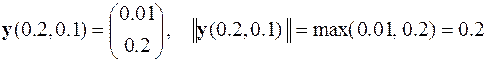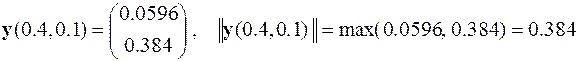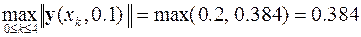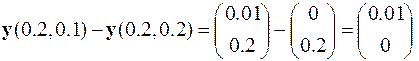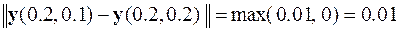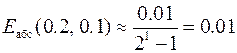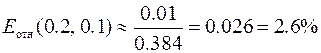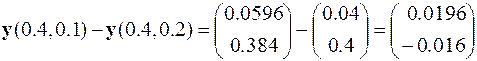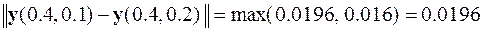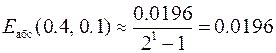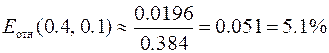Из этих расчётов видно, что решение рассматриваемой задачи Коши методом Эйлера с шагом 0.1 на отрезке [0, 0.4] получено с относительной погрешностью не большей, чем 5.1%.

Возможный вариант реализации усовершенствованного метода Эйлера в программе Excel представлен на рис.5. Здесь решена задача Коши, подобная рассмотренной выше. отличие состоит в том, что отрезок построения решения увеличен до отрезка [0, 1]. Сравнение решений с шагами h = 0.1 и h = 0.05 позволяет оценить погрешность последнего.

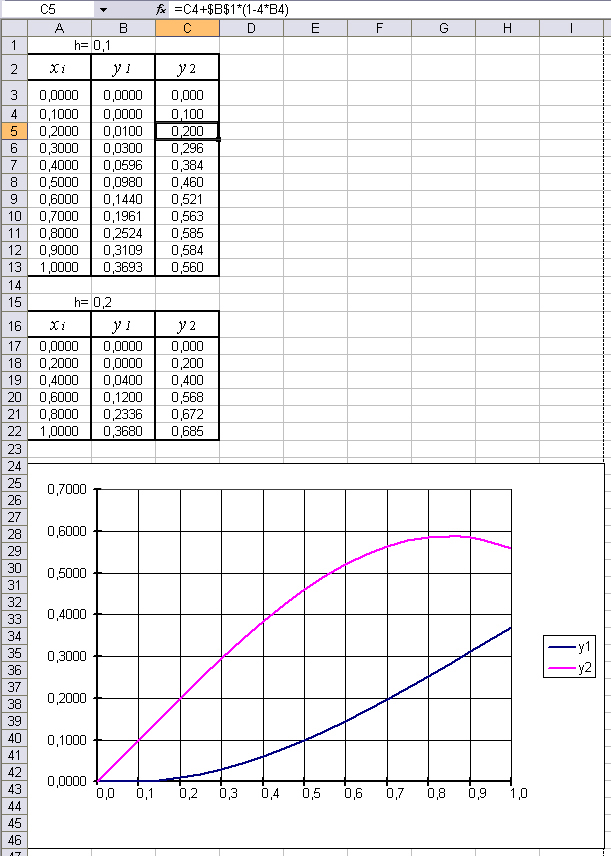
Рис.5.

СПИСОК ЛИТЕРАТУРЫ

1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – 3-е изд., перераб. и доп. М.: БИНОМ. Лаборатория знаний, 2003. 632 с.

2. Воеводин В.А. Вычислительные основы линейной алгебры. М.: Наука, 1977. 303 с.

3. Волков Е.А. Численные методы. М.: Наука, 1982. 254 с.

4. Киреев В.И., Пантелеев А.В. Численные методы в примерах и задачах. М.: Высшая школа, 2004. 480 с.

5. Инженерные расчеты на ЭВМ: Справочное пособие/Под ред. В.А.Троицкого. Л.: Машиностроение, 1979. 288 с.

6. Гельман В.Я. Решение математических задач средствами Excel: Практикум. СПб.: Питер, 2003. 240с.: ил.

7. Васильев, А.Н. Научные вычисления в Microsoft Excel. M.: Издательский дом "Вильяме", 2004. 512 с.: ил

8. Лавренов С.М. Excel: Сборник примеров и задач. - М.: Финансы и статистика, 2003. 336 с.: ил.