Усовершенствованный метод Эйлера

Характерной особенностью метода является использование в качестве направления поиска каждой последующей точки численного решения касательной, определяемой в центре отрезка [x_k, x_k+1]. Как видно на рис.4 для k = 0, последовательно выполняются два шага по методу Эйлера.

Первый из них используется для вычисления тангенса угла наклона касательной в средней точке отрезка [x_k, x_k+1]

,

,

,

.

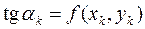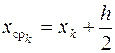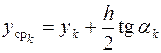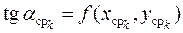После этого делается второй шаг для вычисления x и y новой точки

, .

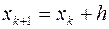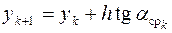Если тангенсы углов наклона касательных заменить на правую часть дифференциального уравнения f(x, y), то вышеприведенные фор­мулы для выполнения одного шага по усовершенствованному методу Эйлера сведутся к следующим

, ,

, .

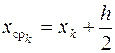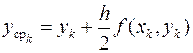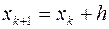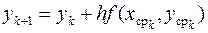Этот метод является методом второго порядка точности. Он даёт меньшую погрешность численного решения на шаге h, чем метод Эйлера. Его абсолютная погрешность ε_абс(x_k+1, h) на каждом шаге пропорциональна величине h³, а решение совпадает с истинным в случае, когда оно представимо квадратичной функцией y = a₁+ a₂x + a₃x². Однако это достигается тем, что его трудоёмкость увеличивается примерно в два раза, поскольку для одного шага приходится два раза вычислять значение правой части дифферен­циального уравнения.