Оценка погрешностей методов

Как уже отмечалось выше, при использовании метода Эйлера на каждом шаге положение следующей точки решения, вычисляется с использованием информации о правой части f(x, y) уравнения только в крайней левой точке отрезка [x_k, x_k+1]. В результате его абсолютная погрешность на каждом шаге пропорциональна величине h²

,

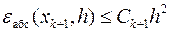где

.

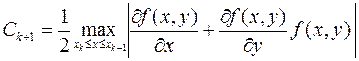В формуле для C_k+1 в качестве функции y используется некая промежуточная функция, график которой располагается между графиками приближённого и неизвестного точного решений.

Аналогичные соотношения для оценки абсолютных погрешностей на каждом шаге можно привести для усовершенствованного метода Эйлера

,

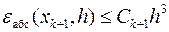где

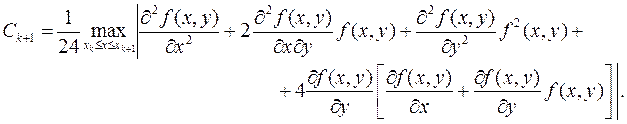
Так как на отрезке интегрирования дифференциального уравнения требуется выполнить несколько шагов, то общая абсолютная погрешность вычисления приближённого решения в точке x_n будет складываться из погрешностей каждого отдельного шага

,

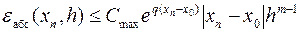где m = 2 для метода Эйлера и m = 3 для усовершенствованного метода Эйлера, а параметры C_max и q определяются следующим образом

, .

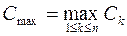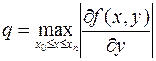Такое вычисление абсолютных погрешностей решения задачи Коши затруднено, так как требует решения дополнительной, зачастую даже более сложной, задачи поиска максимума высших производных правой части уравнения. Поэтому чаще для вычисления погрешности методов используют апостериорные оценки, базирующиеся на правиле Рунге (правило двойного счёта), идея которого описана в лабораторной работе №1. Его основное соотношение, справедливое для всех способов приближённого решения задачи Коши, имеет вид

,

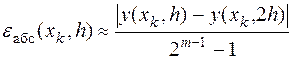где y(x_k, h) и y(x_k, 2h) – приближённые значения решения, вычисленные в точке x_k при шагах интегрирования, отличающихся друг от друга в два раза.

В качестве относительной погрешности решения задачи Коши на отрезке [x₀, x_n] его построения, часто используют её интервальную оценку, равную отношению абсолютной погрешности к максимальному значению модуля решения на данном отрезке

.

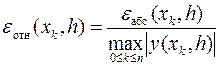Работа методов и оценка погрешности получаемых результатов может быть проиллюстрирована на примере построения приближённого решения задачи Коши для уравнения 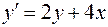с начальным условием y(0) = 0 на отрезке [0, 0.4] с шагом h = 0.1.

1. Решение задачи методом Эйлера. В соответствии с алгоритмом метода рас­чётная схема может быть представлена в виде следующих соотношений

.

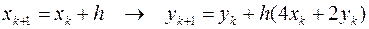Таким образом, пошаговый процесс построения решения с заданным шагом интегрирования h = 0.1 будет выглядеть следующим образом

,

,

,

,

.

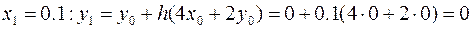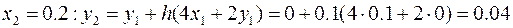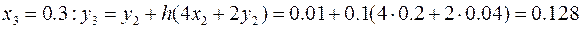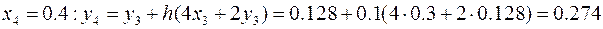Для оценки погрешности полученного решения необходимо повторить про­деланные расчёты с удвоенным шагом интегрирования h = 0.2

,

,

.

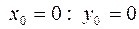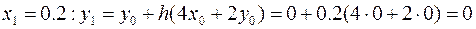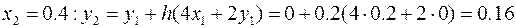Полученные результаты позволяют оценить абсолютную и относительную погрешности решения с шагом интегрирования h = 0.1

,

,

,

.

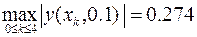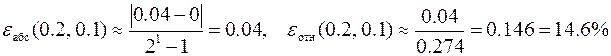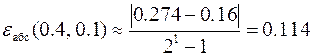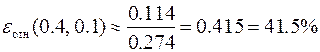2. Решение задачи усовершенствованным методом Эйлера. В данном случае рас­чётная схема метода представляется в виде соотношений

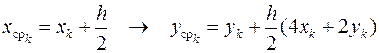
В соответствии с этим процесс построения решения с шагом интегрирова­ния h = 0.1 будет иметь вид

,

,

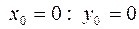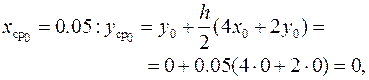
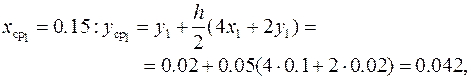
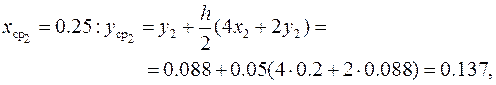
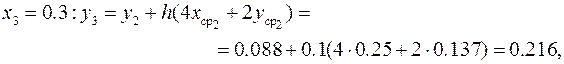
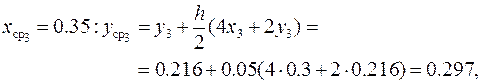
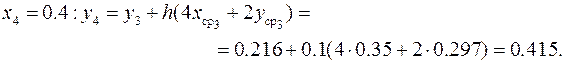
Аналогично предыдущему примеру, где реализован метод Эйлера, для вы­числения погрешности решения с шагом h = 0.1 повторяются расчёты с шагом h = 0.2

,

,

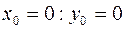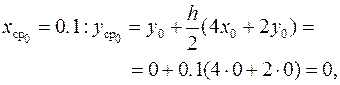
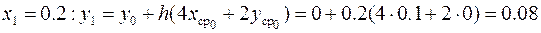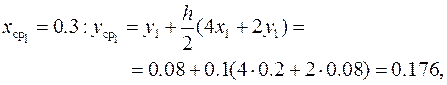
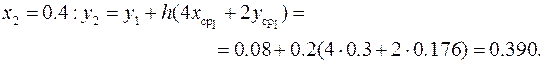
Откуда абсолютная и относительная погрешности решения с шагом h = 0.1будут соответственно равны

,

,

,

,

.

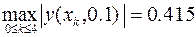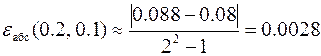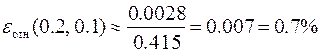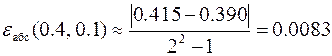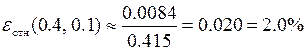Возможный вариант реализации усовершенствованного метода Эйлера в программе Excel представлен на рис.5. Здесь решена задача Коши, подобная рассмотренной выше. Её отличие состоит в том, что отрезок построения решения увеличен до отрезка [0, 1]. Сравнение

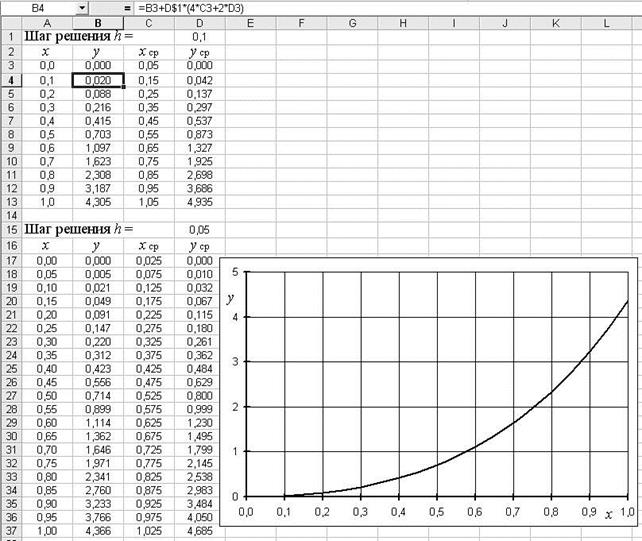
Рис.5.

решений с шагами h = 0.1 и h = 0.05 позволяет оценить погрешность последнего:

при x = 0.5 , ,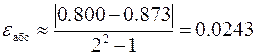

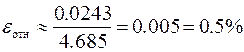при x = 1.0 , ,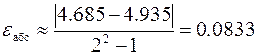

то есть относительная погрешность решения при h = 0.05 имеет оценку сверху в 1.8%.