Взаимодействие молекул. Средняя длина свободного пробега

Столкновением молекул будем называть процесс их взаимодействия, в результате которого изменяются скорости молекул.

Характер взаимодействия молекул можно представить, если рассмотреть зависимость потенциальной энергии взаимодействия молекул от расстояния между их центрами. Эта зависимость имеет вид, приближенно показанный на рисунке 11.2.

Представим, что одна молекула находится в начале координат, а вторая приближается к ней из «бесконечности», имея очень небольшую кинетическую энергию. На расстояниях, превышающих 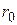_, взаимодействие молекул имеет характер притяжения. Действительно, для 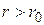с увеличением расстояния между молекулами потенциальная энергия возрастает. Это означает, что ее градиент направлен в сторону увеличения расстояния между молекулами, а сила взаимодействия ( 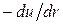) направлена в сторону уменьшения расстояния между молекулами. Поэтому при сближении молекул их взаимная скорость возрастает: потенциальная энергия взаимодействия преобразуется в кинетическую, приближающаяся молекула разгоняется.

На расстояниях менее 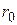притяжение сменяется быстро возрастающим отталкиванием. Потенциальная энергия взаимодействия резко возрастает (кинетическая преобразуется в потенциальную), и при ее равенстве начальной кинетической энергии молекулы останавливаются. Далее происходят обратные процессы, молекулы разлетаются.

Минимальное расстояние d, на которое сближаются при соударении центры молекул, называется эффективным диаметром молекулы. Величина 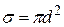называется эффективнымсечениеммолекулы. 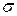равно площади поперечного сечения цилиндра, по оси которого движется данная молекула, такого, что если центр другой молекулы попадает в объем цилиндра, то молекулы должны столкнуться.

Понятно, что при увеличении температуры центры молекул при соударениях будут сближаться сильнее, поэтому эффективный диаметр зависит от температуры. Следует иметь в виду, что рост потенциальной энергии отталкивания происходит очень быстро, поэтому зависимость эффективного диаметра от температуры имеет место обязательно, но выражена не очень сильно.

За секунду молекула проходит в среднем путь, равный ее средней скорости 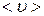. Если за секунду она претерпевает 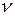столкновений, тосредняядлинасвободногопробега молекулы

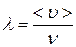(11.9).

Для расчета 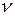предположим, что все молекулы, кроме данной, покоятся на своих местах. Ударившись об одну из неподвижных молекул, данная будет лететь прямолинейно до соударения с другой. Очередное столкновение произойдет в том случае, если центр неподвижной молекулы окажется от прямой, вдоль которой летит данная молекула, на расстоянии меньшим эффективного диаметра. За секунду молекула столкнется со всеми молекулами, центры которых попадают в объем коленчатого цилиндра с основанием 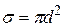и длинной, равной средней скорости 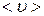. Если концентрация молекул равна n, то число соударений на этом пути

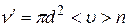(11.9)

Необходимо учесть, что на самом деле движутся все молекулы, и в (11.9) необходимо учитывать не 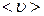, а среднюю относительную скорость движения молекул, которая в 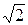раз больше. Тогда для средней длины свободного пробега l можем записать:

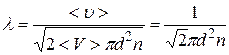(11.10)

Представляет интерес количественная оценка l и 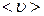. Будем считать, что в жидкости молекулы находятся на небольших расстояниях друг от друга. Тогда корень третьей степени из объема, приходящегося на одну молекулу, даст нам оценку размеров молекулы. Один моль воды занимает объем 18*10^{-10 м3} и содержит число Авогадро 6*10²³ молекул. Тогда на одну молекулу приходится » 30*10^{-30 м3}, а диаметр молекулы » 3*10^{-10 м. При условиях, близких к нормальным, один моль газа занимает объем 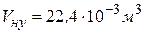. Тогда концентрацию молекул при нормальных условиях можно оценить по формуле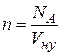} , а среднюю длину свободного пробега в соответствии с формулой (11.10)

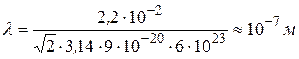
Отметим, что 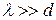, а это означает, что при вычислениях объема коленчатого цилиндра мы справедливо пренебрегли тем, что основания не перпендикулярны оси.

Средняя скорость при нормальных условиях составляет порядка 5*10² м/с. Разделив эту величину на l на, получим оценку количества соударений молекулы в единицу времени: 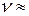=5*10⁹ c^-1.

Вязкость газов

Для понимания физических процессов, обеспечивающих вязкость газов, рассмотрим два соприкасающихся слоя газа толщиной 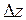, движущихся с различными скоростям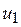и и 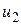. Каждая молекула этих слоев одновременно участвует в двух движениях: тепловом со средней скоростью 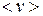и направленном со скоростью 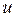, причем 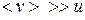. (Скорость теплового движения обычно бывает существенно больше скорости направленного, и мы ограничимся рассмотрением именно этого случая).

В результате теплового движения молекулы одного слоя переходят в другой и наоборот. Оценим количество молекул, пересекающих площадку S между слоями за время 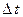в одном направлении в рамках модели, когда 1/6 часть молекул летит в заданном направлении. Площадку пересекают молекулы, которые к началу заданного промежутка времени 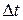находились в цилиндре с основанием S ивысотой в среднем 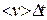, т.е.

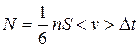. (11.11)

Рисунок 11.4

Такое же количество молекул совершает обратный переход. Попав в другой слой, молекула в результате многочисленных столкновений приходит в равновесие с молекулами нового слоя и либо отдает избыток своего импульса, либо увеличивает свой импульс за счет импульса молекул нового слоя. В результате таких переходов импульс быстро движущего слоя непрерывно уменьшается, а медленно движущегося – растет. Эту ситуацию можно интерпретировать так, что между слоями существует сила взаимодействия, которая один слой ускоряет, а другой – тормозит. Таков механизм взаимодействия слоев.

Произведем количественный расчет. Через площадку S в направлении оси 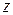за время 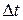переносится импульс:

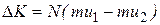(11.12)

Или, с учетом (11.11),

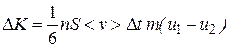(11.13)

Учтем, что в реальном газе скорость при переходе границы раздела между слоями изменится не скачком, а плавно, по некоторому закону 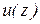. Логично считать, что каждая молекула переносит с собой импульс 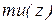, определяемый значением скорости 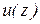в том месте, где произошло ее последнее столкновение перед переходом в новый слой. Естественно также положить, что в среднем последнее столкновение происходит на расстоянии, равном средней длине свободного пробега молекул l. Поэтому молекулам, летящим вдоль оси 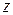, следует приписать скорость 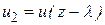, а в противоположном направлении 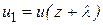. Учитывая, что l является малой величиной можно считать, что

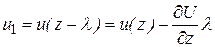
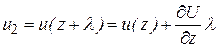. (11.14)

Тогда разность скоростей молекул, совершивших встречные переходы между слоями

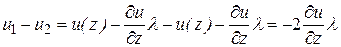. (11.15)

При этом импульс, который переносится молекулами через площадку S за время :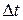

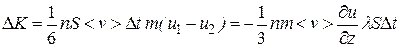(11.16)

Разделив на 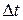, получим для потока импульса (количество через площадку в единицу времени):

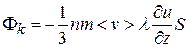(11.17)

Сравнивая соотношение (11.17) с эмпирическим уравнением (11.8):

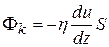
приходим к выводу о том, что (11.17) соответствует эмпирическому уравнению, если положить коэффициент внутреннего трения равным

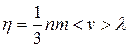(11.18)

Учтем, что произведение 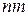дает плотность 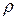газа, и окончательно получим выражение для коэффициент вязкости в рамках молекулярно-кинетической теории:

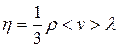(11.19)

Определим, как коэффициент внутреннего трения зависит от параметров газа. Для этого подставим в (11.19) выражения для входящих в него величин:

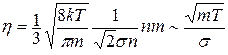(11.20)

Из (11.20) видно, что 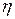зависит только от рода используемого газа (массы молекул, эффективного сечения молекул) и температуры, но не зависит от давления. Это можно легко объяснить. При уменьшении давления уменьшается плотность газа, но пропорционально растет средняя длина свободного пробега. При не очень низких давлениях эти две зависимости компенсируют друг друга.

Однако необходимо иметь в виду, что если давление станет настолько малым, что l превзойдет размеры сосуда, по которому протекает газ, то при дальнейшем уменьшении давления плотность газа будет уменьшаться, а l будет оставаться постоянной. В этих условиях зависимость h(р) будет наблюдаться.

Путем рассуждений, аналогичных проведенных нами для получения эмпирического уравнения вязкости на основе молекулярно-кинетических представлений, можно получить эмпирические уравнения диффузии (закон Фика) и теплопроводности (закон Фурье). При этом молекулярно-кинетическое выражение для коэффициента диффузии имеет вид:

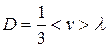(11.21)

А для коэффициента теплопроводности:

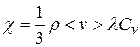(11.22)

Очевидно, что между рассмотренными коэффициентами имеется простая связь:

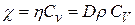(11.20)

Эта связь обусловлена аналогичностью физических процессов, происходящих при наблюдении трех указанных явлений переноса. Различие заключается в том, какая величина переносится между слоями газа.

МИНОБРНАУКИ РОССИИ

Институт сферы обслуживания и предпринимательства (филиал)
федерального государственного бюджетного образовательного учреждения
высшего профессионального образования
«Донской государственный технический университет»
в г. Шахты Ростовской области

(ИСО и П (филиал) ДГТУ)

УТВЕРЖДАЮ

Заведующий кафедрой ЕНД

___________(П.Н. Козаченко)

« 04 » сентября 2013 г.

На правах рукописи

Физика

Конспект лекций

(Часть 3. Электростатика и постоянный ток)

Для студентов направления 230400

«Информационные системы и технологии»

Электронный образовательный ресурс

Составитель: к.ф.-м.н., доцент В.В. Коноваленко

Рассмотрен и рекомендован для использования в учебном процессе на 2013/2014 – 2015/2016 уч. г. на заседании кафедры ЕНД.

Протокол № 1 от 04. 09. 2013 г.

Шахты 2013