Обязательным условием применения критерия Стьюдента является принадлежность выборочных распределений к нормальному (проверено в Л.Р. №2) и статистическое равенство дисперсий.
План выполнения работы:
Пусть Х1 – «Число глаголов в текстах 1 автора», Х2 – «Число глаголов в текстах 2 автора»; причём исправленное сренее квадратическое отклонение для Х1 больше, чем для Х2: (S1>S2).
1. Сформулируйте нулевую H0(об отсутствии существенных различий средних) и альтернативную H1 гипотезы.
2. Докажите статистическое равенство дисперсий, используя критерий Фишера:
а) вычислите 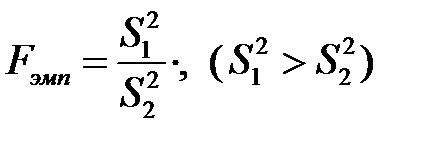 , где
, где 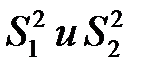 – исправленные выборочные дисперсии;
– исправленные выборочные дисперсии;
б) найдите по таблице критических точек распределения Фишера значение критерия 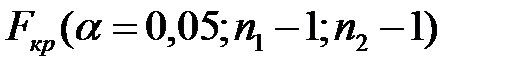 с n1-1 и n2-1 степенями свободы (n1 и n2 – объёмы выборок) и уровнем значимости α=0,05
с n1-1 и n2-1 степенями свободы (n1 и n2 – объёмы выборок) и уровнем значимости α=0,05
в) если 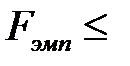
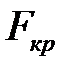 , то различие исправленных выборочных дисперсий статистически не значимо.
, то различие исправленных выборочных дисперсий статистически не значимо.
3. Найдите статистику критерия Стьюдента tв по формуле: 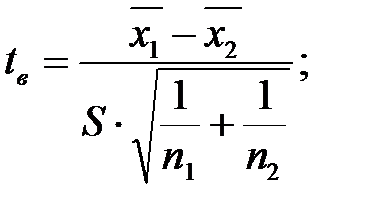 если
если 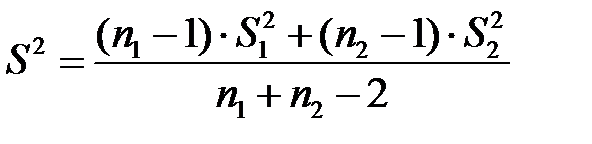 ,
,
где 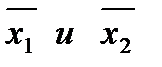 - средние выборочные частоты.
- средние выборочные частоты.
4. Определите число степеней свободы k= 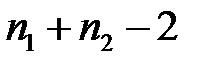
5. Найдите критическое значение tα;k, по таблице квантилей распределения Стьюдента: здесь α – уровень значимости, (обычно α=0,05).
6. Полученное по выборке tв сравнивается с критическим значением tα;k.: если 
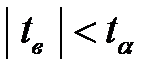 , то гипотеза H0 принимается, в противном случае принимается гипотеза H1.
, то гипотеза H0 принимается, в противном случае принимается гипотеза H1.
Если же дисперсии статистически не равны, или распределение хотя бы одной генеральной совокупности существенно отличается от нормального,то чаще всего применяют наиболее чувствительный аналог критерия Стьюдента для независимых выборок – критерий U-Манна-Уитни.
С помощью программы SPSS:
В главном окне перейти на вкладку "переменные", ввести имя первой переменной Х, метка – "частота употребления глаголов", шкала – "количественная". Вторая переменная: имя – Y, метка – "автор". Введём значения меток Y: значение 1, метка – фамилия первого автора → добавить; значение - 2, метка - фамилия второго автора→добавить; установить шкалу – "номинальная".
Перейти на вкладку "данные", поместить в столбик Х частоты употребления глаголов для первого и второго автора, а в столбик Y – 1 –для первого автора и 2 – для второго.
Анализ → сравнение средних → T-критерий для независимых выборок. В открывшемся диалоговом окне переместить Х в окно "Проверяемые переменные", а Y – в окно "группировать по…", выбрать вкладку "задать группы": группа 1→1; группа 2 →2. Продолжить. Открыть вкладку "Параметры", поставить доверительный интервал 95%→продолжить→ОК
В окне вывода получаем значение t-критерия и значимость. Если значимость не превышает 0,05, то отличие средних значений частот употребления глаголов двух авторов статистически значимо.
Дата добавления: 2016-06-05; просмотров: 2234;











