Однофакторный дисперсионный анализ. Исследование влияния стиля речи на частоту употребления глагольных форм.

Цель: Научиться применять однофакторный дисперсионный анализ для проверки влияния независимой лингвистической СВ (номинативный признак) на зависимую СВ, измеренную в метрической шкале, для дальнейшего использования метода в социо-лингвистическом анализе.

Дисперсионный анализ (сокращённое обозначение ANOVA от Analysis Of Variance) – это метод проверки зависимости нормально распределённой случайной величины (результативный признак) от нескольких величин (факторы) [19, c.189-193]. ANOVA был разработан Р. Фишером специально для анализа результатов экспериментальных исследований. В зависимости от плана исследования выделяют четыре основных варианта ANOVA: однофакторный, многофакторный, ANOVA с повторными измерениями, многомерный ANOVA.

Однофакторный ANOVA - проверка влияния на результативный признак одного контролирующего фактора, имеющего несколько уровней (градаций).

Математическая идея ANOVA основана на соотнесении межгрупповой и внутригрупповой частей дисперсии (изменчивости) результативного признака. В модели ANOVA внутригрупповая изменчивость рассматривается как обусловленная случайными причинами, а межгрупповая – как обусловленная действием изучаемого фактора на результативный признак. Чем больше отношение межгрупповой изменчивости к внутригрупповой, тем выше факторный эффект: тем больше различаются средние значения, соответствующие разным градациям фактора.

Основные допущения ANOVA:

ü нормальное распределение результативного признака (не оказывает большого влияния на результат);

ü гомогенность (равенство) дисперсий выборок, соответствующих разным градациям фактора (при равенстве объёмов выборок несущественно);

ü независимость выборок, соответствующих разным градациям фактора (обязательное условие).

За показатель изменчивости берётся сумма квадратов отклонений значений выборки от среднего выборочного (обозначается SS – Sum of Squares) 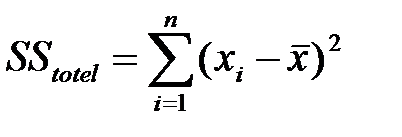(totel – общая)

Общегрупповая изменчивость равна сумме внутригрупповой 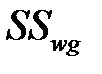(Within-Group) и межгрупповой 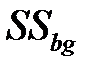(between-group):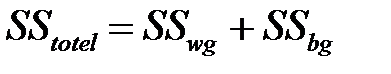

Межгрупповая изменчивость 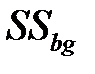– показатель изменчивости между k группами (каждая численностью n объектов) вычисляется

по формуле: ,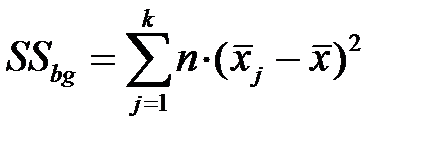

где 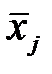-среднее значение для группы j, а 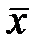– общее среднее.

Коэффициент детерминации 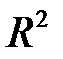– отношение межгрупповой и общей суммы квадратов, показывает, какая доля общей дисперсии результативного признака обусловлена влиянием фактора.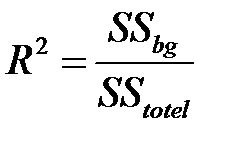

Внутригрупповая сумма квадратов 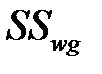‑ показатель случайной изменчивости (внутри групп)

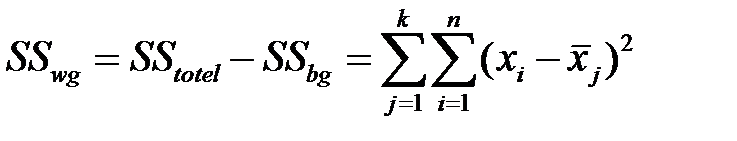
Число степеней свободы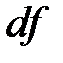

для общей суммы квадратов : ;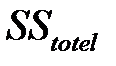

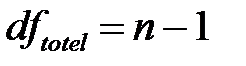для межгрупповой суммы квадратов : ;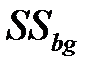

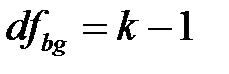для внутригрупповой суммы квадратов : .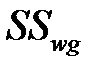

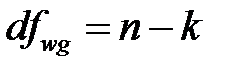Средние суммы квадратов ‑ межгрупповой и внутригрупповой

средний квадрат: ;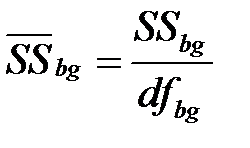

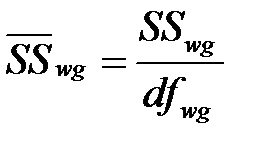
Основным показателем ANOVA является F-отношение – эмпирическое значение критерия Фишера:

;

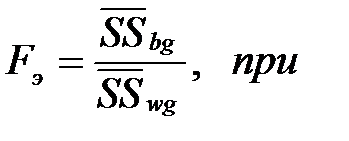
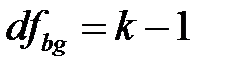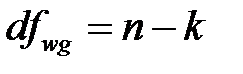
При вычислении «вручную» для вычисления р-уровня значимости применяются таблицы критических значений F-распределения для направленных альтернатив (односторонний критерий).

Для выполнения работы студенты проводят предварительную подготовку: выбирают по 5 фрагментов в 100 словоупотреблений различных стилей речи: художественного (из художественного повествования автора в литературном произведении), публицистического (из газетной статьи) и научного (из научной статьи). Подсчитывают количество глагольных форм (Y) в каждом фрагменте. Данные оформляются в виде таблицы:

Результативный признак Y – «число употребления глагольных форм»; группирующий признак (фактор), имеющий три уровня (градации) – «стиль речи».

Необходимо проверить на уровне значимости р=0,05 гипотезу о зависимости числа употребления глагольных форм от стиля речи.

План выполнения работы:

1) Сформировать нулевую Н₀ и альтернативную Н₁ гипотезы.

(нулевая гипотеза содержит утверждение о равенстве средних значений результативного признака на всех уровнях фактора, альтернативная – утверждение о различие по крайней мере двух средних значений).

2) Найти общее среднее 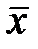и групповые средние: , , .

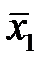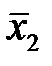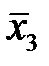3) Вычислить суммы квадратов отклонений значений выборки от среднего :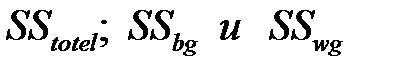

4) Определить числа степеней свободы: ; ; .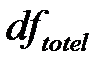

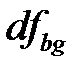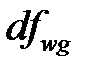5) Найти средние квадраты отклонени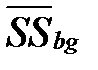й: и .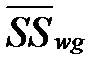

6) Вычислить эмпирическое F-отношение: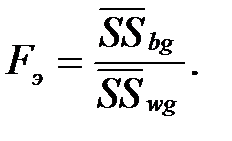

7) По таблице 5 критических значений F-распределения (распределение Фишера-Снедекора) найти уровень значимости с найденным числом степеней свободы числителя 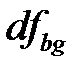и числом степеней свободы знаменателя .

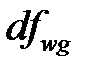8) Сделать вывод относительно принятия или опровержения гипотез Н₀ и Н_1, и качественный вывод о статистической зависимости или независимости частот употребления глаголов от стиля речи.

Для решения задачи в программе SPSS:

ü открыть программу SPSS, в главном окне перейти на вкладку "переменные", ввести следующие переменные:

N (номер), числовая переменная, шкала порядковая;

Y (число глаголов), числовая переменная, шкала количественная;

Х (стиль речи), числовая переменная, шкала номинальная.

Установить метки значений Х: 1‑ «худож», 2‑ «публиц», 3‑ «научн», перейти в окно "данные" и ввести исходные значения переменных;

ü выбрать "Анализ"→ "Сравнение средних" → "Однофакторный дисперсионный анализ";

ü перенести в окно "зависимые переменные" переменную Y, а в окно "фактор" переменную Х (стиль речи);

ü открыть вкладку "параметры" и отметить "описательные", "проверка однородности дисперсии" и "график средних" → "продолжить" →ОК.

Получаем: а) описательные статистики; б) критерий однородности дисперсии по статистике Ливиня (если уровень значимости (Знч) больше 0,05, то отличие дисперсий статистически не значимо;

в) дисперсионный анализ (если уровень значимости не превышает 0,05, то отличия средних значений в группах статистически значимо);

г) график зависимости среднего значения количества глаголов от стиля речи.

Список рекомендуемой литературы

1. Вентцель Е.С. Теория вероятностей. М.: КноРус, 2010.

2. Виноградов О. П. ЧТО ТАКОЕ ЗАКОН БОЛЬШИХ ЧИСЕЛ. М.:СУНЦ МГУ, 2008.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшее образование, 2009.

4. Головин Б.Н. Язык и статистика. М., «Просвещение», 1971.

5. Кремер Н.Ш. Теория вероятностей и математическая статистика: учебник для вузов. М.:ЮНИТИ_ДАНА, 2009.

6. Наследов А.Д. Математические методы психологического исследования. Анализ и интерпретация данных. Учебное пособие. – СПб.: Речь, 2004.

7. Наследов А.Д. SPSS: компьютерный анализ данных в психологии и соц. науках / А.Д.Наследов. - СПб.: Питер Принт, 2005.

8. Письменный, Д.Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам. -М.: Айрис-пресс, 2006.

9. Пиотровский Р.Г., Бектаев К.Б., Пиотровская А.А. Математическая лингвистика. Учебное пособие для пед. ин-тов. М., «Высш. Школа», 1997.

Список использованной литературы

1. Алефиренко, Н.Ф. Современные проблемы науки о языке [Текст]: учебное пособие. М.: Флинта: Наука, 2005.

2. Арапов, М.В., Херц М.М. Математические методы в исторической лингвистике. М.: «Наука», 1974.

3. Бектаев К.Б., Пиотровский Р.Г. Математические методы в языкознании. Ч.2. Математическая статистика и моделирование текста. Алма-Ата, 1974

4. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. М.: Наука,1983.

5. Вентцель Е.С. Теория вероятностей. М.: КноРус, 2010.

6. Виноградов О. П. ЧТО ТАКОЕ ЗАКОН БОЛЬШИХ ЧИСЕЛ. М.:СУНЦ МГУ, 2008.

7. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшее образование, 2009.

8. Гнеденко Б.В., Хинчин А.Я. Элементарное введение в теорию вероятностей. – М.: Наука, 1982.

9. Головин Б.Н. Язык и статистика. М., «Просвещение», 1971.

10. Гресс П.В. Математика для гуманитариев. Учебное пособие. – М.: Логос, 2004.

11. Зайкин М.И. О диалектике профессионального и общекультурного в математической подготовке гуманитариев. Материалы Всероссийской научно- практической конференции. Москва-Коряжма., 2005.

12. В.А. Звегинцев. История языкознания XIX и XX веков в очерках и извлечениях., ч. 1. М., 1964.

13. Колемаев В.А., Калинина В.Н., под ред. В.А. Колемаева. Теория вероятностей и математическая статистика. Учебник :– М.: ИНФРА-М, Высшее образование, 1997.

14. Кремер Н.Ш. Теория вероятностей и математическая статистика: учебник для вузов. М.:ЮНИТИ_ДАНА, 2009.

15. Колмогоров А.Н., Журбенко И.Г., Прохоров А.В. Введение в теорию вероятностей. - М.: Физматлит, 1995.

16. Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко В.А. Сборник задач по высшей математике. 2. – М., Айрис-Пресс, 2004.

17. Мхитарян В.С., Астафьева Е.В., Миронкина Ю.Н., Трошин Л.И. Теория вероятностей и математическая статистика. – М.: Московская финансово-промышленная академия, 2011.

18. Невельский П.Б. Объём памяти и количество информации. Сб. Проблемы инженерной психологии. психология памяти. Вып. 3. Л.,1965.

19. Наследов А.Д. Математические методы психологического исследования. Анализ и интерпретация данных. Учебное пособие. – СПб.: Речь, 2004.

20. Наследов А.Д. SPSS: компьютерный анализ данных в психологии и соц. науках / А.Д.Наследов. - СПб.: Питер Принт, 2005.

21. Письменный, Д.Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам. -М.: Айрис-пресс, 2006.

22. Пиотровский Р.Г., Бектаев К.Б., Пиотровская А.А. Математическая лингвистика. Учебное пособие для пед. ин-тов. М., «Высш. Школа», 1977.

23. Письменный Д.Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам.– М., Айрис-Пресс, 2004

24. Пятков А.В. Статистические методы анализа данных для гуманитариев.- Архангельск: Поморский унивеситет, 2007.

25. Солнцев В.М. Язык как системно-структурное образование. 2 изд. М., 1977.

26. Черенков Н.И. Учебное пособие по курсу «Математика». Северо- Западная академия государственной службы, г.Северодвинск, 2006.