Критерий Колмогорова-Смирнова.
Позволяет оценить вероятность того, что данная выборка принадлежит генеральной совокупности с нормальным распределением. Если эта вероятность p<0,05, то эмпирическое распределение существенно отличается от нормального, если p>0,05 то делают вывод о приблизительном соответствии данного эмпирического распределения нормальному.
В пакете анализа данных SPSS:
Анализ> Непараметрические критерии > Одновыборочный Колмогорова-Смирнова.
В открывшемся диалоговом окне переносим Х в окно `Проверяемые переменные`, в окне `Проверяемое распределение` ставим флажок в квадратике `Нормальное`.НажимаемОк.
В полученной таблице находим значение критерия ZКолмогорова-Смирноваи асимптотическую значимость (Асимпт.знч).
Если `Асимпт.знч` больше 0,05, то существенного отличия от нормальности не обнаружено.
 4. Критерий Пирсона
4. Критерий Пирсона
Критерий Пирсона наиболее часто употребляемый критерий для проверки гипотезы о законе распределения.
Для проверки нормальности распределения СВ Х-«Число глаголов в фрагменте из текста выбранного автора длиной 100 словоупотреблений» по выборке вручную воспользуемся следующим планом:
1. Сформировать нулевую H0(о том, что генеральная совокупность распределена по нормальному закону) и альтернативную H1 гипотезу.
2. Выбрать уровень значимости ( чаще всего α=0,05).
3. В полученном предварительно, интервальном статистическом ряде, объединить интервалы, количество наблюдений в которых меньше 5 (необходимым условием применения метода Пирсона является наличие в каждом интервале не менее 5 наблюдений, ni≥5)
4.  Найти параметры, определяющие нормальный закон распределения (а ; σ). Их оценки, вычисленные по выборке,
Найти параметры, определяющие нормальный закон распределения (а ; σ). Их оценки, вычисленные по выборке,
5. Так как нормально распределённая случайная величина определена на (-∞,∞), то заменить крайние интервалы на интервалы
вида (-∞; х1) и (хk-1,∞).
6. Рассчитать вероятность попадания СВ в каждый в каждый из интервалов по формуле 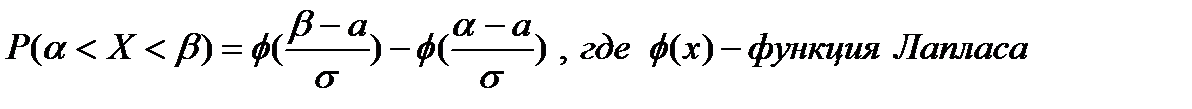 .
.
| хi | ||||
| ni | ||||
| npi |
7. Для каждого интервала найти произведение npi (теоретическая частота).
Полученные результаты занести в таблицу :
8. Найти 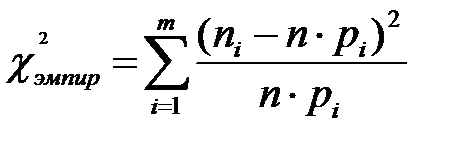 (эмпирическое значение критерия Пирсона).
(эмпирическое значение критерия Пирсона).
9. Вычислить число степеней свободы по формуле k=m-r-1 , где m-число интервалов ряда, r- число параметров предполагаемого распределения (для нормального r=2).
10. По таблице 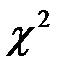 -распределения найти критическую точку
-распределения найти критическую точку 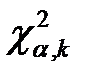 .
.
11. Сделать вывод о принятии или опровержении гипотезы H0.
(если 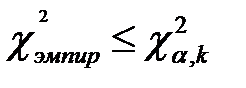 , то гипотеза H0принимается, если
, то гипотеза H0принимается, если 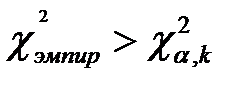 , то H0- отвергается) [25].
, то H0- отвергается) [25].
С использованием программы SPSS:
Анализ> Непараметрические критерии > Хи-квадрат…
В открывшемся диалоговом окне переместить Хв раздел `Проверяемые переменные`>OK
В полученном окне вывода получаем значение критерия Пирсона, найденное по выборке. Сравнить полученное значение с критическим и сделать вывод.
Дата добавления: 2016-06-05; просмотров: 2517;











