ЛЕКЦИЯ 8. Распознавание языков. Язык ВЫПОЛНИМОСТЬ.
Язык – это множество слов над некоторым алфавитом. Как и всякое другое множество, язык можно определить с помощью характеристической функции (формулы). Алгоритмически проблему распознавания можно сформулировать так: построить машину Тьюринга, вычисляющую характеристическую функцию данного языка. Для удобства определим характеристическую функцию произвольного языка следующим образом:
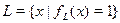
x ÏL при fL(x)≠1 (например, fL(x) =0)
В этом определении под х следует понимать произвольное слово, записанное с помощью символов алфавита языка.
Определение. Машина Тьюринга распознает язык L, если она вычисляет характеристическую функцию данного языка.
Распознающую машину Тьюринга можно построить так, что она будет иметь два конечных состояния, условно обозначаемые как “ДА” и “НЕТ”. Завершение вычислений в состоянии ДА означает, что входное слово распознано как принадлежащее данному языку; в противном случае – как не принадлежащее.
Важной особенностью распознающей машины Тьюринга является то, что она не изменяет в общем случае входное слово. Следовательно, правила такой машины несколько отличаются от правил тех машин, которые мы ранее рассматривали.
Вспомним, как мы определяли правила машины Тьюринга. Для этого мы вводили таблицу вида (например)
| e | |||
| Q0 | ULQ0 | 0LQ0 | UUQ1 |
В этой таблице определены три правила (по количеству ячеек). Внутри ячейки размещается операционная часть правила. Строка и столбец, определяющие ячейку, содержат условную часть правила. Условная часть просто сообщает, в какой ситуации следует применить правило. Например, условная часть (Q0,0) соответствующая первой строке и первому столбцу говорит: ”Если машина находится в состоянии Q0 и читает символ 0, то следует выполнить действие ULQ0”.
Так вот, операционная часть распознающей машины не содержит в общем случае операции записи нового символа (хотя имеется целый класс распознающих машин, которые используют операцию записи, правда, не вместо текущего символа).
Рассмотрим пример следующей машины
| e | |||
| Q0 | LQ0 | QДА | QНЕТ |
Посмотрим, какэта машина принимает слово 00100. До тех пор, пока не встретится первая единица, машина будет находиться в состоянии Q0. Как только встретится первая единица, машина завершит работу в состоянии ДА. Теперь нетрудно сообразить, что данная машина распознает язык, не содержащий полностью нулевых слов. Обратите внимание на правила машины Тьюринга.
Пример. Пусть алфавит языка есть {0,1}. Характеристическая функция fL(x) языка задается следующим образом:
fL(x)=1, если в слове х содержится три и более “1”
fL(x) =0 в противном случае.
Нетрудно построить программу (алгоритм) для вычисления характеристической функции этого языка. Это говорит о том, что представленный язык распознаваем.
Важным понятием в теории распознавания языков является понятие недетерминированной машины Тьюринга.
Вспомним, как мы определяли правила машины Тьюринга. Для этого мы вводили таблицу вида (например)
| e | |||
| Q0 | ULQ0 | 0LQ0 | UUQ1 |
В этой таблице определены три правила (по количеству ячеек). Внутри ячейки размещается операционная часть правила. Строка и столбец, определяющие ячейку, содержат условную часть правила. Условная часть просто сообщает, в какой ситуации следует применить правило. Например, условная часть (Q0,0) соответствующая первой строке и первому столбцу говорит: ”Если машина находится в состоянии Q0 и читает символ 0, то следует выполнить действие ULQ0”.
Но могут существовать машины, в которых допускается применять любое из нескольких возможных правил с одинаковой условной частью. Например, построим следующую таблицу
| e | |||
| Q0 | ULQ0 UUQНЕТ | 0LQ0 | UUQДА |
Теперь в ячейке (Q0, 0) имеется два правила. Какое из этих правил использовать? В принципе, - любое. С точки зрения распознавания языка можно сказать, что если имеется последовательность применения правил таблицы на данном входе, которая завершается в конечном принимающем состоянии, то данное входное слово принадлежит рассматриваемому языку.
Для иллюстрации сказанного рассмотрим следующий пример
| e | |||
| Q0 | LQ0 LQ1 | LQ1 | QНЕТ |
| Q1 | QДА | LQ0 | QНЕТ |
Рассмотрим входное слово 000. Теперь уже машина может сразу же выполнить правило
LQ1. После этого на втором такте может завершить работу в состоянии ДА. Кроме того, можно убедиться, что машина принимает все слова, заканчивающиеся на 10, которой может предшествовать группа из подряд идущих нулей.
Определение. Машина Тьюринга называется недетерминированной, если и только если она содержит два или более правил с одинаковой условной частью и различными операционными частями.
Замечательным фактом является следующий (доказанный выше). Для всякой недетерминированной распознающей машины Тьюринга можно построить эквивалентную ей детерминированную машину.
В практическом плане важным языком является язык ВЫПОЛНИМОСТЬ. Словами этого языка являются дизъюнкты. Примерами дизъюнктов являются следующие:
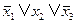
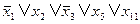
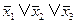
и т.д.
Здесь хi являются булевскими переменными. Булевская переменная может принимать только два значения: 0, 1. Черта сверху над переменной означает ее отрицание. Правила отрицания таковы:
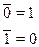
Значок v называется операцией логическое “ИЛИ” (а также дизъюнкцией). Эта операция дает в результате единицу, если и только если хотя бы одна из участвующих в ней переменных равна 1. Таким образом, дизъюнкт 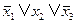 равен 1 при значениях переменных, представленных в следующей таблице
равен 1 при значениях переменных, представленных в следующей таблице
| x1 | x2 | x3 |
Набор логических значений для переменных называется интерпретацией. Интерпретация, при которой дизъюнкт равен 1, называется выполняющейинтерпретацией.
Задача ВЫПОЛНИМОСТЬ заключается в следующем. Имеется множество дизъюнктов. Спрашивается, имеется ли для этого множества дизъюнктов хотя бы одна общая выполняющая интерпретация? Если ДА, то множество дизъюнктов называется выполнимым. Если НЕТ, то множество дизъюнктов называется невыполнимым. Эта задача имеет только кажущуюся простоту. На самом деле, проблема упирается в отыскание эффективного алгоритма ее решения, которую мы рассматриваем на следующем практическом занятии.
Язык ВЫПОЛНИМОСТЬ содержит множество слов, представляющих все выполнимые системы дизъюнктов.
Проблема распознавания языка ВЫПОЛНИМОСТЬ связана с распознаванием выполнимости данной системы дизъюнктов. Если система дизъюнктов выполнима, то это легко проверить, используя значения переменных выполняющей интерпретации. Проверку можно реализовать на недетерминированной в общем случае машине Тьюринга.
Проверка просто устанавливает, удовлетворяет ли найденное решение условиям задачи.
Сложностью проверки называется функция для числа тактов проверочной процедуры в зависимости от длины описания задачи (размера описания задачи). Оказывается, по критерию сложности все машины Тьюринга можно разделить на два класса: машины с функцией сложности, ограниченной некоторым полиномом и машины с функцией сложности, не ограниченной полиномом. Первый тип машин называется также эффективным.
Язык ВЫПОЛНИМОСМТЬ знаменит в силу следующего обстоятельства. Он является универсальным в некотором классе языков. Поэтому определим этот класс, кстати, весьма представительный.
Класс NP (NP – Nondeterministic Polynomial) – это класс языков с процедурой проверки, реализуемой за полиномиальное время на недетерминированной машине Тьюринга. Имейте в виду, что любой детерминированный алгоритм есть частный случай недетерминированного алгоритма.
Определение. Задача А эффективно сводится к задаче В, если
1) Решение задачи B дает решение задачи А;
2) Сложность сведения ограничена полиномиальной функцией.
Примеры сведений.
Задача ВЫПОЛНИМОСТЬ эффективно сводится к задаче 3-ВЫПОЛНИМОСТЬ. Задача 3-ВЫПОЛНИМОСТЬ – это задача ВЫПОЛНИМОСТЬ, каждый дизъюнкт которой содержит не более 3-ех переменных. Рассмотрим на пример, как эта сводимость реализована.
Пусть дана система дизъюнктов
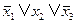
S= 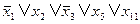
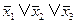
Здесь только второй дизъюнкт содержит более 3 переменных. Заменим второй дизъюнкт, как показано ниже:
S1= 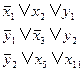
Можно усмотреть следующий общий прием. Мы вводим дополнительную переменную в каждый дизъюнкт, содержащий более трех переменных. Затем отсчитываем три литеры и переносим оставшиеся переменные в новый дизъюнкт. В перенесенном дизъюнкте мы добавляем новую литеру, но уже с отрицанием и т.д.
Задание 6. Доказать, что системы S и S1 эквивалентны.
Указание. Доказательство можно провести с помощью таблицы истинности. Для этого следует ввести понятие таблицы истинности. В нашем случае такую таблицу следует заметно укоротить до
| y1 | y2 |
Возьмем любую строчку из этой таблицы и подставим ее в S1. Ясно, что из выполнимости полученной новой системы автоматически будет следовать выполнимость системы S.
Наоборот, допустим, что система S выполнима, а S1 – невыполнима. Это значит, что как минимум один дизъюнкт в S1 не выполним. Такой дизъюнкт всегда содержит хотя бы одну новую переменную. Дадим этой переменной значение 1. По этому способу можно добраться до последнего дизъюнкта. Завершите эту схему рассуждений.
Задача о паросочетаниях сводится к задаче ВЫПОЛНИМОСТЬ.
Пусть имеется 5 девушек a,b,c,d,e и пять парней x,y,z,w,u. В следующей матрице 1 на пересечении строки i и столбца j означает взаимную симпатию, а 0 – в лучшем случае безразличие. Следует подобрать 5 пар, взаимно симпатизирующих друг другу.
| a | b | c | d | e | |
| x | |||||
| z | |||||
| y | |||||
| u | |||||
| w |
Дата добавления: 2022-02-05; просмотров: 536;











