Операция устранения литеры
Рассмотрим следующую систему дизъюнктов:
| S= | 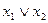 (a) (a)
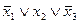 (b) (b)
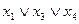 (c) (c)
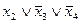 (d) (d)
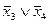 (e) (e)
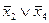 (f) (f)
| (11.1) |
Операция резолюции (резолюционирования) двух дизъюнктов, содержащих контрарную пару литер, скажем 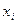 и
и 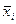 , состоит в порождении резольвенты – дизъюнкта, в котором присутствуют все литеры, входящие в родительские дизъюнкты, кроме
, состоит в порождении резольвенты – дизъюнкта, в котором присутствуют все литеры, входящие в родительские дизъюнкты, кроме 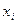 и
и 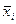 .
.
Пример. Пусть 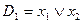 ,
, 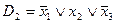 . Их резольвентой будет дизъюнкт
. Их резольвентой будет дизъюнкт 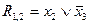 (
( 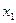 и
и 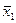 устранены).
устранены).
Можно показать, что резольвента 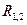 есть логическое следствие из
есть логическое следствие из 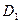 и
и 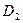 , т.е.
, т.е.
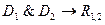 .
.
Следовательно, в силу постулата 1, п. 1c присоединение резольвент к системе не увеличивает ее сложность (т.е. не приводит к увеличению числа инфов). Более того, отбрасывание части дизъюнктов при этом еще более упрощает задачу. Оказывается, можно полностью избавиться от какой-нибудь литеры 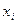 (
( 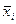 ), перейдя от системы S к новой системе
), перейдя от системы S к новой системе 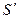 , которая не содержит ни
, которая не содержит ни 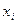 , ни
, ни 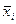 , но эквивалентна S в следующем смысле (в смысле H-эквивалентности): S и
, но эквивалентна S в следующем смысле (в смысле H-эквивалентности): S и 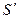 H-эквивалентны, если и только если:
H-эквивалентны, если и только если:
(a) 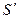 записана с помощью собственного подмножества литер S;
записана с помощью собственного подмножества литер S;
(b) любая выполняющая интерпретация для S содержит выполняющую интерпретацию для 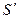 , а любая выполняющая интерпретация для
, а любая выполняющая интерпретация для 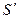 может быть достроена до выполняющей интерпретации для S.
может быть достроена до выполняющей интерпретации для S.
Продемонстрируем все сказанное на системе S (9.1). Перейдем от S к 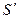 , устранив литеру
, устранив литеру 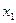 (
( 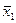 ). Для этого включим сразу в
). Для этого включим сразу в 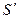 все дизъюнкты из S, не содержащие
все дизъюнкты из S, не содержащие 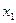 (
( 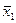 ), т.е. (d, e, f). Для оставшихся дизъюнктов (a, b, c) найдем все возможные резольвенты по
), т.е. (d, e, f). Для оставшихся дизъюнктов (a, b, c) найдем все возможные резольвенты по 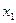 (
( 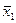 ). Так
). Так 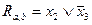 ;
; 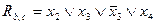 .
.
Присоединим в 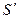 только не тавтологические резольвенты, т.е. не содержащие в своей записи фрагменты
только не тавтологические резольвенты, т.е. не содержащие в своей записи фрагменты 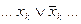
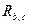 , следовательно, не присоединяется. Другие дизъюнкты в
, следовательно, не присоединяется. Другие дизъюнкты в 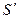 не присоединяются. Итак,
не присоединяются. Итак, 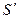 есть следующая система.
есть следующая система.
| S= | 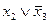
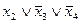
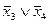
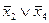
| (11.2) |
Можно доказать, что 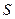 к
к 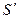 H-эквивалентны. Из наших рассмотрений следует, что сложность
H-эквивалентны. Из наших рассмотрений следует, что сложность 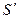 не выше сложности
не выше сложности 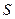 .
.
ПОСТУЛАТ 2.Пусть задачи A и B H-эквивалентны и выполнимы и 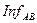 – минимально необходимое и достаточное число инфов, принимаемых во внимание или игнорируемых при сведении задачи A к задаче B. Тогда
– минимально необходимое и достаточное число инфов, принимаемых во внимание или игнорируемых при сведении задачи A к задаче B. Тогда
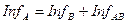 .
.
Следствие.
1. 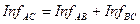 .
.
2. 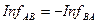 .
.
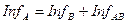 ,
, 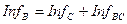 ,
,
откуда
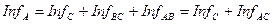 . Заметим, что отрицательное значение числа инфов для процедуры сведения означает, что инфы игнорируются. Ясно также, что эквивалентные преобразования одной задачи в другую не изменяет ее инфологическую сложность.
. Заметим, что отрицательное значение числа инфов для процедуры сведения означает, что инфы игнорируются. Ясно также, что эквивалентные преобразования одной задачи в другую не изменяет ее инфологическую сложность.
Смысл постулата 2 для наших рассмотрений таков. Пусть дана выполнимая задача 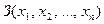 . Постулат 2 позволяет ограничить весь спектр возможных способов решения единственным:
. Постулат 2 позволяет ограничить весь спектр возможных способов решения единственным: 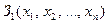 решается как последовательность переходов к H-эквивалентным задачам:
решается как последовательность переходов к H-эквивалентным задачам:
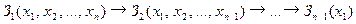 . .
| (11.3) |
Последовательность (11.3) позволяет получить эффективное решение при условии, что если исходная задача содержит полиномиальное (от n) число инфов. Если же задача содержит экспоненциальное (от n) число инфов, то никакие трансформации к H-эквивалентным задачам не позволяют принять во внимание только полиномиальное число инфов при допущении о реалистичности алгоритма. Именно этот факт и позволяет говорить о том, что при экспоненциальном нарастании числа инфов невозможен полиномиальный алгоритм, принимающий во внимание индивидуальные инфы, при условии, которое нами будет установлено на пропускную способность (алгоритма/ЭВМ).
Обозначим TH – пропускную способность алгоритма, N – число выполняемых им шагов при решении задачи, I – число принятых во внимание при этом инфов.
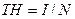 . .
| (11.4) |
ПОСТУЛАТ 3. Какова бы ни была задача A на входе решающего алгоритма, имеет место ограничение пропускной способности алгоритма:
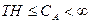 . .
| (11.5) |
где 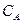 – фиксированная константа.
– фиксированная константа.
Смысл этого постулата состоит в том, что никакой физический вычислитель не может иметь бесконечную скорость обработки информации. Этот постулат связан с физическими ограничениями теории относительности. Данный постулат дает нам следующее: нельзя переработать экспоненциально нарастающее число инфов при ограниченной пропускной способности за полиномиальное число тактов. В самом деле, при допущении обратного следовало бы что
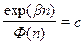 (для любого n),
(для любого n),
где 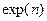 – экспонента от n;
– экспонента от n;
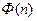 – значение некоторого фиксированного полинома;
– значение некоторого фиксированного полинома;
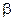 и с – положительные константы.
и с – положительные константы.
Но используя элементарно доказываемое свойство
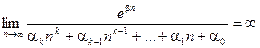
(для этого достаточно взять k производных от числителя и знаменателя), получим противоречие. Следовательно, при индивидуальном анализе инфов и экспоненциально нарастающем числе инфов алгоритм должен тратить экспоненциально растущее число тактов! В дальнейшем мы вынуждены будем ввести в рассмотрение формы – вычисляемые условия, используемые для замены анализа индивидуальных инфов анализом группы инфов.
ПОСТУЛАТ 4.Инфологическая сложность выполнимой задачи Выполнимость 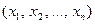 не ниже числа дизъюнктов в минимальной по числу дизъюнктов конъюнктивной нормальной форме, эквивалентной этой задаче Выполнимость.
не ниже числа дизъюнктов в минимальной по числу дизъюнктов конъюнктивной нормальной форме, эквивалентной этой задаче Выполнимость.
В самом деле, все дизъюнкты минимальной КНФ суть инфы по определению. Формулы с меньшим числом инфов для задачи Выполнимость не существует.
Дата добавления: 2022-02-05; просмотров: 396;











