ЛЕКЦИЯ 10. ИНФОЛОГИЧЕСКАЯ СЛОЖНОСТЬ ЗАДАЧ

Для изучения проблемы информационной сложности задач нужно прежде всего оговорить, какие задачи мы будем рассматривать. По очевидным причинам такие задачи должны быть в некотором смысле универсальными, т.е. к ним можно было бы сводить многие другие задачи из некоторого весьма широкого класса задач. Довольно часто в качестве такого класса задач выбирают задачи распознавания свойств, требующие только одного из двух ответов: «Да» или «НЕТ». Кроме того, требуют, чтобы решение задачи можно было эффективно проверить с помощью детерминированного алгоритма. Ранее мы рассматривали задачи сортировки и отмечали, что вычислительная сложность алгоритма сортировки определяется числом сравнений. Если это число растет как некоторый полином от размера исходного массива, то такой алгоритм называется эффективным. Обобщим это определение.

Детерминированный алгоритм называется эффективным, если число выполняемых им операций (не только сравнения) растет как некоторый полином от размера задачи. Под размером задачи понимают, вообще говоря, длину записи задачи при условии, что эта запись неизбыточна.

Итак, найти хорошее решение задачи – значит, построить для нее эффективный детерминированный алгоритм.

Назовем алгоритм недетерминированным, если, по крайней мере, на одном шаге, он допускает различные варианты продолжения работы и нет указаний, какой вариант выбрать.

Недетерминированный алгоритм называется эффективным, если его вычислительная ложность по любой из возможных трасс вычислений не превышает некоторого полинома от размера входной записи.

Так вот, под задачей распознавания свойств будем понимать задачу, такую, что:

(1) она требует ответа «ДА» или «НЕТ»;

(2) решение может быть проверено (если задача его действительно имеет) с помощью полиномиального (эффективного) недетерминированного алгоритма.

Рассмотрим задачу о выполнимости системы логических формул в форме дизъюнктов.

Дизъюнкт – это формула вида

,

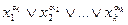(10.1)

где .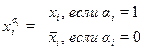

Примером дизъюнктов служат, например, следующие:

,

,

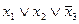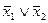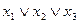и т.д.

Говорим, что дизъюнкт выполним в интерпретации 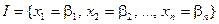, , 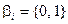если его значением в I служит «1».

Пример. Дизъюнкт 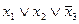выполним в интерпретации 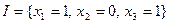, так как .

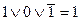Ясно, что число выполняющих интерпретаций для дизъюнкта, содержащего n переменных, составляет 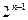и в одной интерпретации он не выполняется.

Задача ВЫПОЛНИМОСТЬ требует дать ответ на вопрос: имеется ли интерпретация I, в которой выполняется каждый из дизъюнктов исходной системы.

Система дизъюнктов задачи Выполнимость называется также конъюнктивной нормальной формой. Среди всех конъюнктивных нормальных форм имеются формы с наименьшим числом дизъюнктов. Такие формы называются минимальными КНФ, эквивалентными данному множеству дизъюнктов.

Эта задача, очевидно, относится к числу задач распознавания. По смыслу вопроса она дает ответ «ДА» или «НЕТ». Если I – некоторая выполняющая интерпретация, то легко проверить (т.е. реализовать эффективный алгоритм проверки), что I выполняет каждый дизъюнкт системы. Эту проверку вполне можно осуществить с помощью детерминированного полиномиального алгоритма.

С. Кук доказал знаменитую теорему о том, что задача Выполнимость является универсальной в классе задач распознавания (этот класс получил короткое название NP (от слов Nondeterministic Polynomial)).

Итак, Выполнимость универсальна в NP. Однако, не смотря на более чем 100 летние усилия, не удалось найти для задачи Выполнимость эффективного детерминированного решающего алгоритма. Такая ситуация оказалась неслучайной. Сложность этой задачи оказывается большей, чем «пропускная способность» любого алгоритма, который был бы эффективным или детерминированным.

Остановимся на понятии пропускной способности канала связи, которые легко применить к вычислительной машине, решающей задачи.

Под пропускной способностью канала связи понимают величину

,

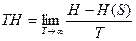(10.2)

где H – энтропия системы до передачи сообщения;

H(S) – энтропия системы после передачи сообщения S;

T – время передачи.

Проще говоря, TH определяет, какое максимальное число бит информации в единицу времени может быть передано через канал связи. Очевидным образом следует признать, что эта величина имеет предел в силу конечности скорости света (во всяком случае, нам не известны в природе взаимодействия, протекающие с большей скоростью).

Количество информации, содержащейся в системе дизъюнктов

Пусть A и B два дизъюнкта. В силу законов теории вероятностей можно записать

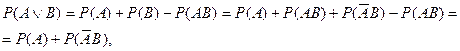
(10.3)

Здесь P(А) – вероятность того, что произвольная интерпретация I выполняет формулу A.

Далее, если 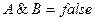(ложь), то

,

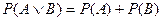(10.4)

Обобщением (8.3) для произвольного числа формул (дизъюнктов) служит

.

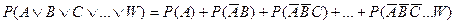(10.5)

Наконец, заметим, что вероятность выполнения формулы

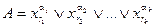
есть

,

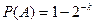(10.6)

А вероятность выполнения формулы

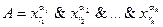
есть

.

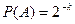(10.7)

Пример. Пусть дана формула 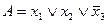. Тогда, в силу (8.6), вероятность ее выполнения суть

.

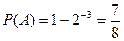Теорема .Пусть даны две формулы A и B и пусть 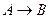(B следует из A). Тогда

.

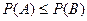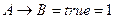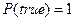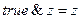Доказательство. По условию, . и для любой формулы z. Тогда, учтя, что 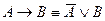, получим

.

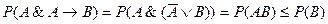Но 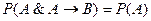, так как 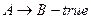. Поэтому .

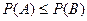Определение.Энтропией формулы A с n переменными называется величина

.

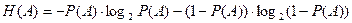(10.8)

При решении задач, связанных с угадыванием ответа, а задачи распознавания свойств относятся к таковым, естественно считать, что если 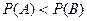, то задача A сложнее задачи B, поскольку в случае задачи A придется сделать большее число проб, чтобы угадать решение. В то же время не всегда имеет место соотношение

,

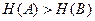когда

.

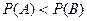Например, , .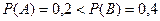

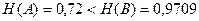Таким образом, энтропия, стандартным образом определяется по формуле (10.8), не отражает сложность задачи угадывания (энтропия больше, а перебора меньше). Это говорит о необходимости иного подхода к оценке сложности решения задач типа Выполнимость.

При решении задач решатель работает с условиями задачи. Часть условий задана явным образом, часть скрыта в ее содержании.

Условие «принимается» во внимание, если решатель затрагивает один или более тактов своей работы на проверку истинности (ложности) условия.

Условие, логически не следующее из других условий, называется независимым (от этих последних).

Для данного множества условий 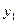, , 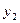…, 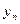условие 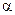является простейшим, если его по форме можно представить как дизъюнкт, никакой собственный поддизъюнкт которого не содержится среди дизъюнктов формулы логически эквивалентной .

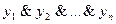Пример. Рассмотрим формулу 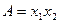. Ей эквивалентна формула 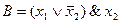. Дизъюнкт 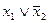не является простейшим, так как его поддизъюнктом является 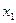, входящий в эквивалентную формулу 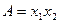, состоящую из дизъюнктов 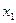и .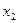

Минимально необходимое и достаточное число простейших независимых условий 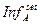, записанных с помощью переменных задачи A, которое должен принять во внимание решатель этой задачи, называется инфологической сложностью задачи A, а элементы 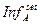– инфами.

Мы рассматриваем только алгоритмы, принимающие инфы во внимание, т.е. не игнорирующие инфы, так как при игнорировании инфа условие не берется в расчет, как если бы его не было, что нелепо, ибо инф есть необходимое и независимое от других условие. Игнорирование инфов наделяет алгоритм качеством оракула, что нами не допускается.

Алгоритм, не игнорирующий инфы, назовем «реалистическим». Не оговаривается, впрочем, как алгоритм получает инф и как он представлен.

Условие, эквивалентное множеству не менее двух инфов, называется формой. Принять форму во внимание – значит заменить индивидуальный анализ инфов задачи распознаванием истинности некоторого предиката (условия срабатывания формы), который определяется способом записи (спецификации) задачи. Очевидным образом предполагается, что между формальным представлением задачи (спецификацией) и ее содержанием (множеством инфов) существует связь.

Рассматриваем только такие задачи, которые формулируются в терминах 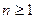однородных булевых переменных 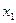, , 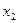…, 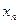и решением (выполняющим набором, интерпретацией) является множество индивидуальных значений для переменных 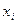( 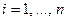), удовлетворяющих условиям задачи, представленным в ее спецификации. Это отличает такого рода задачи от «ДА-НЕТ»-задач, хотя и не принципиально. Кроме того, в качестве решения принимается любой подходящий набор из числа выполняющих. В силу теорему С. Кука будем иметь дело только с задачами Выполнимость, если противное не оговорено явно. Таким образом, слово «задача» понимается как «задача Выполнимость».

В последующем изложении будем использовать следующие предположения.

Во-первых, никакой реалистический алгоритм не использует никаких иных способов работы с инфами, кроме как выполняя индивидуальный анализ инфов и/или анализ форм. Во-вторых, для реалистических алгоритмов исключена возможность игнорировать инфы.

Подведем краткий итог. Мы показали, что энтропия не всегда правильно предает сложность задачи. Поэтому было введено понятие инфа и инфологической сложности. Далее мы представим некую теорию, которая объясняет, почему задача Выполнимость не имеет эффективных решающих алгоритмов.

ЛЕКЦИЯ 11. Постулаты теории инфологической сложности

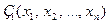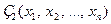Определение. Две задачи и записанные на одном и том же множестве переменных, эквиваленты, если выполняющие их наборы суть одно и тоже множество либо обе задачи не выполнимы.

Определение. Выполнимая задача B называется ослаблением выполнимой задачи A, если часть (пустую или нет) или все условия задачи A заменить их следствиями (хотя бы одним следствием).

Замечание. Замена пустой части условий следствиями означает присоединение следствий.

ПОСТУЛАТ 1.

1а. Инфологическая сложность любой задачи, сформулированной как задача отыскания произвольного выполняющего набора на множестве булевых переменных, есть целое неотрицательное число.

1b. Инфологическая сложность любой задачи A(x), формализованной на основе единственной переменной 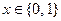, не выше 2.

1c. Всякая выполнимая ослабленная задача имеет инфологическую сложность, не превосходящую сложность исходной выполнимой задачи.

Замечание. Невыполнимая задача 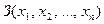в общем случаем может содержать невыполнимую часть в качестве собственного подмножества. Указать a priori, какова эта часть в общем случае, не решая задачу, нельзя. Однако невыполнимость этой части достаточна для того, чтобы игнорировать оставшуюся часть задачи и не принимать во внимание содержащиеся в ней инфы. Для выполнимых задач это невозможно ввиду того, что инфы представляет не зависимые от других простейшие условия.

Следствие. Любая выполнимая задача содержит число инфов не меньшее, чем любая ее ослабленная задача.

Обоснование п. 1с постулата 1 видеть можно в том, что в силу теоремы вероятность выполнимости ослабленной задачи не меньше вероятности выполнимости исходной задачи, а отбрасывание части дизъюнктов только увеличивает вероятность выполнимости оставшихся. Мы стоим на позиции, что чем больше вероятность выполнимости задачи, тем легче эта задача (менее сложна!).