ЛЕКЦИЯ 9. Метод резолюций Робинсона.

Напомним, что задача ВЫПОЛНИМОСТЬ требует установить, имеется ли для данной системы дизъюнктов общая выполняющая интерпретация. Напомним также, что примерами дизъюнктов являются следующие:

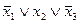
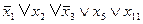
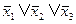
и т.д.

Здесь х_i являются булевскими переменными. Булевская переменная может принимать только два значения: 0, 1. Черта сверху над переменной означает ее отрицание. Правила отрицания таковы:

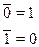
Значок v называется операцией логическое “ИЛИ” (а также дизъюнкцией). Эта операция дает в результате единицу, если и только если хотя бы одна из участвующих в ней переменных равна 1. Таким образом, дизъюнкт 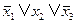равен 1 при значениях переменных, представленных в следующей таблице

Набор логических значений для переменных называется интерпретацией. Интерпретация, при которой дизъюнкт равен 1, называется выполняющейинтерпретацией.

Задача ВЫПОЛНИМОСТЬ заключается в следующем. Имеется множество дизъюнктов. Спрашивается, имеется ли для этого множества дизъюнктов хотя бы одна общая выполняющая интерпретация? Если ДА, то множество дизъюнктов называется выполнимым. Если НЕТ, то множество дизъюнктов называется невыполнимым. Эта задача имеет только кажущуюся простоту. На самом деле, проблема упирается в отыскание эффективного алгоритма ее решения, которую мы рассматриваем на следующем практическом занятии.

Принцип резолюций. Принцип резолюций заключается в систематическом построении следствий из текущей системы дизъюнктов на основе операции резолюционирования. Следствия называются резольвентами. Резольвенты строятся для пары дизъюнктов, содержащей контрарную пару литер (булевских переменных). Например, пусть даны два дизъюнкта

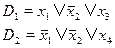
Эти дизъюнкты содержат контрарную пару литер - 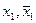(одна входит в дизъюнкт D₁ без отрицания, вторая – в дизъюнкт D₂ с отрицанием).

Резольвентой дизъюнктов D₁ и D₂ является новый дизъюнкт D_1,2 , который не содержит контрарной пары литер, но содержит все другие литеры из D₁ и D₂. Согласно этому определению, получим D_1,2= .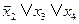

Целью построения резольвент является достижение следующих возможных исходов:

· Резольвента оказалась пустой. Например, пустую резольвенту дает следующая пара дизъюнктов

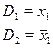
В случае пустой резольвенты делается вывод о невыполнимости системы дизъюнктов (т.е. задача ВЫПОЛНИМОСТЬ не имеет решения в этом случае).

· Невозможно построить новую резольвенту (началось зацикливание). В этом случае делается вывод о выполнимости исходной системы дизъюнктов.

Рассмотрим некоторый полный пример.

Решить следующую задачу ВЫПОЛНИМОСТЬ.

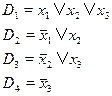
Находим резольвенту D₁ и D₂ :

D_1,2=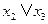

Находим резольвенту D_1,2 и D₃ :

D_1,2,3=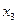

Дизъюнкты D_1,2,3 и D₄ дают пустую резольвенту. Вывод – исходная задача ВЫПОНИМОСТЬ не имеет решения.

Проблема метода резолюций – его неэффективность в сложностном смысле. Найти эффективный алгоритм для задачи ВЫПОЛНИМОСТЬ или доказать, что такого алгоритма нет – одна из глобальных нерешенных задач современности. Различные модификации принципа резолюций направлены на сокращение перебора.

Метод отсечения литер.

Рассмотрим одну из заслуживающих внимания модификаций принципа резолюций.

Этот метод заключается в последовательном исключении булевских переменных из системы. Сначала избавляемся, скажем, от переменной 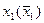, затем – от переменной 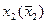и т.д. Такой систематический процесс рано или поздно завершится и по получению (не получению) пустого дизъюнкта можно будет судить о противоречивости системы (или нет). Рассмотрим пример из задания 1. Для начала избавимся от переменной 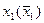. С этой целью выпишем все дизъюнкты, содержащие переменную :

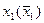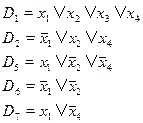
Теперь найдем все возможные резольвенты выписанных дизъюнктов с исключаемой литерой 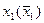. Выпишем эти резольвенты отдельно и добавим к ним те дизъюнкты из исходной системы, которые не содержали литеры 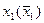. Получим следующую систему:

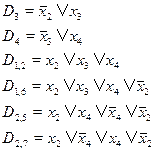
И эту систему можно еще более упростить, если удалить как бесполезные так называемые тавтологические дизъюнкты. Дизъюнкт называется тавтологическим, если он содержит как переменную, так и ее отрицание. В итоге, последняя система упрощается до следующей

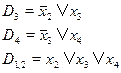
Продолжаем процесс избавления от переменных. На этот раз исключим переменную

Получим следующую систему

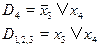
Теперь ясно, что никакого пустого дизъюнкта получить не удастся. Делаем вывод, что система выполнима (не противоречива).