ИЗМЕРЕНИЕ МОДУЛЯ ЮНГА

Измерительная установка (рис.1.9.2) состоит из звукового генератора (ЗГ), трех стержней из стали, бронзы и алюминия, закрепленных посередине, электромагнитного возбудителя колебаний (телефон Т), приемника (микрофон М), сигнал которого подается на вход осциллографа (ОСЦ). Переменное напряжение от звукового генератора подводится к телефону, вследствие чего на один из торцов стержня действует периодически изменяющаяся сила. В стержне возбуждается продольные волны. К другому торцу стержня подведен электромагнитный приемник, преобразующий звуковые колебания в электрические. Сигнал с приемника подается на вход усилителя осциллографа, длинна полоски на экране которого пропорциональна амплитуде колебаний конца стержня. Плавно изменяя частоту звукового генератора, при некотором ее значении 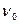обнаруживаем резкое возрастание амплитуды колебаний. Стержни начинают при этом звучать, а длина полоски на экране становится максимальной, т.е. наблюдается описанный выше резонанс, обусловленный возникновением в стержне стоячей звуковой волны с пучностями на обоих его торцах. Наблюдая это явление мы можем установить основную собственную частоту колебаний стержня 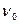и по формуле (12) вычислить, измерив длину стержня l, скорость распространения в нем продольной волны

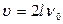(15)

При распространении в упругой твердой среде плоской продольной волны среда деформируется (растягивается или сжимается) в направлении распространения. Поэтому скорость волны должна зависеть от величины, характеризующей упругие свойства среды при ее растяжении или сжатии. Такой величиной является модуль Юнга, смысл которого устанавливается законом Гука, утверждающим, что абсолютное удлинение (укорочение) 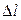циллиндрического однородного стержня в упругой стадии деформации прямо пропорционально растягивающей (сжимающей, силе F, т.е. 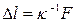, или для компенсирующей F силы упругости

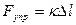. (16)

Коэффициент пропорциональности

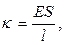(17)

где Е – модуль Юнга, зависящей только от материала стержня и являющейся характеристикой его упругих свойств, S и l – соответственно площадь поперечного сечения и длина недеформированного стержня.

Найдем связь между скоростью распространения упругой продольной волны в среде и ее модулем Юнга.

В стержне, в котором установилось стоячая волна, все его частицы совершают гармонические колебания, одновременно проходя положения равновесия и одновременно достигая крайних точек. При этом их полная механическая энергия остается постоянной во времени.

Вычислим полную механическую энергию колеблющихся частиц в стоячей волне с определяемой формулой (15) частотой основного тона ,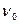

Из (13) с учетом (12) следует, что уравнение этой волны имеет вид

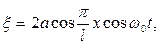(18)

где

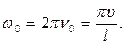(19)

Выделим теперь в стержне элементарный цилиндр, объемом 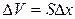, заключенный между его сечениями с координатами х и 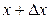(рис. 1.9.3), столь малый, что все его частицы имеют в рассматриваемый момент времени t приблизительно одинаковую скорость, проекция которой на ось х равна 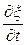, а относительное удлинение 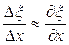(это равенство тем точнее, чем меньше 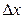). Здесь 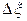- удлинение элементарного цилиндра, обусловленное смещением его частиц относительно положений равновесия к моменту времени t.

Тогда кинетическая энергия частиц этого цилиндра

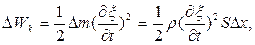(20)

где 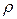- плотность материала стержня, невозмущенного волновым процессом, а потенциальная энергия их взаимодействия

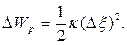(21)

Учитывая, что, согласно (17), 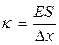, формула (21) перепишется так

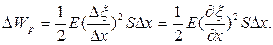(22)

Таким образом, полная механическая энергия частиц выделенного цилиндра

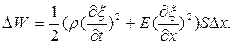(23)

Тогда полная механическая энергия частиц стержня, в котором установилась стоячая волна (18), определяется интегралом

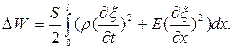(24)

Подставляя в (24) следующие из (18) и (19) выражения для производных

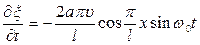
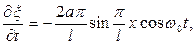
и учитывая, что

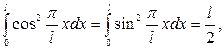
получаем

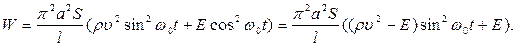(25)

Из (25) очевидно следует, что W=const только при выполнении равенства

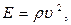
(26)

откуда

.

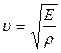Таким образом, скорость распространения продольной волны в упругой среде определяется как ее плотностью 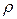, так и характеристикой ее упругих свойств – модулем Юнга Е. Формула (26) является теоретическим основанием для измерения модуля Юнга методом стоячих волн (его называют также методом измерения модуля Юнга в динамическом режиме). Действительно, подставляя (15) в (26) получим формулу для косвенного измерения модуля Юнга

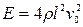(27)

Литература

1. Савельев И.В. Курс общей физики - М. Наука, 1988. т.2. - § 93 – 101.