Измерение момента инерции и модуля сдвига

Момент инерции твердого тела в ряде случаев можно легко рассчитать теоретически. В частности, момент инерции однородного диска (цилиндра), используемого в работе в качестве эталонного тела, относительно оси симметрии Z (рис.1.4.3) задается формулой

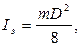(11)

где m и D – соответственно масса и диаметр диска.

Подвешивая на одной и той же проволоке эталонное тело с известным 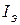, а затем тело с неизвестным моментом инерции I, можно экспериментально определить промежутки времен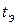и и 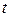, в течение которых совершаются 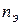и 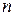колебаний эталонным телом и телом с неизвестным моментом инерции. Тогда в соответствии с (10)

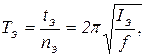(12)

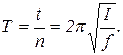(13)

Разделив почленно (13) на (12) , после возведения полученного равенства в квадрат находим

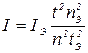(14)

В процессе проведения эксперимента целесообразно выбрать 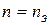. Тогда с учетом (11) для неизвестного момента инерции получаем следующую расчетную формулу

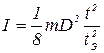(15)

Для измерения модуля сдвига материала проволоки используется только эталонное тело. В этом случае из (11) и (12) с учетом (2) получаем

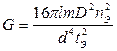(16)

Литература

1 .Савельев И.В. Курс общей физики - М. Наука, 1988. т.1. - §§ 13,26,28-33.

2. Савельев И.В. Курс общей физики - М. Наука, 1989. т.1. - §§ 38,39,41,43,53.

ИЗМЕРЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА И СИЛЫ ТРЕНИЯ В ОПОРЕ

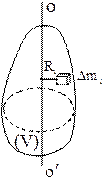Моментом инерции твердого тела относительно некоторой оси оо¢ (рис.1.5) называют величину 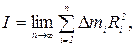(1) где 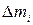- масса i – й материальной точки, на которые на которые мысленно разбито тело 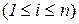, R_i - ее расстояние до выбранной оси. Если масса 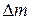сосредоточена в элементарном объеме 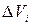, а плотность вещества в окрестности рассматриваемой точки тела

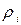, то 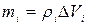и вместо (1) можно записать

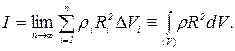(2)

Предлагаемый метод экспериментального определения момента инерции твердого тела основан на изменения механической энергии системы в процессе изучаемого движения (см. лаб.работу 1.2.).

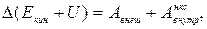(3)

где 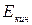- кинетическая энергия системы, 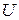- ее собственная потенциальная энергия, 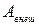- суммарная работа всех внешних сил, действующих на систему, 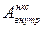- суммарная работа всех внутренних неконсервативных сил.

Если среди внешних сил имеются как консервативные, так и не-консервативные, то суммарная работа консервативных сил, если она не равна тождественно нулю, может быть представлена как убыль некоторой функции координат материальных точек системы 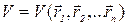, называемой потенциальной энергией системы во внешнем силовом поле. Например, система n – материальных точек, находящихся вне однородного шара массы М , обладает в его гравитационном поле потенциальной энергией вида

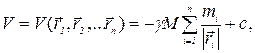(4)

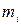где и 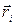- соответственно масса i – й материальной точки и ее радиус - вектор, проведенный из центра шара, С - произвольная постоянная. С помощью выражения (4) легко показать, что в пределах небольших высот потенциальная энергия тела массы 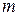поверхности Земли равна

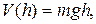(5)

где g - ускорение свободного падения у поверхности Земли, h – высота центра инерции тела над произвольно выбранным у поверхности Земли нулевым уровнем потенциальной энергии (это достигается фиксацией в (4) численного значения константы С).

Представляя теперь 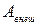в виде

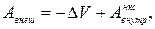(6)

где - 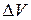- убыль потенциальной энергии системы во внешнем поле, 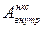-суммарная работа внешних неконсервативных сил, вместо (3) получаем

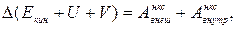(7)

величину

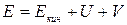(8)

называют полной механической энергией системы во внешнем поле.

Предлагаемый в данной работе метод определения момента инерции махового колеса основан на использовании закона изменения полной механической энергии системы в поле силы тяжести. В рассматриваемом случае на систему груз + маховик действуют внешние консервативные силы тяжести и реакции опоры, а также неконсервативные силы сопротивления воздуха и трения в опорных стойках махового колеса. Пренебрегая работой силы сопротивления воздуха и работой внутренних неконсервативных сил, пользуясь уравнением (7), запишем

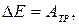(9)

где 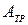- работа силы трения в опоре.

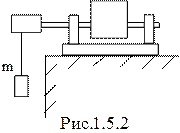
Пусть в начальный момент времени 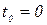подвешенный груз массой m (рис.1.5.2) Находится на высоте h (от наиболее низкого положе­ния, до которого может опустится груз. (рис.1.5.2). Тогда, учитывая возможность произвольного выбора нулевого уровня потенциальной энергии, начальная энергия рассматриваемой системы, в пренебрежении массой нити, будет равна

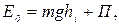(10)

где П – сумма потенциальной энергии махового колеса со шкивом в поле силы тяжести и собственной потенциальной энергии системы. Считая, что изменение последней в. процессе движения пренебрежимо мало, в нижней точке для полной энергии получаем

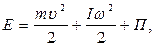(11)

где 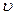- скорость подвешенного тела в нижней точке, 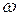- угловая скорость вращения шкива в соответствующий момент времени, 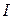- момент инерции махового колеса относительно оси вращения. Тогда согласно (9),

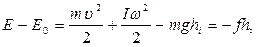(12)

где f – сила трения в опоре (предполагается, что в процессе движения f=const).

Силу трения можно вычислить, снова используя уравнение (9). Вращаясь по инерции, маховое колесо поднимает груз на высоту h₂<h₁. При этом согласно (9),

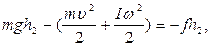(13)

Складывая (12) и (13), получаем

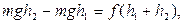(14)

Откуда

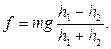(15)

Так как, по предположению, движение груза равноускоренное, то в нижней точке

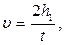(16)

где t – время опускания груза. Поскольку нить сматывается со шкива без проскальзывания, то для угловой скорости в момент t имеем

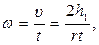(17)

где r - радиус шкива.

Представляя (15) - (17) в уравнение (12), после преобразований получаем искомую формулу для момента инерции:

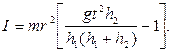(18)

Литература

1. Савельев И.В. Курс общей физики. Т.1. – М.: Наука, 1989, §§ 19-22,38,39,41,45,46.