ИЗМЕРЕНИЕ МОДУЛЯ ЮНГА МЕТОДОМ СТОЯЧИХ ВОЛН В СТЕРЖНЕ

Процесс распространения колебаний в пространстве называется волной. Волны, возникающие в упругой среде (твердой, жидкой или газообразной), называются упругими волнами. При распространении упругой волны частицы среды не вовлекаются в поступательное движение, а только совершают колебания около своих положений равновесия. Уравнением волны называют функцию 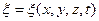, определяющую смещение частицы среды из положения равновесия с координатами 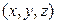, в момент времени t. В случае, если направление колебаний частиц среды совпадает с направлением распространения волны, волны называются продольными, если направление колебаний частиц перпендикулярно направлению распространения волны – поперечные.

Геометрическое место точек, до которых доходит волна к моменту времени t, называется волновым фронтом. В случае, если волновой фронт имеет форму плоскости волна называется плоской, сферы – сферической.

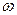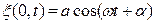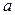Получим уравнение плоской волны, распространяющей вдоль оси х. Предположим, что ее источник находится в начале координат и совершает гармонические колебания с частотой по закону , где и 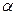, соответственно амплитуда и начальная фаза колебаний.

При распространении колебаний от источника вдоль оси х отклонение 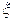частицы среды от положения равновесия с координатой х определяется уравнением

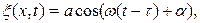(1)

где 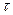- время, в течение которого колебания от источника дойдут до точки среды с координатой х.

Если 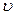- скорость распространения колебаний (волны), то 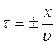, где знак “+” отвечает волне, распространяющейся в положительном направлении оси х, а знак “-” – в отрицательном. Тогда, принимая во внимание , что

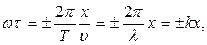
где Т – период колебаний, 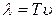- длина волны, 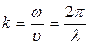- волновое число, перепишем (1) в виде

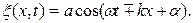(2)

Функция (2) и представляет собой искомое уравнение плоской волны, распространяющейся вдоль оси х, причем знак “-” соответствует волне, распространяющейся в положительном направлении оси х, знак “+” в отрицательном.

Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы среды при распространении каждой из волн в отдельности. Это справедливо для волн любой природы и получило название принципа суперпозиции. В случае, когда колебания, обусловленные отдельными волнами, в каждой точке среды обладают постоянной разностью фаз, такие волны называют когерентными. В случае наложения двух и более когерентных волн с одинаковыми направлениями колебаний частиц, наблюдается явление перераспределения колебаний в пространстве с образованием устойчивой картины чередования минимумов и максимумов амплитуд колебаний. Такое явление называется интерференцией.

При наложении двух когерентных плоских волн с одинаковыми амплитудами, направленными навстречу друг к другу, в результате их интерференции возникает колебательный процесс, называемый стоячей волной

Найдем уравнение плоской стоячей волны в однородном стержне длинной l, закрепленном в середине, а также спектр его собственных частот.

Пусть на торце стержня с координатой х=0 созданы гармонические колебания 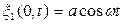(источник колебаний). Тогда вдоль стержня, лежащего на оси х (рис.1.9.1) будет распространятся упругая плоская волна

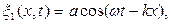(3)

которая затем отражается от свободного торца стержня с абсциссой х=l, так что в каждой точке волнового поля между торцами будет складываться колебания в падающей и отраженной волнах. Уравнение отраженной волны, распространяющейся от торца 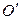противоположно направлению оси 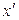, имеет вид

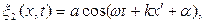(4)

где 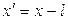, 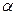- константа, значение которой должно обеспечивать условие закрепленности стержня в его середине.

Складывая уравнения (3) и (4) с учетом того, что 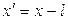, находим уравнение волнового процесса в стержне

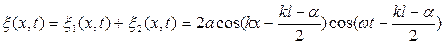(5)

Функция (5), также как (3) и (4), имеет смысл смещения частицы среды от ее равновесного положения с абсциссой х в момент времени t. Однако в отличие от волновых процессов, описываемых функциями (3) и (4), в которых каждая точка среды колеблется с одинаковой амплитудой 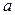, функция (5) описывает процесс в котором каждая частица среды колеблется с амплитудой, зависящей от координаты х:

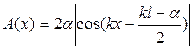(6)

Такой колебательный процесс частиц среды называют стоячей волной. Функцию (5) называют уравнением плоской стоячей волны.

Используя выражение (6), мы можем теперь выразить условие закрепленности стержня в его середине равенством

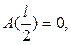(7)

означающим неподвижность частиц поперечного сечения стержня с абсциссой 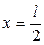. Тогда из (6) с учетом (7) вытекает, что

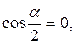
и, следовательно, для выполнения условия закрепленности стержня в его середине достаточно положить

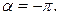(8)

Подберем теперь частоту колебаний источника так, чтобы отраженная волна вызывала в точке с абсциссой х=0, где расположен источник, колебания в фазе с ними, т.е.

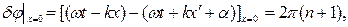(9)

где n=0,1,2,… . Учитывая (8) и то, что 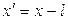, из (9) получаем

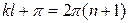(10)

Ясно, что при заданной длине стержня l, уравнение (10) выполняется лишь для определенного набора частот 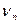, называемых собственными частотами стержня, закрепленного посередине. Учитывая, что 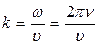из (10) получаем формулу для набора (спектра) собственных частот

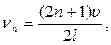n=0,1,2,3… (11)

Из (11) вытекает, что собственные частоты кратны частоте

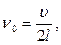(12)

называемой основной частотой. В акустике частоту 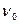называют также частотой основного тона, тогда как 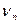, при 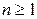, - частотами обертонов.

Легко видеть, что при выполнении равенств (8) и (10), приводящих к частоте (11), уравнения (5) и (16) перепишутся в простом виде

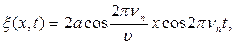(13)

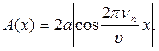(14)

Точки, в которых амплитуда стоячей волны А(х) обращается в нуль, называется узлами стоячей волны. Точки, колеблющиеся с максимальной амплитудой 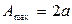, называются пучностями стоячей волны. Тогда из (14) с учетом (11) вытекает, что в середине стержня реализуется узел 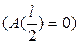, а на обоих торцах стержня – пучности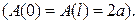

Таким образом, при совпадении частоты источника с любой из собственных частот стержня (11), амплитуда колебаний точек его торцов увеличивается в два раза по сравнению с амплитудой колебаний источника. Это явление по аналогии со случаем вынужденных колебаний называют резонансом.