Амплитудная модуляция

При амплитудной модуляций изменяется амплитуда высокочастотного несущего колебания (1.1) пропорционально u(t).

С учетом (1.2), вынося U₀ зa скобки, выражение (1.1) можно представить в следующем виде:

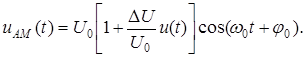(1.5)

Выражение (1.5) описывает амплитудно-модулированный (AM) сигнал. Если до модуляции амплитуда колебаний (1.1) была постоянна, то теперь она будет изменяться по закону низкочастотного первичного сигнала u(t). Поэтому сигнал u(t) называют модулирующей функцией. Она может быть непрерывной или дискретной. Для непрерывного сообщения функции u(t), f(t) и u_АМ приведены на рис. 1.12, а.

Для дискретного сообщения, если оно закодировано двоичным кодом, модулирующая функция u(t) будет принимать только два значения: 1 или 0. В этом случае амплитудную модуляцию называй амплитудной манипуля-цией (рис. 1.12, б).

Модуляция осуществляется в устройстве, называемом амплитудным модулятором. При подаче на один его вход напряжения несущей частоты, а на другой вход - низкочастотного первичного сигнала u(t), на выходе модулятора образуется амплитудно-модулированный или амплитудно-манипулированный сигнал.

Амплитудно-манипулированные сигналы чаще всего применяются в каналах слухового телеграфирования. Поэтому амплитудную манипуляцию называют амплитудным телеграфированием (AT). Режим AT относится к видам работы с пассивной паузой и обладает низкой помехоустойчивостью. В связи с этим его не применяют в каналах приема на автоматическую регистрирующую аппаратуру. В то же время режим AT весьма эффективен в слуховых каналах приема, использующих код Морзе. В силу физиологических особенностей слухового аппарата человека прием телеграфных сиг­налов оператором возможен даже в тех случаях, когда уровень сигнала соизмерим с уровнем помех или даже ниже его. Поэтому ре­жим AT применяется в самых современных системах связи.

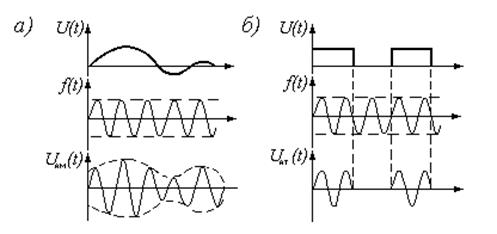
рис.1.12

Перейдем к рассмотрению спектра амплитудно-модулированного непрерывного сигнала. Для краткости в дальнейшем будем называть его спектром AM сигнала. Ранее уже отмечалось, что всякое колебание несинусоидальной формы имеет сложный спектр, поскольку содер­жит множество гармоник. Сигнал АМ является сигналом сложной фор­мы, что видно из рис.1.12,а. Для того чтобы разобраться, что же собой представляет спектр AM сигнала, максимально упростим за­дачу. Начнем с простейшего случая, когда модулирующая функция u(t) представляет собой косинусоидальное колебание низкой частоты , которое можно записать в виде .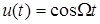

Подставляя это выражение в (1.5) и полагая начальную фазу 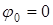, получим следующую формулу для AM сигнала.

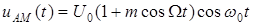, (1.6)

где 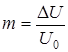- коэффициент глубины модуляции;

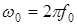- частота несущей;

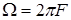- частота модулирующего сигнала u(t) ,

Для непрерывных сигналов выбирают 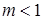, чтобы исключить специфические искажения - перемодуляцию. На практике величина 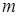=0,3-0,5. В случае же дискретных сигналов при передаче посылки (1) величина 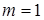, а при передаче паузы (0) величина 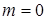. Но здесь модулирующая функция u(t) будет более сложной, а не синусоидальной.

Вернемся к случаю, когда 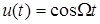. После соот­ветствующих перемножений формула (1.6) преобразуется к следующему виду:

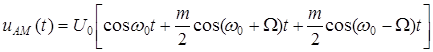. (1.7)

Из этой формулы видно, что такой AM сигнал содержит три составляющих: колебание несущей частоты 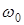и две боковые частоты: 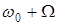и 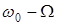. Это и есть спектр AM сигнала (рис.1.13,а).

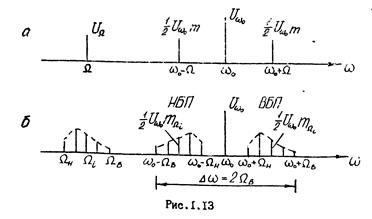
Амплитуды боковых частот одинаковы и пропорциональны коэф­фициенту глубины модуляции m .

Мощность AM сигнала зависит от величины m . При этом мощ­ность несущей частоты, равная 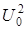, неизменна, а мощность каж­дой боковой частоты равна .

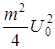Интересно отметить, что боковые частоты 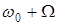и 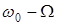представляют собой зеркальное отображение друг друга по отноше­нию к несущей частоте 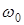. Они несут одну и ту же информацию о передаваемом сигнале. Несущая же частота вообще не несет никакой информации, хотя и потребляет 50 ⁰/₀ мощности. То, что именно боковые составляющие несут информацию , подтверждает следующий факт. При отсутствии модулирующего сигнала m=0 и боковые со­ставляющие 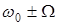исчезают, а остается только колебание несу­щей частоты 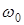. 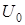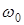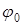Это и есть исходный материальный носитель, у которого параметры , и постоянны, а значит, не несут никакой информации. Этот принцип сохраняется и для тек слу­чаев, когда модулирующая функция 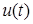имеет любую форму. При рассмотрении непрерывных сигналов было установлено, что речевой сигнал представляет собой сложную модулирующую функцию. Это видно из начертания фонем и спектрального состава формант. Даже при ограничении полосы спектра речи рамками канала ТЧ, модулирующая функция 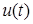будет содержать множество колебаний с частотами от 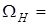300 Гц до 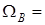3400 Гц ( 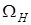и 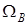- соответственно нижняя и верхняя частота канала ТЧ). Даже не производя математи­ческих выкладок, можно увидеть, что, подставляя в формулу (1.5) модулирующую функцию 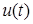, содержащую множество колебаний в диа­пазоне частот от 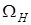до 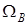, в результате будет получено то же самое колебание несущей частоты 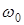и две боковые полосы частот вида 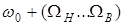и . 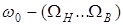Колебания 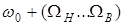называют верх-ней боковой полосой, а колебания 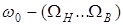- нижней боковой поло-сой. Таким образом, спектр непрерывного AM сигнала в общем случае состоит из двух боковых голос, несущих одну и ту же информацию, которые располо­жены симметрично по отношению к несущей 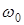(рис.1З,б).

Из рис.1.13,б видно, что полоса, занимаемая спектром непре­рывного AM сигнала, равна 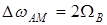. Такой сигнал имеет ряд недостатков. Во-первых, в энергетическом отношении он нераци­онален, так как половина мощности здесь тратится на несущую, а оставшаяся мощность делится пополам между информационными боковыми полосами. Следовательно, мощность передатчика используется крайне неэффективно. Во-вторых, для передачи такого сигнала полосу пропускания канала связи нужно иметь в два раза больше по сравнению с необходимой полосой для передачи низкочас-тотного первичного сигнала, в рассматриваемом случае речевого сигнала. В-третьих, при передаче AM сигнала по каналу связи с переменными параметрами в случае замирания несущего колебания 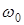может произойти полное нарушение связи.

Перечисленные недостатки резко ограничили применение этого вида модуляции в системах связи. Однако, именно амплитудная модуляция породила балансную и однополосную модуляцию.

Балансная модуляция (БМ) отличается отAM отсутствием несущего колебания 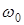. В этом случае вся мощ­ность передатчика делится поровну между верхней и нижней информационными полосами, что существенно повышает помехоустойчивость связи.

При однополосной модуляции (ОМ) по­давляется несущая и одна боковая полоса. Это позволяет весьма экономно использовать отводимую для связи полосу частот, так как ширина спектра однополосного сигнала (ВБП или НБП) равна ширине спектра модулирующей функции 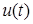, т.е. речевого сигнала. Теперь вся мощность передатчика тратится только на полезный сигнал. Кроме того, однополосный сигнал более устойчив к замираниям, так как в нем отсутствует несущее колебание с частотой 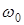. Все это дает возможность в существенной мере улучшить такие показатели системы связи, как помехоустойчивость и достоверность передачи. Вот почему однополосные сигналы находят самое широкое применение в системах проводной и радиосвязи.

Теперь перейдем к рассмотрению вопроса о спектрах дискрет­ных амплитудно-манипулированных сигналов или сигналов амплитуд­ного телеграфирования (AT). При AT возможна работа незатухающими и тональ-ными колебаниями. Случай AT незатухающими колебаниями показан на рис.1.12,б. Остановимся только на этом режиме работы поскольку он является основным в дискретных системах связи. В 1.1.2 при рассмотрении последовательности импульсов (рис.1.8,а) было показано, что их спектр состоит из нечетных гармонических составляющих F_М, 3 F_М, 5 F_М и т.д. Сигнал же амплитудной телеграфии - это высокочастотное колебание с частотой 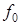. Поскольку амплитудная манипуляция есть процесс перемножения ко­лебаний 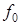и F_М, 3 F_М, 5 F_М и т.д., то результирующий сигнал будет представлять собой несущее колебание 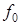и ряд боковых составляющих вида 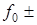F_М, 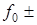3F_М и т.д., интенсивность которых быстро убывает с ростом их порядкового номера. На прак­тике полосу спектра сигнала AT ограничивают, исходя из соотно­шения 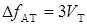, где 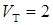F_М - скорость телеграфиро­вания. Этой полосы вполне достаточно, чтобы восстановить на при­емной стороне передаваемое дискретное сообщение.

Частотная модуляция

При частотной модуляции (ЧМ) изменяется частота высокочас­тотного несущего колебания (1.1) пропорционально 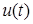. Особен­ностью частотной модуляций является то, что амплитуда этого ко­лебания остается неизменной во времени. Поэтому формулу для вы­сокочастотного колебания (1.1) с постоянной амплитудой, но пере­менной частотой теперь можно представить следующим выражением:

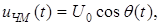(1.8)

где 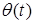- мгновенная фаза.

Дело в том, что фаза и частота колебания взаимосвязаны меж­ду собой . Для синусоидального колебания 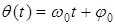, т.е. фаза растет пропорционально времени. Если колебание пред­ставить вектором, то это значит, что он вращается равномерно с постоянной угловой скоростью 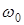. В случае же несинусоидально­го колебания частота непостоянна и вектор вращается с перемен­ной скоростью 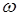. Мгновенное значение частоты определяется как производная по времени от фазы, т.е. 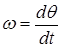. Из этого выраже­ния можно найти переменную фазу колебания. Она равна 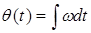. .Если подставить это выражение в формулу (1.8), то получим 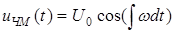. Здесь 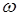определя­ется выражением (1.3). Подставляя значение 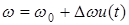под знак интеграла, получим

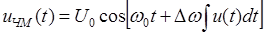, (1.9)

где 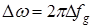- частотное отклонение от 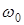или девиация частоты.

Выражение (1.9) описывает частотно-модулированный (ЧМ) сиг­нал. Если до модуляции частота колебания (1.1) была постоянна, то теперь она будет изменяться по закону низкочастотного первичного сигнала или, что то же самое, модулирующей функции 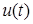. Она может быть как непрерывной, так и дискретной.

Для непрерывного сообщения функци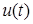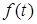и , и 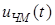приведенына рис.1.14, а.

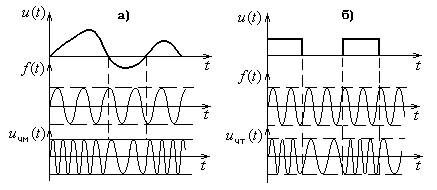
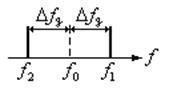
рис.1.14 рис.1.15

Для дискретного сообщения, закодированного двоичным кодом, модулирующая функция 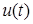будет равна либо 1, либо 0. В этом случае частотную модуляцию называют частотной манипуляцией (рис.1,14,б).

Модуляция несущей частоты производится в устройстве, которое называется частотным модулятором. В состав частотного моду­лятора входят контур, параметры, а значит, и частота которого ме­няются под воздействием модулирующего сигнала.

ЧМ сигналы находят широкое применение в каналах телеграфирования, поэтому частотную манипуляцию называют частотным телеграфирова-нием (ЧТ). Режим ЧТ относится к видам работы с активной паузой и обладает повышенной помехоустойчивостью по отношению к AT.

Остановимся несколько подробней на рассмотрение частотного телегравирования, поскольку оно находит широкое применение в различных системах проводной и радиосвязи.

Принцип ЧТ состоит в том, что при передаче токовой посылки передает-ся колебание с частотой 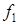, а при передачи бестоковой посылки - колебание с частотой 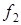. Согласно рекомендациям МККТТ принято, что 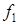> 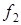[5].

В зависимости от вида кода различают:

- простые системы ЧТ, в которых применяется двоичный час­тотный код (m =2);

- система двойного частотного телеграфирования (ДЧТ) с ос­нованием частотного кода m= 4;

- системы многопозиционного частотного телеграфирования (МЧТ) с основанием частотного кода m > 2.

Отсюда следует, что ДЧТ является частным случаем МЧТ. На практике наибольшее распространение получили системы связи ЧТ и ДЧТ.

Основными параметрами сигнала ЧТ (рис. 1. 15) являются:

1. Среднее значе­ние частоты, вокруг которой осуществляется манипуляция частот токовой посылки 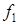и бестоковой посылки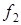

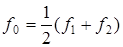. (1.10)

2. Разнос частот токовой и бестоковой посылки

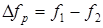. (1.11)

3. Девиация частоты, характеризующая отклонение частоты от ее среднего значения

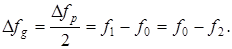(1.12)

4. Индекс частотной манипуляции

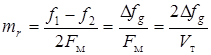, (1.13)

где 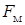- частота манипуляции сигнала, Гц;

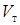- скорость телеграфирования, Бод.

Скорость передачи (телеграфирования) определяет основную частоту манипуляции или частоту следования импульсов (рис.1.8,а) и связана с ней соотношением

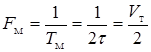. (1.14)

Рассмотрим теперь принцип ДЧТ. Он состоит в том, что один передатчик одновременно передает две различные информации двум корреспондентам. Для этого используют четыре различных частоты.

Если передачу посылки от телеграфного аппарата обозначит (+), а паузу - (-), то при одновременной работе двух аппаратов можно осуществись следующую группировку сигналов с точки зрения передачи в канал связи одной из частот:

1 канал	+	-	+	-
2 канал	-	+	+	-
Формируемые сигналы

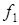
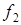
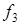
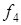
Отсюда следует, что одновременная двухканальная работа при ДЧТ достигается путем передачи в канал связи колебания только одной частоты, на которую расходуется вся мощность передатчика.

При независимой работе двух телеграфных аппаратов в канале связи вместо одной частоты нужно передавать одновременно две частоты. В этом случае мощность передатчика делится пополам между передаваемыми сигналами, что ведет к ухудшению такого показателя системы связи, как ее помехоустойчивость,

Нa рис. 1.16 показан сигнал ДЧТ. Из рисунка видно, что при ДЧТ индекс частотной манипуляции в три раза больше, чем при ЧТ.

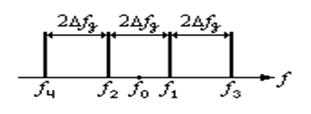
рис.1.16

Вернемся теперь к рассмотрению спектров ЧМ сигналов. Для непрерывного сигнала опять возьмем простейший случай, когда модулирующая функция 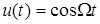. Тогда формула (1.9) преобразуется к виду

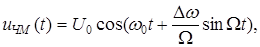(1.15)

где ;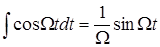

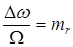- индекс частотной модуляции.

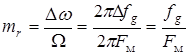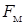Выражение для индекса частотной модуляции совпадает с фор­мулой (1.13). Действительно, , где - частота модуляции (манипуляции).

Вычисление выражения (1.15) показывает, что теоретически спектр ЧМ сигнала бесконечен и состоит из колебаний вида 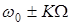, где K = I, 2, 3 ... Практически же ширину этого спектра можно ограничите, так как с ростом К амплитуда колебаний быстро убыва­ет. Установлено [2,5], что полоса спектра ЧМ сигнала в общем слу­чае зависит как от девиации частоты 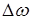, так и от значения мо­дулирующей частоты 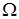. Другими словами, ширина спектра зависит от величины 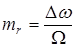. При индексах частотной модуляции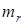 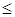1 ширина спектра ЧМ сигнала такая же, как у AM сигнала, т.е. равна удвоенной частоте модуляции. Однако, с ростом величины m_r ширина спектра ЧМ сигнала начинает возрастать и при 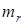>> 1 она равна 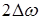, т.е. удвоенной девиации частоты. В процессе мо­дуляции мгновенная частота может принимать любое значение внутри интервала 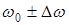. Следует отметить, что величина 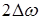учи­тывает обе боковые полосы ЧМ сигнала, каждая из которых при боль­ших значениях 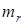равна 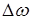. Сама же величина 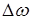выбирается по нашему усмотрению при проектировании системы связи и является не­которой постоянной.

Перейдем к рассмотрению спектра ЧМ дискретного сигнала. В 1.3 было показано, что даже при передаче простой последовательности импульсов, спектр сигнала состоит из ряда нечетных гармоник 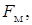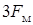, 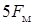и т.д., кратных основной частоте мани­пуляции .

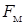Для того, чтобы найти спектр сигнала ЧТ, нужно в формулу (1.9) подставить аналитическое выражение, описывающее импульс­ный модули-рующий сигнал. Опуская математические выкладки, отме­тим, что спектр такого сигнала состоит из несущей частоты и бес­конечного числа частотных составляющих нижней и верхней боковых полос. Амплитуда частотных составляющих и ширина спектра главным образом определяются величиной индекса частотной манипуляции 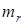и номером гармоники модулирующего сигнала.

При 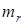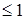спектры сигналов AT и ЧТ почти не отличаются. С ростом величины 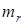спектр сигнала ЧТ начинает расширяться.

На практике ширину спектра сигнала ЧТ рассчитывают по формуле

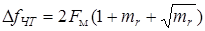. (1.16)

Для любого вида ЧМ сигналов помехоустойчивость связи повышается с ростом величины 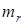, а это ведет к расширению спектра сигнала. Поэтому частотную модуляцию применяют, как правило, в широкополосных каналах связи.

Фазовая модуляция

При фазовой модуляции (ФМ) под действием модулирующего сигнала 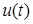изменяется фаза несущего колебания (1.1), а его амплитуда остается постоянной. Для ФМ сигнала формула (1.1), с учетом (1.4) преобразуется к виду

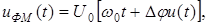(1.17)

где 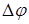- индекс фазовой девиации.

В формуле (1.17) начальная фаза 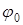отброшена, таккакона является пос-тоянной величиной. Как видно из формулы, модулирующая функция 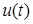здесь входит под знак косинуса. Выражение (1.17) для ФМ сигнала и (1.9) для ЧМ сигнала отличаются только тем, что в первом случае под знаком косинуса находится сама модулирующая функция, а во втором случае - ее интеграл.

Для непрерывного ФМ сигнала ширина боковой полосы, по аналогии с ЧМ сигналом, находится как произведение индекса фазовой девиации на модулирующую частоту, т.е. , а полная ширина спектра равна . Если для ЧМ сигнала ширина спектра не зависела от значения , то для ФМ сигнала она зависит от него. В этом и состоит различие спектров ФМ и ЧМ сигналов.

Фазовая модуляция не нашла практического применения для передачи непрерывных сообщений. Зато ее широко применяют при передаче дискретных сообщений.

При кодировании дискретных сообщений двоичным кодом (1,0) фазовую модуляцию называютфазовой манипуляцией. Поскольку фазовая манипу-ляция широко применяется в теле­графных и телекодовых каналах связи, она получила название фазового телеграфирования (ФТ),

Различают несколько способов фазового телеграфирования:

- однократное (ФТ);

- многократное (МФТ);

- относительное (ОФТ).

При ФТ фаза несущего колебания меняется скачком на 180° при переходе от посылки ( 1 ) к паузе ( 0 ), и наоборот (рис.1.17). Фазовую телеграфию называют режимом работы с активной паузой.

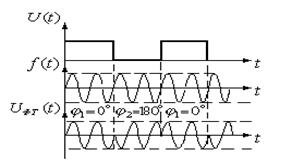
рис.1.17

Сигналы МФТ используются тогда, когда по каналусвязи пере­даются одновременно n сообщений. Частным случаем МФТ являетсядвойное фазовое телеграфирование (ДФТ). Здесь есть прямая анало­гия с сигналами двойного частотного телеграфирования (ДЧТ). Но там последовательно передавали одну из четырех частот ( 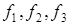или 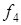), а при ДФТ передаются колебания одной и той же частоты, но с четырьмя различными фазам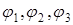и ( или 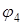). Если нужно передавать n сообщений, то понадо-бится сформировать коле­бания с n - фазами. Эти фазы находятся по формуле .

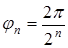В чистом виде сигналы ФТ не применяются из-за явления так называемой "обратной работы". Дело в том, что в отличие от сигна­лов AT и ЧТ прием сигналов ФТ требует подачи на демодулятор опор­ного напряжения синхронного и синфазного с принимаемом высокочас­тотным сигналом. Если произойдет случайный скачок фазы у сигнала или опорного напряжения, то все посылки станут паузами, а паузы - посылками. Это и есть явление “обратной работы”. Для того чтобы избежать этого недостатка, отечествен-ным ученым Н.Т. Петровичем был предложен способ относительного фазового телеграфирования (ОФТ). Он предусматривает опре­деленный алгоритм кодирования и декодированиясигналов, благода­ря чему явление обратной работы исключается. По своимосновным параметрам сигналы ОФТ ничем не отличаются от сигналов ФТ.

Принцип ОФТ заключается в сравнении фаз несущего колебания n – й и предыдущий (n –1)–й посылок. В результате носителем информации являет-ся не фаза принимаемой посылки, а новый сигнал, полученный по опреде-ленному правилу при сравнению фаз последующей и предыдущей посылок. Как правило, этот сигнал формируется до фазового манипулятора, поэтому сигналы на его выходе по виду ничем не отличаются от сигналов ФТ.

При ОФТ в случае передачи бестоковой посылки фаза ее колебаний остается такой же, как и предыдущей посылки, а при передачи токовой посылки изменяется на 180°. В принципе, это правило можно изменить на противоположенное. Но независимо от правила перекодирования в начале сеанса связи нужно передавать вспомогательный сигнал для определения фазы колебаний первой посылки.

Алгоритм перекодирования сигнала на передающей стороне можно записать в виде

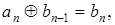(1.18)

где 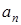- п-я посылка;

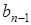- (n –1)-я посылка;

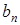- формируемая в результате перекодирования посылка.

Пользуясь (1.18), легко показать что исходная последовательность 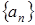=101101001 в результате перекодирования дает последовательность 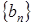=110110001. Эта операция иллюстрируется рис. 1.18. Технически перекодирование можно осуществить по схеме, приведенной на рис. 1.19. Посылки, поступающие на манипулятор фазы, одновременно задерживаются на время 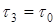в элементе задержки и подаются на сумматор по модулю два, где и происходит их перекодирование. В модуляторе фаза несущего колебания изменяется только при изменении полярности посылок.

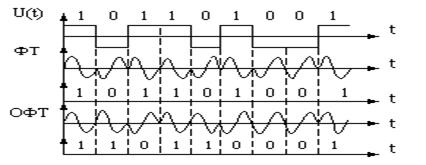
рис.1.18

На приемной стороне для восстановления исходного сообщения необходимо произвести операцию декодирования по формуле

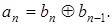(1.19)

Эту операцию можно реализовать, используя схему, приведенную на рис. 1.20.

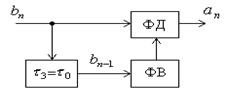
рис.1.19 рис.1.20 рис.1.21

Нетрудно показать, что принятая в этом случае последовательность 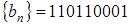будет преобразована в исходную последовательность 101101001.

На практике обработку принимаемого сигнала часто ведут не по низкой, а по высокой частоте. При этом посылки переменного тока поступают на входы фазового детектора и схемы задержки на время 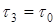, а с нее через фазовращатель ФВ – на другой вход ФД (рис. 1.21). В фазовом детекторе роль опорного напряжения для п-й посылки играет (п – 1)-я посылка. В результате сравнения последующей высокочастотной посылки с предыдущей формируется исходная кодовая комбинация.

Выбранные алгоритмы перекодирования и декодирования сигналов практически устраняют «обратную работу», характерную для ФТ. Изменение полярности посылок на входе сумматора по модулю два не изменяет полярности выходных сигналов, за исключением двух посылок, непосредст-венно примыкаемых к моменту скачка фазы.

Вид спектров сигнала ОФТ зависит от способа сравнения посылок на приемном конце, т.е. от того, каким способом обрабатывается принятый сигнал – путем сравнения полярностей или путем сравнения фаз. Способ сравнения фаз получил название ОФТ-1, а способ сравнения полярностей ОФТ-2. Что же касается ширины спектра сигналов ОФТ-1 и ОФТ-2, то они почти не отличаются от спектра сигналов ФТ.

При ОФТ, как при ФТ, возможна реализация многократного телеграфи-рования и, в частности, двукратного ОФТ (ДОФТ). Для этого необходимо на передающей стороне расщепить несущее колебание на два колебания со сдвигами фаз относительно исходного на 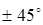. На приемном конце эти колебания анализируются по способу сравнения фаз (ДОФТ-1) или полярностей (ДОФТ-2).

Следует отметить, что в каналах относительного фазового телеграфирования нужно обеспечит высокую стабильность частоты колебаний, причем эти требования возрастают с повышением рабочей частоты и скорости телеграфирования.

В настоящее время методы относительного фазового телеграфирования находят все большее применение в ряде отечественных и зарубежных систем радиосвязи.

В отличие от сигналов ЧТ, где для передачи информации ис­пользуются колебания двух частот, сигналы ОФТ передаются колеба­нием только одной частоты, как при AT. Отсюда следует, что шири­на спектра сигналов ОФТ и AT совпадает. Различие состоит лишь в уровнях гармонии. У сигнала ОФТ амплитуды гармоник зависят от значения индекса фазовой девиации .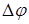

Спектр сигнала при многократном фазовом телеграфировании по ширине совпадает со спектром сигнала ОФТ. Вторым преимуществом сигналов фазовой телеграфии является работа с активной паузой, при которой лучше реализуется мощность сигнала. И, наконец, третьим преимуществом является то, что за счет когерентной обработки сигналов фазового телеграфирования на приемной стороне их уровень по сравнению с сигналами АТ возрастает в два раза, что эквивалентно увеличению отношения сигнал/помеха по мощности в четыре раза.

Узкополосность сигналов ОФТ и их хорошие энергетические показатели обеспечивают системам связи с относительным фазовым телеграфированием высокую помехоустойчивость, превышающую помехоустойчивость систем связи с ЧТ, а тем более, с АТ. Поэтому сигналы ОФТ считаются весьма перспективными.