Амплитудная модуляция

Амплитудная модуляция — вид модуляции, при которой изменяемым параметром несущего сигнала является его амплитуда

Определение

Пусть

§ S(t) — информационный сигнал, | S(t) | < 1,

§ U_c(t) — несущее колебание.

Тогда амплитудно-модулированный сигнал U_am(t) может быть записан следующим образом:

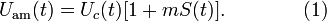
Здесь m — некоторая константа, называемая коэффициентом модуляции. Формула (1) описывает несущий сигнал U_c(t), модулированный по амплитуде сигналом S(t) с коэффициентом модуляции m. Предполагается также, что выполнены условия:

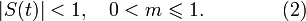
Выполнение условий (2) необходимо для того, чтобы выражение в квадратных скобках в (1) всегда было положительным. Если оно может принимать отрицательные значения в какой-то момент времени, то происходит так называемая перемодуляция (избыточная модуляция). Простые демодуляторы (типа квадратичного детектора) демодулируют такой сигнал с сильными искажениями.

Пример.

Допустим, что мы хотим промодулировать несущее колебание моногармоническим сигналом. Выражение для несущего колебания с частотой ω_c, начальную фазу положим равной нулю, имеет вид

U_c(t) = Csin(ω_ct).

Выражение для синусоидального сигнала с частотой ω_s(сигнал подлежащий передаче) имеет вид

U_s(t) = U₀sin(ω_st + φ),

где 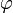— начальная фаза. Тогда, в соответствии с (1)

U_am(t) = C[1 + mU₀sin(ω_st + φ)]sin(ω_ct).

Приведённая выше формула для y(t) может быть записана в следующем виде:

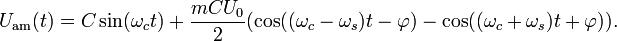
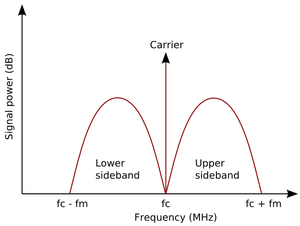
Радиосигнал состоит из несущего колебания и двух синусоидальных колебаний, называемых боковыми полосами, каждое из которых имеет частоту немного отличную от ω_c. Для синусоидального сигнала, использованного здесь, частоты равны ω_c + ω_s и ω_c − ω_s. Пока несущие частоты соседних радиостанций достаточно разнесены, и боковые полосы не перекрываются между собой, станции не будут влиять друг на друга.