ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ ИЗМЕРЕНИЙ
Случайные погрешности обладают следующими свойствами.
1. При большом числе измерений одинаковые по величине, но противоположные по знаку погрешности встречаются одинаково часто.
2. Большие по величине погрешности встречаются с меньшей вероятностью, чем малые. Из соотношений (1), переписав их в виде
Х = 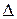 х1+ х1
х1+ х1
Х = 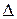 х2 + х2
х2 + х2
……………
Х = 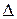 хn + хn
хn + хn
и сложив столбиком, можно определить истинное значение измеряемой величины следующим образом:
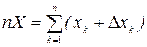 или
или 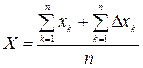 .
.
Если считать, что систематические ошибки устранены, то при бесконечно большом числе измерений вторая сумма в числителе обращается в нуль на основании 1 – го свойства случайных погрешностей. Остается
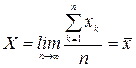 (2)
(2)
т.е. истинное значение измеряемой величины равно среднему арифметическому значению результатов измерений, если их бесконечно много. При ограниченном, а тем более при небольшом числе измерений, с которым мы обычно имеем дело на практике, равенство (2) носит приближенный характер.
Пусть в результате нескольких измерений получены следующие значения измеряемой величины Х: 13,4; 13,2; 13,3; 13,4; 13,3; 13,2; 13,1; 13,3; 13,3; 13,2; 13,3; 13,1. Построим диаграмму распределения этих результатов, откладывая по оси абсцисс показания прибора в порядке их возрастания. Расстояния между соседними точками по оси абсцисс равны удвоенной максимальной ошибке отсчета по прибору. В нашем случае отсчет произведен до 0,1. Этому и равно одно деление шкалы, нанесенной на ось абсцисс. По оси ординат откладываем величины, пропорциональные относительному числу результатов, соответствующих тому или иному показанию прибора. Относительное число, или относительную частоту результатов, равных хк, будем обозначать W(хк). В нашем случае
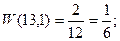
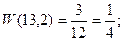

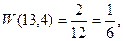
Каждому хк ставим в соответствие
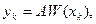 (3)
(3)
где А – коэффициент пропорциональности.
 |
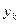
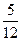
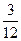
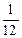
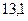
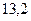
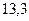
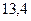
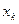
Диаграмма, которую называют гистограммой, отличается от обычного графика тем, что точки не соединены плавной кривой линей, а через них проведены ступеньки. Очевидно, что площадь ступеньки над некоторым значением хк пропорциональна относительной частоте появления этого результата. Выбирая соответствующим образом коэффициент пропорциональности в выражении (3), можно эту площадь сделать равной относительной частоте появления результата хк. Тогда сумма площадей всех ступенек, как сумма относительных частот всех результатов, должна быть равна единице
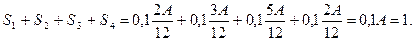 (4)
(4)
Отсюда находим А=10. Условие (4) называется условием нормировки функции (3).
Если производить серии измерений по n измерений в каждой серии, то при небольшом n относительные частоты одного и того же значения хk, найденные из различных серий, могут значительно отличаться друг от друга. По мере увеличения числа измерений в сериях колебания в значениях W(xk) уменьшаются и эти значения приближаются к некоторому постоянному числу, которое называется вероятностью результата хк и обозначается Р(хк).
Допустим, что, производя опыт, мы не отсчитываем результат до целых делений шкалы или их долей, а можем фиксировать ту точку, где остановилась стрелка. Тогда при неограниченно большом числе измерений стрелка побывает в каждой точке шкалы. Распределение результатов измерений приобретает в этом случае непрерывный характер и вместо ступенчатой гистограммы описывается непрерывной кривой y = f(x). На основании свойств случайных погрешностей можно заключить, что кривая должна быть симметрична и, следовательно, максимум ее приходится на среднее арифметическое значение результатов измерений, равное истинному значению измеряемой величины. В случае непрерывного распределения результатов измерений не имеет
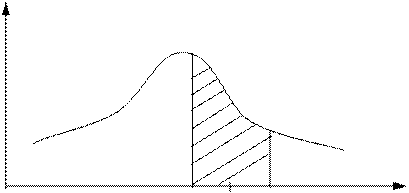 |
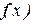
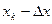
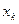
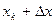
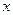
смысла говорить о вероятности какого – либо из их значений, т.к. имеются значения, как угодно близкие к рассматриваемому. Теперь уже следует ставить вопрос о вероятности встретить при измерениях результат в некотором интервале около значения хк, равном 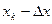 ,
, 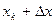 . Подобно тому как на гистограмме относительная частота результата хк равнялось площади ступеньки, построенной над этим результатом, на графике для непрерывного распределения вероятность нахождения результата в интервале (
. Подобно тому как на гистограмме относительная частота результата хк равнялось площади ступеньки, построенной над этим результатом, на графике для непрерывного распределения вероятность нахождения результата в интервале ( 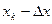 ,
, 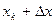 ), равна площади криволинейной трапеции, построенной над этим интервалом и ограниченной кривой f(x). Математическая запись этого результата имеет вид
), равна площади криволинейной трапеции, построенной над этим интервалом и ограниченной кривой f(x). Математическая запись этого результата имеет вид
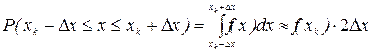 ,
,
если 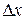 мало, т.е. площадь заштрихованной криволинейной трапеции заменяется приблизительно площадью прямоугольника с тем же основанием и высотой, равной f(хк). Функцию f(х) называют плотностью вероятности распределения результатов измерений. Вероятность найти х на некотором интервале равна плотности вероятности для данного интервала, умноженной на его длину.
мало, т.е. площадь заштрихованной криволинейной трапеции заменяется приблизительно площадью прямоугольника с тем же основанием и высотой, равной f(хк). Функцию f(х) называют плотностью вероятности распределения результатов измерений. Вероятность найти х на некотором интервале равна плотности вероятности для данного интервала, умноженной на его длину.
Кривая распределения результатов измерений, полученная экспериментально для некоторого участка шкалы прибора, если ее продолжить, асимптотически приближая слева и справа к оси абсцисс, аналитически хорошо описывается функцией вида
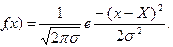 (5)
(5)
Подобно тому как суммарная площадь всех ступенек на гистограмме равнялась единице, вся площадь между кривой f(х) и осью абсцисс, имеющая смысл вероятности встретить при измерениях хоть какое – либо значение х, тоже равна единице. Распределение, описываемое этой функцией, называется нормальным распределением. Основной параметр нормального распределения – дисперсия s2. Приближенное значение дисперсии может быть найдено из результатов измерений по формуле
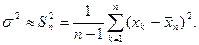 (6)
(6)
Эта формула дает близкое к действительному значение дисперсии только при большом числе измерений. Например, найденное по результатам 100 измерений σ2 может иметь отклонение от действительного значения 15%, найденное по 10 измерениям уже 40%. Дисперсия определяет вид кривой нормального распределения. Когда случайные погрешности малы, дисперсия, как следует из (6), невелика. Кривая f(х) в этом случае уже и острее вблизи истинного значения Х и быстрее стремится к нулю при удалении от него, чем при больших погрешностях. Следующий рисунок покажет, как меняется вид кривой f(х) для нормального распределения в зависимости от σ.
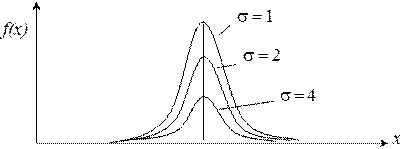 |
х
В теории вероятностей доказывается, что если рассматривать не распределение результатов измерений, а распределение средних арифметических значений, найденных из серии по n измерений в каждой серии, то оно тоже подчиняется нормальному закону, но с дисперсией, в n раз меньшей.
Вероятность нахождения результата измерений в некотором интервале ( 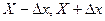 ) около истинного значения измеряемой величины
) около истинного значения измеряемой величины 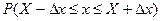 равна площади криволинейной трапеции, построенной над этим интервалом и ограниченной сверху кривой f(x). Величину интервала
равна площади криволинейной трапеции, построенной над этим интервалом и ограниченной сверху кривой f(x). Величину интервала 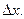 принято измерять в единицах, пропорциональных корню квадратному из дисперсии
принято измерять в единицах, пропорциональных корню квадратному из дисперсии 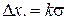 В зависимости от величины k на интервал
В зависимости от величины k на интервал 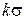 приходится криволинейная трапеция большей или меньшей площади, т.е.
приходится криволинейная трапеция большей или меньшей площади, т.е.
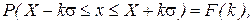 (7)
(7)
где F(k) – некоторая функция от к. Вычисления показывают, что при
k=1, 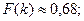
k=2, 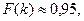
k=3, 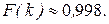
Отсюда видно, что на интервале 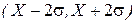 приходится приблизительно 95% площади под кривой f(x). Этот факт находится в полном соответствии со вторым свойством случайных погрешностей, которые утверждает, что большие по величине погрешности маловероятны. Погрешности, превышающие по величине
приходится приблизительно 95% площади под кривой f(x). Этот факт находится в полном соответствии со вторым свойством случайных погрешностей, которые утверждает, что большие по величине погрешности маловероятны. Погрешности, превышающие по величине 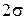 , встречается с вероятностью, меньшей 5%. Переписанное для распределения среднего арифметического значения n измерений выражение (7) принимает вид
, встречается с вероятностью, меньшей 5%. Переписанное для распределения среднего арифметического значения n измерений выражение (7) принимает вид
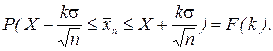 (8)
(8)
Величина 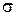 в (7) и (8) может быть определена на основании результатов измерений только приближенно по формуле (6)
в (7) и (8) может быть определена на основании результатов измерений только приближенно по формуле (6)
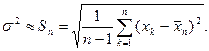
Подставив это значение 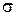 в выражение (8), мы получим справа уже не F(k), а какую – то новую функцию, зависящую не только от величины рассматриваемого интервала значений Х, но и от числа произведенных измерений
в выражение (8), мы получим справа уже не F(k), а какую – то новую функцию, зависящую не только от величины рассматриваемого интервала значений Х, но и от числа произведенных измерений 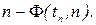 Причем
Причем 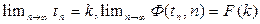
т.к. только при очень большом числе измерений формула (6) становится достаточно точной.
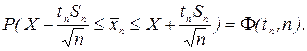
Решив систему двух неравенств, стоящих в скобке в левой части этого выражения относительно истинного значения Х, можем переписать его в виде
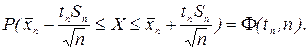 (9)
(9)
Выражение (9) определяет вероятность, с которой истинное значение Х находится в некотором интервале длиной 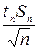 около значения
около значения 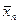 . Эта вероятность в теории ошибок называется надежностью, а соответствующий ей интервал для истинного значения – доверительным интервалом. Функция
. Эта вероятность в теории ошибок называется надежностью, а соответствующий ей интервал для истинного значения – доверительным интервалом. Функция 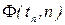 рассчитана в зависимости от tn и n и для нее составлена подробная таблица. Таблица имеет 2 входа: по tn и по n. С ее помощью для данного числа измерений n можно найти, задаваясь определенной величиной надежности Р, значения величины tn, называемой коэффициентом Стьюдента.
рассчитана в зависимости от tn и n и для нее составлена подробная таблица. Таблица имеет 2 входа: по tn и по n. С ее помощью для данного числа измерений n можно найти, задаваясь определенной величиной надежности Р, значения величины tn, называемой коэффициентом Стьюдента.
| tn | tn | tn | tn | tn | |
| n \ P | 0,5 | 0,9 | 0,95 | 0,99 | 0,999 |
| 1,00 | 6,3 | 12,7 | 63,7 | 636,6 | |
| 0,82 | 2,9 | 4,3 | 9,9 | 31,6 | |
| 0,77 | 2,4 | 3,2 | 5,8 | 12,9 | |
| 0,74 | 2,1 | 2,8 | 4,6 | 8,6 | |
| 0,73 | 2,0 | 2,6 | 4,0 | 6,9 | |
| 0,72 | 1,9 | 2,4 | 3,7 | 6,0 | |
| 0,71 | 1,9 | 2,4 | 3,5 | 5,4 | |
| 0,71 | 1,9 | 2,3 | 3,4 | 5,0 | |
| 0,70 | 1,8 | 2,3 | 3,3 | 4,8 |
Анализ таблицы показывает, что для определенного числа измерений с требованием роста надежности получаем растущие значения tn, т.е. увеличение доверительного интервала. Надежности, равной единице, соответствовал бы доверительный интервал, равный бесконечности. Задаваясь определенной надежностью, мы можем сделать доверительный интервал для истинного значения более узким, увеличивая количество измерений, т.к. Sn при этом изменяется незначительно, а 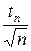 убывает и за счет уменьшения числителя, и за счет увеличения знаменателя. Произведя достаточное количество опытов, можно сделать доверительный интервал любой малой величины. Но при большом n дальнейшее увеличение числа опытов очень медленно уменьшает доверительный интервал, а количество вычислительной работы намного возрастает. Иногда в практической работе удобно пользоваться приближенным правилом: чтобы уменьшить доверительный интервал, найденный по небольшому числу измерений, в несколько раз, нужно увеличить число измерений во столько же раз.
убывает и за счет уменьшения числителя, и за счет увеличения знаменателя. Произведя достаточное количество опытов, можно сделать доверительный интервал любой малой величины. Но при большом n дальнейшее увеличение числа опытов очень медленно уменьшает доверительный интервал, а количество вычислительной работы намного возрастает. Иногда в практической работе удобно пользоваться приближенным правилом: чтобы уменьшить доверительный интервал, найденный по небольшому числу измерений, в несколько раз, нужно увеличить число измерений во столько же раз.
ПРИМЕР ОБРАБОТКИ РЕЗУЛЬТАТОВ ПРЯМЫХ ИЗМЕРЕНИЙ
Возьмем в качестве опытных данных три первых результата из 12, по которым строилась гистограмма Х: 13,4; 13,2; 13,3.
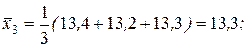
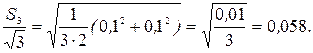
Зададимся надежностью, которая обычно принята в учебной лаборатории, Р = 95%. Из таблицы для Р = 0,95 и n = 3 находим tn = 4,3.
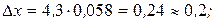
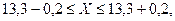 или
или 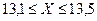
с надежностью 95%. Последний результат принято записывать в виде равенства
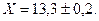
Если доверительный интервал такой величины не устраивает (например в случае, когда приборная погрешность равна 0,1), и мы хотим уменьшить его вдвое, следует увеличить число измерений вдвое.
Если взять, например, последние 6 значений из тех же 12 результатов (для первых шести предлагается проделать расчет самим)
Х: 13,1; 13,3; 13,3; 13,2; 13,3; 13,1,
то 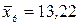
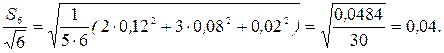
Значение коэффициента tn находим из таблицы для Р = 0,95 и n = 6; tn = 2,6. 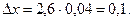
В этом случае 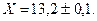 Изобразим на числовой оси доверительный интервал для истинного значения в первом и во втором случаях.
Изобразим на числовой оси доверительный интервал для истинного значения в первом и во втором случаях.
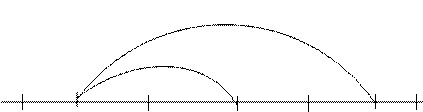
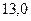
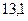
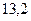
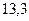
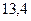
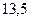
Интервал, рассчитанный по 6 измерениям, находится, как и следовало ожидать, внутри интервала, найденного по трем измерениям.
Приборная погрешность вносит в результаты систематическую ошибку, которая расширяет изображенные на оси доверительные интервалы на 0,1. Поэтому записанные с учетом приборной погрешности результаты имеют вид
1) 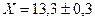 2)
2) 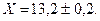
Дата добавления: 2022-02-05; просмотров: 413;











