ИЗМЕРЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН

Лабораторные работы физического практикума посвящены изучению ряда физических явлений. Это изучение состоит в экспериментальном определении некоторых физических величин и проверке соотношений, связывающих их. Измерения физических величин разделяются на прямые и косвенные. К прямым измерениям относятся такие, результаты которых непосредственно считываются со шкалы прибора. Косвенные измерения производятся путем вычислений по формулам, связывающим результаты прямых измерений. При этом мы исходим из того, что существуют точные или “истинные” значения интересующих нас физических величин и пытаемся получить в результате измерений сведения о них. Пусть Х – истинное значение величины, х₁, х₂, …, х_n – результаты n ее измерений. Тогда разности

Х – х₁ = 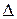х₁,

Х – х₂ = 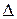х₂, (1)

……………

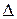Х – х_n = х_n

называются погрешностями или ошибками 1- го, 2- го, …, n- го измерений. Погрешности сопровождают все измерения. Они делятся на систематические, случайные и промахи.

Систематические погрешности – это постоянные по величине и знаку погрешности, которые в каждом последующем измерении либо увеличивают, либо уменьшают результат на одну и ту же величину. Причинами их могут быть ошибки метода измерений, неисправности и неправильная установка приборов, их конструктивные возможности и взаимное влияние, неполный учет влияния всех внешних факторов при выполнении измерений, какое – либо упущение со стороны экспериментатора. Иногда измерения сопровождаются погрешностями, изменяющимися по определенному закону (например, вследствие удлинения отдельных частей прибора в результате их нагревания в процессе работы). Они тоже относятся к систематическим. Систематические погрешности могут быть учтены или исключены, если измерения одних и тех же величин произвести различными методами и приборами с последующим анализом результатов. В учебных лабораториях, как правило, не ставится задача об обнаружении и исключении систематических ошибок.

Случайные погрешности – неопределенные по величине и знаку погрешности, которые нельзя заранее предвидеть и от которых в принципе невозможно избавиться. Они сопровождают любой эксперимент. Причиной их является непостоянство физических условий, в которых производятся измерения, например небольшие колебания температуры воздуха, незначительное сотрясение установки от проезжающих по улицам автомашин, хлопанья дверями в соседних помещениям и т.п., а также ошибки, которые вносят в результаты сам наблюдатель вследствие несовершенства наших органов чувств.

Изучение влияния случайных погрешностей на результаты измерений занимает теория ошибок, которая является разделом теории вероятностей и математической статистики. Приведенные ниже результаты этой теории покажут, как получить при достаточно большом числе измерений значения измеряемых величин, достаточно близкие к истинным значениям.

Промахи – это большие по величине погрешности, сильно искажающих результат. Они являются следствием неправильной записи, неверного отсчета. В теории разработаны приемы, с помощью которых можно подсчитать с определенной вероятностью является ли данный результат промахом или нет. Мы же будем просто отбрасывать сильно отличающие от остальных результаты как не внушающие доверия.

На особом месте стоят погрешности приборов. Это систематические погрешности, т.к. на определенном участке шкалы прибор либо постоянно завышает результат, либо занижает его. Причиной появления их могут быть конструктивные недостатки приборов, неточность в нанесении шкалы, изменения показаний в результате длительной непрерывной работы из – за нагревания прибора и т.п. Знак приборной погрешности обычно неизвестен, а максимальная величина ее задается либо в паспорте к прибору, либо с помощью указания класса точности прибора на его шкале. У электроизмерительных приборов, приборов теплового контроля класс точности прибора равен в процентах отношению максимальной его погрешности к максимальному показанию и обозначается одним из чисел 0,05; 0,1; 0,2; … 4,0. Например, если класс точности вольтметра 0,5 то 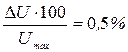т.е.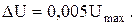

В случае весоизмерительных приборов класс точности обозначается цифрой и последующей за ней буквой. Цифра указывает, в каком разряде после запятой содержится ошибка в относительной погрешности, выраженной в процентах, а буква, - какая цифра стоит в указанном разряде. Буквы а, б, в, г, … соответствуют цифрам 1, 2, 3, 4, … Например, если класс точности весов 2а, значит 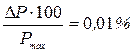для класса 1в - 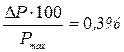. Если погрешность приборов не указана, то в качестве нее берется половина цены наименьшего деления шкалы.

При отсчете по приборам наблюдатель совершает ошибку отсчета. Если он производит отсчет до целых делений, то максимально возможная ошибка отчета равна половине деления, при отсчете до четверти деления – восьмой его части и т.д. Есть ли надобность делить на глаз при отсчете деления прибора на мелкие части? Очевидно нет. Отсчет нужно производить таким образом, чтобы ошибка, допущенная при отсчете, была той же величины или несколько меньше ошибки прибора. Ведь в конечном результате эти ошибки суммируются, и не имеет смысла намного усложнять измерительную работу, отсчитывая малые доли деления, т.к. сумму определит ошибка прибора, которая приблизительно равна половине цены наименьшего деления.

Случайные погрешности проявляют себя в том, что результаты измерений отличаются последними цифрами. Однако при повторных измерениях мы иногда получаем один и тот же результат. Причина этого не в отсутствии случайных погрешностей, а в недостаточной чувствительности прибора. Погрешность прибора в этом случае значительно превышает погрешности случайные. Например, при измерении длины небольшого бруска обычной миллиметровой линейкой заведомо ясно, что каждый раз будет получаться один и тот же результат. При измерении этого же размера микрометром значения последующих измерений возможно будут уже отличаться последними цифрами. Рекомендуется для измерений выбирать такие приборы, которые достаточно чувствительны, и производить возможно большее количество измерений. Используя методы теории ошибок, можем получить с определенной вероятностью тем более близкие к истинному значению результат, чем большее число измерений произведено.