Принимая во внимание (6), уравнение (9) перепишется в виде
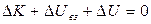 , (10)
, (10)
Поскольку после соударения мы рассматриваем маятник с пулей как недеформируемое целое (т.е. как твердое тело), то для всех 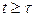
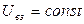 , и поэтому при отклонении маятника на угол
, и поэтому при отклонении маятника на угол 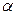
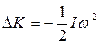 , (11)
, (11)

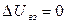 , (12)
, (12)
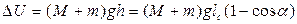 , (13)
, (13)
где 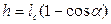 - модуль вертикального перемещения центра инерции маятника с пулей,
- модуль вертикального перемещения центра инерции маятника с пулей, 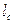 - расстояние от центра инерции маятника с пулей до точки подвеса 0 (см.рис.1.2.1), М – масса маятника без пули.
- расстояние от центра инерции маятника с пулей до точки подвеса 0 (см.рис.1.2.1), М – масса маятника без пули.
Подставляя (11) - (13) в уравнение (10), получаем
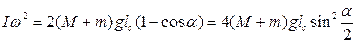 , (14)
, (14)
Согласно определению центра инерции
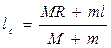 , (15)
, (15)
где R – расстояние от точки 0 до центра инерции маятника без пули. Тогда выражение (14) запишется так:
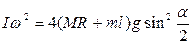 , (16)
, (16)
Выражая далее из (8) 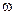 и подставляя его в (16), находим формулу для скорости пули:
и подставляя его в (16), находим формулу для скорости пули:
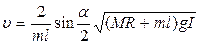 , (17)
, (17)
Момент инерции I находится из формулы для периода колебаний физического маятника: 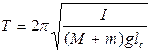 , (см. лаб. работу №1.6),
, (см. лаб. работу №1.6),
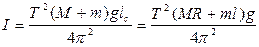 . (18)
. (18)
С учетом выражения (18) формула (17) принимает весьма простой вид:
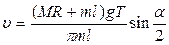 . (19)
. (19)
Если теперь принять во внимание, что 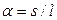 , где s – путь, пройденный свободным концом маятника при его максимальном отклонении от положения равновесия (см.рис.1.2.1.),
, где s – путь, пройденный свободным концом маятника при его максимальном отклонении от положения равновесия (см.рис.1.2.1.), 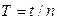 , где t – время n полных колебаний маятника с пулей, а отношение
, где t – время n полных колебаний маятника с пулей, а отношение 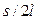 мало, то заменяя
мало, то заменяя 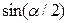 его аргументом, получаем
его аргументом, получаем
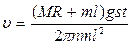 . (20)
. (20)
В выражении (20) все величины, входящие в правую часть, могут быть непосредственно измерены (прямые измерения) и, следовательно, может быть определена скорость пули.
Литература
1. Савельев И.В. Курс общей физики. Т.1.- М.: Наука, 1987, §§ 18 - 24,
27 –29.
2. Савельев И.В. Курс физики. Т.1. – М.: Наука, 1989, §§ 16, 19 – 24,
26, 27.
ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА С ПОМОЩЬЮ ПРИБОРА ОБЕРБЕКА.
Тело, изменением формы которого в процессе движения можно пренебречь, называют абсолютно твердым. В дальнейшим для краткости мы будем называть такое тело просто твердым. Число степеней свободы твердого тела равно шести. Это означает, что требуется шесть независимых величин, однозначно определяющих в каждый момент времени положение тела в пространстве. В качестве таковых можно взять три декартовых координаты центра масс тела и три угла, определяющих его ориентацию в пространстве. В соответствии с этим для описания движения твердого тела в общем случае требуется шесть независимых уравнений движения. Их можно представить в виде двух независимых векторных уравнений:
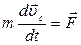 (1)
(1)
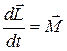 (2)
(2)
где m – масса тела, 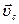 - скорость его центра масс,
- скорость его центра масс, 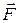 - результирующая внешних сил, действующих на тело,
- результирующая внешних сил, действующих на тело, 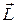 - момент импульса тела относительно некоторой точки,
- момент импульса тела относительно некоторой точки, 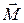 - суммарный момент внешних сил относительно той же точки. Соотношение (1) представляет собой уравнение движения центра масс тела. Соотношение (2) называют уравнением моментов. Оно описывает изменение ориентации тела в пространстве, т.е. его вращение.
- суммарный момент внешних сил относительно той же точки. Соотношение (1) представляет собой уравнение движения центра масс тела. Соотношение (2) называют уравнением моментов. Оно описывает изменение ориентации тела в пространстве, т.е. его вращение.
Зная законы действующих сил и начальные условия, можно с помощью этих уравнений полностью решить задачу о движении тела, т.е. найти как скорость, так и положение каждой точки твердого тела в любой момент времени. Однако решение уравнений (1) и (2) в общем случае представляет собой весьма сложную задачу. При ограничении свободы движения число независимых уравнений, требующихся для описания движения, уменьшается. Одним из частных случаев движения твердого тела является его вращение относительно неподвижной оси. В этом случае изменение положения тела в пространстве описывается только одной величиной – углом поворота тела вокруг этой оси. Для описания такого движения достаточно использовать лишь одно скалярное уравнение - проекцию (2) на ось вращения z:
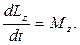 (3)
(3)
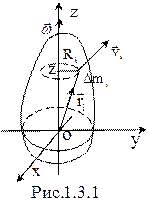 Рассмотрим твердое тело, вращающееся вокруг неподвижной оси Z с угловой скоростью
Рассмотрим твердое тело, вращающееся вокруг неподвижной оси Z с угловой скоростью 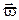 (рис 1.3.1). Найдем проекцию момента импульса тела на ось Z. Разбивая мысленно тело на элементарные массы
(рис 1.3.1). Найдем проекцию момента импульса тела на ось Z. Разбивая мысленно тело на элементарные массы 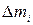 и учитывая, что скорость i-ой элементарной массы при ее вращательном движении
и учитывая, что скорость i-ой элементарной массы при ее вращательном движении
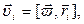
где 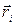 - радиус-вектор i-ой точки тела, для момента импульса тела
- радиус-вектор i-ой точки тела, для момента импульса тела 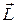 относительно точки О получаем следующее выражение
относительно точки О получаем следующее выражение
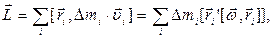 (4)
(4)
где сумма берется по всем элементарным массам тела., перепишем (4) в виде
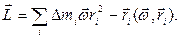 (5)
(5)
Но поскольку 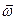 параллелен оси Z, то
параллелен оси Z, то 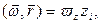 где
где 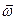 и
и 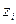 - проекции векторов
- проекции векторов 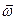 и
и 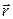 на ось Z соответственно. Проектируя теперь уравнение (5) на ось Z почленно, находим
на ось Z соответственно. Проектируя теперь уравнение (5) на ось Z почленно, находим
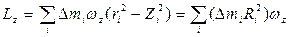 ,
,
где 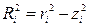 - квадрат расстояния элементарной массы
- квадрат расстояния элементарной массы 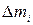 от оси вращения.
от оси вращения.
Величину 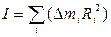 называют моментом инерции тела относительно оси Z (см. лаб. работу №1.5.). Учитывая это, окончательно получим
называют моментом инерции тела относительно оси Z (см. лаб. работу №1.5.). Учитывая это, окончательно получим
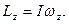 (6)
(6)
С учетом (6) проекция уравнения моментов (3) на ось Z запишется так
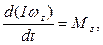
или, поскольку для твердого тела I=const,
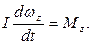 (7)
(7)
Это и есть уравнение вращательного движения твердого тела вокруг неподвижной оси Z. Проекции 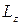 и
и 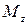 называют соответственно моментами импульса и силы относительно оси Z. Интегрирование уравнений (7) с учетом начальных условий позволяет полностью решить задачу о вращении твердого тела вокруг неподвижной оси – найти зависимость от времени угловой скорости
называют соответственно моментами импульса и силы относительно оси Z. Интегрирование уравнений (7) с учетом начальных условий позволяет полностью решить задачу о вращении твердого тела вокруг неподвижной оси – найти зависимость от времени угловой скорости 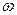 и угла поворота
и угла поворота 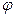 .
.
Уравнение (7) может быть экспериментально проверено на приборе Обербека.
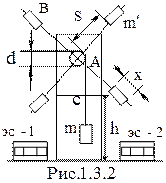 |
Маятник Обербека (рис.1.3.2) состоит из шкива А диаметром d, к которому прикреплены четыре одинаковых стержня В, расположенных под углом 90° друг к другу. На стержнях могут закрепляться одинаковые грузы массой m¢ каждый, которые можно перемещать вдоль стержней, изменяя таким образом момент инерции маятника. На стержни нанесены деления, позволяющие измерять расстояния от грузов m¢ до оси вращения.
Маятник выводится из состояния покоя при помощи груза массой m , подвешенного на нити, намотанной на шкив.
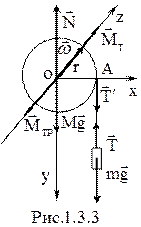 На поступательно движущийся груз действует сила тяжести
На поступательно движущийся груз действует сила тяжести 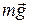 и сила упругости
и сила упругости 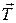 , приложенная со стороны нити (рис. 1.3.3.). На шкив маятника А действует сила тяжести
, приложенная со стороны нити (рис. 1.3.3.). На шкив маятника А действует сила тяжести 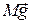 , сила реакции опоры
, сила реакции опоры 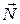 , силы трения в опоре и сила упругости нити
, силы трения в опоре и сила упругости нити 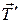 . Моменты сил
. Моменты сил 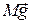 и
и 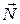 относительно оси Z равны нулю, так обе силы при симметричном расположении грузов m¢ (и без них) на стержнях приложены в точке 0, лежащей на оси. Модули моментов сил трения и упругости (до момента соприкосновения груза со столом) относительно оси Z равны соответственно
относительно оси Z равны нулю, так обе силы при симметричном расположении грузов m¢ (и без них) на стержнях приложены в точке 0, лежащей на оси. Модули моментов сил трения и упругости (до момента соприкосновения груза со столом) относительно оси Z равны соответственно 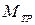 и
и 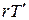 , где r – радиус шкива.
, где r – радиус шкива.
Описание движения системы маятник – нить – груз значительно упростится, если пренебречь массой нити. В этом случае можно считать, что 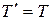 и для описания движения системы достаточно двух уравнений
и для описания движения системы достаточно двух уравнений
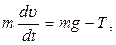 (8)
(8)
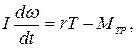 (9)
(9)
где 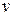 и
и 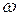 - модули скорости груза и угловой скорости маятника, I- момент инерции маятника относительно оси Z. Здесь учтено также, что
- модули скорости груза и угловой скорости маятника, I- момент инерции маятника относительно оси Z. Здесь учтено также, что 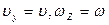 ,
, 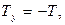
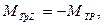
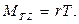
Если теперь предложить, что нить нерастяжима и отсутствует ее проскальзывание при раскручивании шкива, то можно приравнять скорость груза линейной скорости точки шкива в месте касания нити
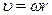 , (10)
, (10)
установив таким образом связь между переменными v и w, входящим в уравнение (8) и (9).
Сначала груз m удерживается на площадке С (рис.1.3.2.), расположенной на высоте h от поверхности стола, причем h можно произвольно изменять. Если площадку убрать, груз m начнет двигаться вниз. Одновременно автоматически включается электросекундомер ЭС-1. В момент касания грузом стола секундомер отключается, зафиксировав время 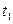 движения груза. Считая движение равноускоренным, находим, используя известный кинематический закон, ускорения груза
движения груза. Считая движение равноускоренным, находим, используя известный кинематический закон, ускорения груза
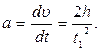 (11)
(11)
Дата добавления: 2022-02-05; просмотров: 402;











