Тригонометрическая форма записи
Геометрический подход к понятию комплексного числа позволяет записывать его в так называемой тригонометрической форме. Для этого вводится понятие модуля и аргумента.
Определение 2.1.Модулем комплексного числа zназывается арифметическое значение корня квадратного из а2 + b2, т. е. | z | = 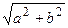 .
.
 Это понятие является обобщением понятия «абсолютная величина действительного числа», так как, если z = a + i · 0, то | z | =
Это понятие является обобщением понятия «абсолютная величина действительного числа», так как, если z = a + i · 0, то | z | = 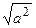 = | а |.
= | а |.
С геометрической точки зрения, модуль комплексного числа – это длина радиус-вектора ОА или расстояние от начала координат до точки с координатами (а, b) (рис. 1).
Определение 2.2.Аргументом комплексного числа z называют угол  между положительным направлением оси
между положительным направлением оси 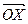 и радиус-вектором
и радиус-вектором 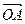 , отсчитываемым против часовой стрелки.
, отсчитываемым против часовой стрелки.
Из этого определения следует, что аргумент комплексного числа определяется неоднозначно, а с точностью до числа, кратного 2 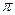 . Поэтому на практике, в качестве аргумента, обычно берут наименьший по абсолютной величине угол, который обозначают
. Поэтому на практике, в качестве аргумента, обычно берут наименьший по абсолютной величине угол, который обозначают  = arg z и находят из соотношений:
= arg z и находят из соотношений:
cos  =
= 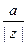 , sin
, sin  =
= 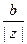 , 0
, 0 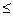

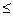 2
2 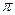
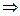 а = | z | · cos
а = | z | · cos  , b = | z | · sin
, b = | z | · sin  ,
,
тогда z = a + i · b = | z | · (cos  + i · sin
+ i · sin  ) и мы получили тригонометрическую форму записи комплексного числа.
) и мы получили тригонометрическую форму записи комплексного числа.
Определение 2.3.Тригонометрической формой записи комплексного числа z называется представление его в виде z = r × (cos  + i × sin
+ i × sin  ), где r = | z | – неотрицательное действительное число,
), где r = | z | – неотрицательное действительное число,  Î[0, 2p).
Î[0, 2p).
Понятие модуля и аргумента комплексного числа z позволяют записать это число в тригонометрической форме.
Пример. Комплексное число z = 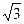 – i записать в тригонометрической форме.
– i записать в тригонометрической форме.
1. Изобразим данное комплексное число на координатной плоскости. Это будет радиус-вектор с концом в точке А ( 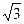 , - 1) (рис. 2)
, - 1) (рис. 2)
 2. Найдем его модуль | z | = |
2. Найдем его модуль | z | = | 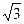 – i | =
– i | = 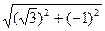 =
= 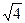 = 2.
= 2.
3. Найдем аргумент из соотношений:
cos  =
= 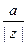 =
= 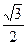 , sin
, sin  =
= 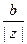 =
= 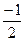
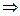
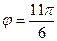 или
или 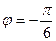
Таким образом, z = 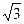 – i = 2 · [cos
– i = 2 · [cos 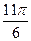 + i · sin
+ i · sin 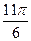 ].
].
Существование двух форм записи одного и того же комплексного числа z = a + i · b = r × (cos  + i × sin
+ i × sin  ) позволяет выполнять алгебраические операции на множестве С в той форме, которая наиболее удобна в каждом конкретном случае.
) позволяет выполнять алгебраические операции на множестве С в той форме, которая наиболее удобна в каждом конкретном случае.
Теорема 2.2.Если z1 = r1 (cos  + i × sin
+ i × sin  ), z2 = r2 (cos
), z2 = r2 (cos 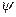 + i × sin
+ i × sin 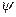 )), то
)), то
1) z1 · z2 = r1 · r2 · [cos 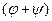 + i × sin
+ i × sin 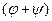 ];
];
2) z1  : z2 =
: z2 = 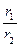 · [cos
· [cos 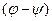 + i × sin
+ i × sin 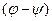 ], где z2
], где z2 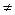 0;
0;
3) если r ¹ 0, то для любого n ÎZ справедлива формула Муавра
zn = rn · [cos( n ·  ) + i × sin (n ·
) + i × sin (n ·  )],
)],
4) 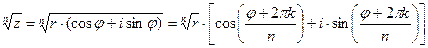 , k = 0, 1, 2, …, (n-1).
, k = 0, 1, 2, …, (n-1).
Операции сложения и вычитания в тригонометрической форме на практике не выполняются.
Пример. Найти (1– i)105.
Имеем 1– i = |1 – i| × (cos  + i × sin
+ i × sin  ), где |1– i| =
), где |1– i| = 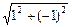 =
= 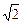 ,
,
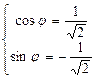 ,
,  =
= 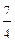 ×p.
×p.
Таким образом, z = 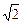 × (cos
× (cos 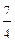 × p + i × sin
× p + i × sin 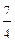 × p)и
× p)и
z105 = ( 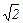 )105× (cos
)105× (cos 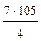 × p + i × sin
× p + i × sin 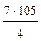 × p) = 250 ×
× p) = 250 × 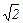 × (cos
× (cos 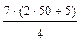 × p + i × ·sin
× p + i × ·sin 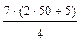 × p) = 250 ×
× p) = 250 × 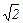 ×(cos
×(cos 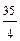 × p + i × sin
× p + i × sin 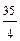 × p) = 250 ×
× p) = 250 × 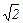 × (cos
× (cos 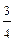 × p + i× sin
× p + i× sin 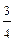 × p ) = 250×
× p ) = 250× 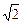 ×(–
×(– 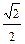 + i ×
+ i × 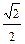 ) = – 250 + i × 250.
) = – 250 + i × 250.
Дата добавления: 2021-12-14; просмотров: 510;











