КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
4.1. Кристаллические и аморфные тела
По своему строению твердые тела делятся на кристаллические и аморфные. Подавляющее большинство твердых тел в природе имеет кристаллическое строение. Так, например, почти все минералы и все металлы в твердом состоянии являются кристаллами. Кристаллические тела отличается повторяемостью в пространстве. Основное отличие кристаллов от жидкостей и газов – анизотропия физических свойств (механических, электрических, оптических и др.). Анизотропиейназывается зависимость свойств от выбранного в материале направления. Причиной анизотропии кристаллов служит упорядоченное расположение частиц (атомов или молекул), из которых они построены. Группа атомов, молекул или ионов образует некоторую элементарную конфигурацию, которая периодически повторяется в трех измерениях без изменения своей ориентации. Таким образом, может быть получен монокристалл макроскопических размеров с правильной внешней огранкой. При этом плоские грани пересекаются под определенными для каждого вида кристалла углами. Говорят, что кристаллы обладают дальним порядком взаимодействия между атомами и молекулами из-за периодичности их структуры.
Однако чаще всего объем кристалла разбит на отдельные разориентированные относительно друг друга области, в пределах которых ориентация элементарной конфигурации сохраняется. Такие тела называются поликристаллическими. У идеальных поликристаллов анизотропия свойств проявляется только в пределах каждого отдельного монокристалла. В целом же идеальный поликристалл не обладает анизотропией вследствие беспорядочной ориентации монокристаллов, из которых он состоит. Однако на практике любая обработка поликристалла (деформация, нагрев, даже процесс роста) приводит к тому, что хаотичность ориентации монокристаллов в поликристаллическом образце нарушается. Возникает так называемая текстура – преимущественная ориентация кристаллов в поликристаллическом образце. При этом природная анизотропия проявляется в той или иной степени.
Кристаллы образуются (растут) из расплавов, паров, растворов исходных веществ, как в природных условиях, так и в лабораторных. В качестве примеров можно привести такие широко известные природные кристаллические материалы, как алмаз (С) и рубин (Al2O3), другие драгоценные камни, кварц (SiO2), каменную соль (NaCl), различные металлы и их соединения. Искусственно можно вырастить монокристаллы даже заданной ориентации. Для этого, например, в расплав каменной соли, цинка и т.д. необходимо поместить небольшой образец кристалла определенной ориентации (затравку) и медленно его из расплава вытягивать. В результате происходит кристаллизация и образуется монокристалл с ориентацией затравки.
Тела, свойства которых одинаковы по всем направлениям, называются изотропными. К ним относятся газы, жидкости и аморфные тела (в переводе с греческого – бесформенные). Аморфные тела представляют собой переохлажденные жидкости с большой вязкостью, что препятствует частицам вещества принятию более упорядоченной формы. Типичные представители данного класса – стекло, различные полимеры, сажа и др. Они отличаются ближним порядком взаимодействия между образующими их частицами.
Интерес ученых к аморфным телам весьма значителен в связи с наличием у них многих полезных свойств. Например, аморфный кремний обладает ценными электронными свойствами.
4.2. Кристаллическая решетка
Выше упоминалось о периодичности строения кристаллических тел. Назовем ту элементарную конфигурацию, которая образована некоторой группой частиц, элементарной кристаллической ячейкой. Тогда при ее многократных параллельных переносах (трансляциях) в трех различных направлениях получится пространственная кристаллическая решетка, т.е. вся решетка состоит из тождественных элементарных ячеек. Такая ячейка представляет собой параллелепипед, построенный на трех наименьших векторах: 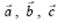 , модули которых равны периодам идентичности (трансляции). А векторы, как известно, можно задать значениями их величин: a, b, c и углами между векторами и осями координат: α, β, γ.
, модули которых равны периодам идентичности (трансляции). А векторы, как известно, можно задать значениями их величин: a, b, c и углами между векторами и осями координат: α, β, γ.
Для описания одной и той же кристаллической структуры элементарную ячейку можно выбрать различными способами. На рис. 4.1 жирными линиями выделены три возможных элементарных ячейки для данной структуры кристалла.
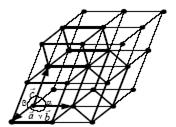
Рис. 4.1.
Кристаллическая решетка обладает трасляционной симметрией, т.е. совпадает сама с собой при перемещениях на величину периодов идентичности. В случае трасляционной симметрии можно задать оператор трансляции
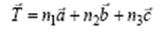 (4.1)
(4.1)
где 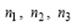 – произвольные целые числа Оператор трансляции
– произвольные целые числа Оператор трансляции 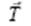 соединяет две точки в кристалле, имеющие одинаковое атомное окружение. Множество операторов трансляции
соединяет две точки в кристалле, имеющие одинаковое атомное окружение. Множество операторов трансляции 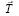 определяет кристаллическую решетку, полученную при параллельном переносе и называемую решеткой Бравэ. Решетка Бравэ является примитивной, если ее ячейки содержат частицы только в вершинах (узлах). Тогда на каждую такую ячейку приходится всего одна частица (одни и те же частицы принадлежат соседним ячейкам одновременно).
определяет кристаллическую решетку, полученную при параллельном переносе и называемую решеткой Бравэ. Решетка Бравэ является примитивной, если ее ячейки содержат частицы только в вершинах (узлах). Тогда на каждую такую ячейку приходится всего одна частица (одни и те же частицы принадлежат соседним ячейкам одновременно).
Но есть вещества, у которых вокруг узла группируется несколько частиц вполне определенным образом. Такие решетки называются решетками с базисом.
При трансляции должна сохраняться периодичность в пространстве как самих узлов, так и окружающего их базиса.
Кристаллические тела обладают не только трасляционной симметрией. Существует симметрия и по отношению к поворотам вокруг некоторых осей (1-го, 2-го, 3-го, 4-го и 6-го порядка). Порядок оси симметрии определяется количеством совпадений решетки с самою собой при повороте на угол 2π.
Существуют и другие виды симметрии, определяемые плоскостью симметрии, винтовой осью n-го порядка и т.д., рассмотрение которых выходит за пределы нашего курса.
Отметим лишь, что в зависимости от формы элементарной ячейки все кристаллы делятся на семь сингоний (кристаллических систем), обладающих определенными классами симметрии. Этим сингониям соответствует 14 возможных пространственных решеток Бравэ.
Далее приведем сингонии кристаллов в порядке возрастания симметрии и соответствующие им параметры и типы решеток Бравэ (рис. 4.2).
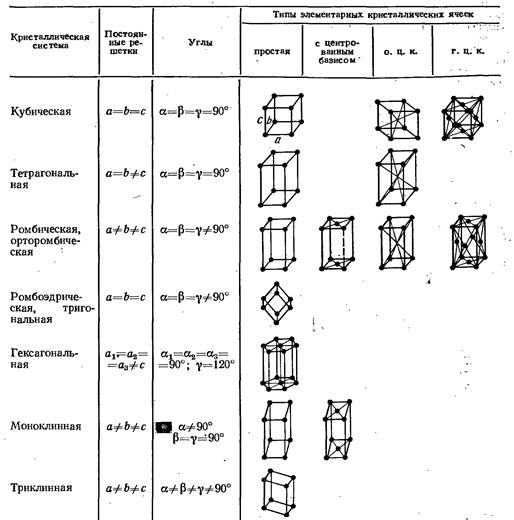
Рис. 4.2. Решетки Бравэ.
Кубическая сингония. 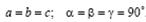 Ячейка примитивная (простая кубическая), объемно-центрированная или гранецентрированная в форме куба.
Ячейка примитивная (простая кубическая), объемно-центрированная или гранецентрированная в форме куба.
Тетрагональная сингония. 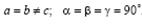 Ячейка примитивная или объемно-центрированная в форме прямой призмы с квадратом в основании.
Ячейка примитивная или объемно-центрированная в форме прямой призмы с квадратом в основании.
Ромбическая сингония. 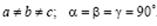 Ячейка примитивная, базоцентрированная, объемно-центрированная или гранецентрированная в форме прямоугольного параллелепипеда.
Ячейка примитивная, базоцентрированная, объемно-центрированная или гранецентрированная в форме прямоугольного параллелепипеда.
Гексагональная сингония. 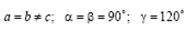 . Примитивная ромбоэдрическая ячейка в форме прямых призм с ромбами в основании. Сложенные вместе три таких ячейки образуют правильную шестигранную призму.
. Примитивная ромбоэдрическая ячейка в форме прямых призм с ромбами в основании. Сложенные вместе три таких ячейки образуют правильную шестигранную призму.
Триклинная сингония. Все параметры разные: 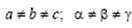 Элементарная ячейка решетки Бравэ примитивная в форме косоугольного параллелепипеда.
Элементарная ячейка решетки Бравэ примитивная в форме косоугольного параллелепипеда.
Моноклинная сингония. 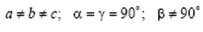 . Ячейка примитивная или базоцентрированная в форме прямой призмы с параллелограммом в основании.
. Ячейка примитивная или базоцентрированная в форме прямой призмы с параллелограммом в основании.
Тригональная (или ромбоэдрическая). 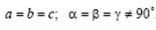 Ячейка ромбоэдрическая примитивная в форме ромбоэдра (куба, деформированного вдоль диагонали) с гранями в виде ромбов.
Ячейка ромбоэдрическая примитивная в форме ромбоэдра (куба, деформированного вдоль диагонали) с гранями в виде ромбов.
4.3. Физические типы кристаллов
Различают четыре типа кристаллов в зависимости от рода частиц в узлах кристаллической решетки.
Ионные кристаллы. В узлах кристаллической решетки расположены ионы противоположного знака. Типичные представители кристаллов данного типа являются каменная соль (NaCl) , MgO и др. В узлах кубической решетки NaCl чередуются положительные ионы натрия (Na+) и отрицательные ионы хлора (Cl−). Между разноименно заряженными ионами существует ионная (гетерополярная) связь, обусловленная их электростатическим взаимодействием. Если в газообразном состоянии NaCl состоит из отдельных молекул, то в кристаллическом весь объем представляет собой как бы одну молекулу (рис. 4.3).
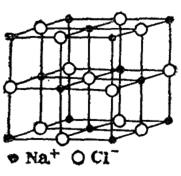
Рис. 4.3.
Атомные кристаллы. В узлах решетки расположены нейтральные атомы, которые связывает между собой гомеополярная (ковалентная) связь квантово-механического происхождения. Эта связь объясняется взаимодействием пар электронов, которые обобществлены парами соседних атомов. Например, C2H4 (рис. 4.4). Типичными представителями данного класса являются алмаз и графит, а также полупроводниковые материалы германий (Ge) и кремний (Si).

Рис. 4.4.
Металлические кристаллы. В узлах решетки – положительные ионы металла, между которыми хаотически движутся свободные электроны, образующие довольно однородное распределение отрицательного заряда в решетке. Между одноименно заряженными ионами существуют силы электростатического отталкивания, которые нейтрализуются зарядами свободных электронов. В результате ионы металла оказываются на расстояниях друг от друга, соответствующих условию равновесия, и кристаллическая решетка становится стабильной (устойчивой) (рис. 4.5).

Рис. 4.5.
Молекулярные кристаллы. В узлах решетки – нейтральные молекулы. Силы связи обусловлены ван-дер-ваальсовским взаимодействием, которое является слабым и имеет место между близко расположенными нейтральными атомами и молекулами, проявляется при отсутствии других, более сильных, видов взаимодействия. К молекулярным кристаллам относятся много веществ, например, кристаллы инертных газов (Ne, Ar, Kr, Xe), Н2, N2, O2, F2, CO2, H2O в твердом состоянии (рис.4.6).
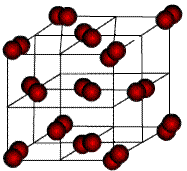
Рис. 4.6. Молекулярный кристалл аргона.
4.3. Дефекты кристаллического строения
При росте кристаллов, как в природных, так и в искусственно созданных условиях никогда не образуется идеальная кристаллическая решетка в силу влияния реальных внешних условий и различных внутренних факторов. Нарушается периодичность расположения ее элементов. В исходном материале могут оказаться примеси, которые внесут свои искажения и т.д. Решетка уже выращенного кристалла страдает в результате приложения внешних механических нагрузок и других воздействий.
Все дефекты в зависимости от их геометрии можно разделить на три группы: точечные, линейные, поверхностные и объемные.
Точечные дефекты – это локальные нарушения решетки в изолированных друг от друга точках пространства. К ним относятся вакансии (рис. 4.7, а), междоузельные атомы (рис. 4.7, б), примеси атомов внедрения и замещения (рис. 4.7, в). Сюда же можно отнести и комплексы примесных атомов различных сортов, лишь бы не нарушалось общепринятое требование к размерам точечного дефекта – не более нескольких межатомных расстояний в любом направлении (рис. 4.7).
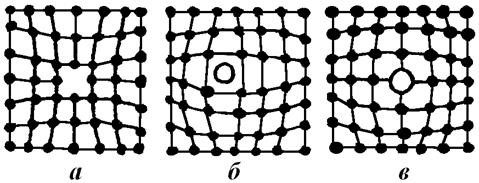
Рис. 4.7. Точечные дефекты кристаллов: вакансия (а); межузельный атом (б); атом замещения (в).
Линейные дефекты:
Основными линейными дефектами являются дислокации. Дислокации – это дефекты кристаллического строения, которые являются линиями, вдоль и вблизи которых нарушенное характерное для кристалла правильное расположение атомных плоскостей.
Простые виды дислокаций – краевые и винтовые.
Краевая дислокация является линией, вдоль которой обрывается внутри кристалла край “лишней“ полуплоскости (рис. 4.8)
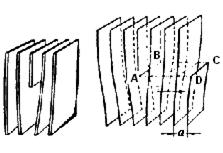
а) б)
Рис. 4.8. Краевая дислокация (а) и механизм ее образования (б)
Неполная плоскость называется экстраплоскостью.
Большинство дислокаций образуются путем механизма сдвига. Ее создание можно описать посредством следующей операции. Надрезать кристалл по плоскости АВСD, сдвинуть нижнюю часть относительно верхних на один период в направлении, перпендикулярном АВ, а затем снова сблизить атомы на краях разреза внизу.
Наибольшие искажения в расположении атомов в кристалле имеют место вблизи нижнего края екстраплоскости. Вправо и влево от края экстраплоскости эти искажения малы (несколько периодов решетки), а вдоль края экстраплоскости искажения тянутся через весь кристалл и могут быть очень большие (тысячи периодов решетки) (рис. 4.8).
Другой тип дислокаций был описан Бюргерсом, и получил название винтовая дислокация.
Винтовая дислокация получена посредством частичного сдвига по плоскости Q вокруг линии EF (рис. 4.9).

Рис. 4.9. Механизм образования винтовой дислокации
На поверхности кристалла образуется ступенька, которая проходит от точки Е к краю кристалла. Такой частичный сдвиг нарушает параллельность атомных слоев, кристалл превращается в одну атомную плоскость, закрученную по винту в виде полого геликоида вокруг линии EF, которая представляет границу, что отделяет часть плоскости скольжения, где сдвиг уже произошел, от части, где сдвиг не начинался. Вдоль линии EF наблюдается макроскопический характер области несовершенства, в других направлениях ее размеры составляют несколько периодов.
Если переход от верхних горизонтов к нижним осуществляется поворотом по часовой стрелке, то дислокация правая, а если поворотом против часовой стрелки – левая.
Если в кристалле дислокации отсутствуют или их количество мало, то пластическая деформация затруднена, и прочность кристаллов велика. Наличие дислокаций в кристалле облегчает пластическую деформацию, которая осуществляется путем скольжения дислокаций. Однако, если дислокаций очень много, то при скольжении они мешают друг другу, и пластическая деформация затрудняется. Поэтому существует два способа упрочнения кристаллов:
1) получение бездефектных кристаллов. В настоящее время созданы кристаллы без дефектов – нитевидные кристаллы длиной до 2 мм, толщиной 0,5…20 мкм – “усы“ с прочностью, близкой к теоретической: для железа 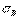 = 13000 МПа, для меди
= 13000 МПа, для меди 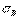 =30000 МПа.
=30000 МПа.
2) увеличение количества дислокаций путем внешней обработки (прокатка, закалка и т. п).
Дислокации влияют не только на прочность и пластичность, но и на другие свойства кристаллов. С увеличением плотности дислокаций растет внутреннее трение, изменяются оптические свойства, повышается электросопротивление металла. Дислокации увеличивают среднюю скорость диффузии в кристалле, убыстряют старение и другие процессы. Дислокации уменьшают химическую стойкость, поэтому в результате обработки поверхности кристалла специальными веществами в местах выхода дислокаций образуются ямки.
Образуются дислокации при пластической деформации, в процессе кристаллизации, при термической обработке.
Поверхностные, или двумерные, дефектыотносятся уже к разряду макроскопических - это границы раздела и дефекты упаковки. Границы раздела являются переходной областью шириной до нескольких десятков межатомных расстояний. В этой области решетка одного зерна, которое имеет определенную ориентацию кристаллографии, переходит в решетку другого зерна, которое имеет другую ориентацию кристаллографии (рис. 4.10). Поэтому на грани зерна наблюдается искаженное кристаллическое строение. Кроме того, по границам зерен в технических металлах скапливаются примеси, что еще больше нарушает правильный порядок расположения атомов.
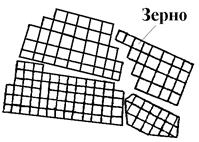
Рис. 4.10. Схема строения поликристалла.
Трехмерные или объемные дефекты– это трещины, дендриты, включения других кристаллов, газов, жидкостей и т.д., а также пустоты. Объемные дефекты – это макродефекты, которые являются изолированными в кристалле участками объема, которые существенно превышают объем элементарной ячейки кристалла.
Дендриты - это древовидные кристаллические образования, которые оказываются в монокристаллах и слитках металлов, полуметаллов, полупроводников и их сплавов (рис 4.11). Максимальная скорость роста кристаллов наблюдается по таким плоскостям и направлениям, которые имеют наибольшую плотность упаковки атомов. В результате растут длинные ветви, которые называют осями первого порядка. На осях первого порядка появляются и начинают расти ветви второго порядка, от которых ответвляются оси третьего порядка. В последнюю очередь идет кристаллизация в участках между осями дендрита.
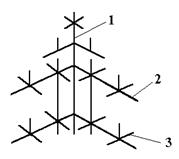
Рис. 4.11. Схема строения дендрита: 1, 2, 3 - оси первого, второго и третьего порядка.
4.4. Тепловое движение в кристаллах.
Узлы кристаллической решетки определяют средние положения частиц. Сами же частицы (ионы, атомы или молекулы) непрерывно колеблются около этих средних положений, причем интенсивность колебаний растет с температурой. Взаимодействие между частицами любого вида может быть представлено потенциальной кривой, изображенной на рис. 4.12.
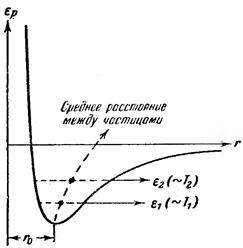
Рис. 4.12. Энергия взаимодействия атомов в кристалле.
Кривая несимметрична относительно минимума. По этой причине только очень малые колебания частиц около положения равновесия будут иметь гармонический характер. С ростом амплитуды колебаний (что происходит при повышении температуры) все сильнее будет проявляться ангармоничность (то есть отклонение колебаний от гармонических). Это приведет, как видно на рис. 4.12, к возрастанию средних расстояний между частицами и, следовательно, к увеличению объема кристалла. Так объясняется тепловое расширение кристаллов.
4.6. Теплоемкость кристаллов.
Расположение частиц в узлах кристаллической решетки отвечает минимуму их взаимной потенциальной энергии. При смещении частиц из положения равновесия в любом направлении появляется сила, стремящаяся вернуть частицу в исходное положение, вследствие чего возникают колебания частицы. Колебание вдоль произвольного направления можно представить как наложение колебаний вдоль трех взаимно перпендикулярных направлений. Поэтому каждой частице в кристалле следует приписать три колебательные степени свободы.
Как следует из закона о равномерном распределении энергии по степеням свободы, на каждую степень свободы частицы приходится в среднем 1/2 кТ. При этом следует учесть, что колебательная степень свободы должна обладать вдвое большей энергетической емкостью по сравнению с поступательной и вращательной. Это объясняется тем, что поступательное и вращательное движение связано с наличием только кинетической энергии, в то время как колебательное движение связано с наличием и кинетической. И поступательной энергией, причем для гармонического колебания среднее значение кинетической и потенциальной энергии оказывается одинаковым. Поэтому на каждую колебательную степень свободы приходится в среднем две половинки кТ – одна в виде кинетической энергии и одна в виде потенциальной. Следовательно, на каждую частицу – атом в атомной решетке, ион в ионной или металлической решетке – приходится в среднем энергия, равная 3кТ. Энергию моля вещества в кристаллическом состоянии можно найти, умножив среднюю энергию одной частицы на число частиц, помещающихся в узлах кристаллической решетки. Последнее число совпадает с числом Авогадро NA только в случае химически простых веществ. В случае такого, например, вещества, как NaCl, число частиц будет равно 2NA, так как в моле NaCl содержится NA атомов Na и NA атомов Cl.
Ограничившись рассмотрением химически простых веществ, образующих атомные и металлические кристаллы, для внутренней энергии моля вещества в кристаллическом состоянии можно написать выражение:
Uμ = NA3kT = 3RT. (4.2)
Приращение внутренней энергии, соответствующее повышению температуры на один кельвин, равно по определению теплоемкости при постоянном объеме. Следовательно,
СV = 3R. (4.3)
Поскольку объем твердых тел при нагревании меняется мало, то их теплоемкость при постоянном давлении незначительно отличается от теплоемкости при постоянном объеме, так что можно считать, что
Сp ≈ СV.
Таким образом, теплоемкость моля химически простых кристаллических веществ одинакова и равна 3R. Это утверждение составляет содержание закона Дюлонга и Пти,установленного опытным путем. Закон выполняется с довольно хорошим приближением при комнатной температуре для многих веществ. Однако, например, алмаз имеет при комнатной температуре теплоемкость, равную всего примерно 0,7R.
Более того, вопреки соотношению (4.3) теплоемкость кристаллов зависит от температуры, причем имеет характер, показанный на рис. 4.13.
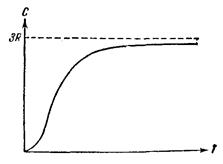
Рис. 4.13.
Вблизи абсолютного нуля теплоемкость всех тел пропорциональна Т3, и только при достаточно высокой, характерной для каждого вещества температуре начинает выполняться равенство (4.3). У большинства веществ это достигается уже при комнатной температуре, у алмаза же теплоемкость достигает значения 3R лишь при температуре порядка 10000С.
Строгая теория теплоемкости твердых тел, созданная Эйнштейном и Дебаем, учитывает, во-первых, квантование энергии колебательного движения. Во-вторых, теория учитывает, что колебания частиц в кристаллической решетке не являются независимыми. Эта теория находится в хорошем согласии с опытными данными. В частности, для высоких температур она приводит к выражению (4.3).
Дата добавления: 2021-12-14; просмотров: 435;











