Третий закон термодинамики (тепловой закон Нернста)

Как уже указывалось, первый и второй законы термодинамики были сформулированы как принципы невозможности двигателей первого и второго рода. Третий закон термодинамики сформулирован как принцип невозможности достижения абсолютного нуля температур.

Рассматривая максимально возможные теплоту и работу химических реакций вблизи абсолютного нуля температуры, немецкий физик и физико-химик В. Нернст (1864–1941) заметил, что для конденсированных систем при T → 0 производные теплоты и работы по температуре становятся равными друг другу и также стремятся к нулю. Базируясь на этом, он своей теоремой (теорема Нернста) установил, что вблизи абсолютного нуля температуры значение всех теплоемкостей становится равным нулю и энтропии S всех веществ, находящихся в равновесном состоянии, становятся неизменными и равными между собой. Этот вывод, называемый тепловым законом Нернста, в дальнейшем подтвержден практикой расчетов и экспериментальными данными определения теплоемкостей. В дальнейшем М. Планк показал, что абсолютные значения энтропии при T → 0 для различных веществ не только равны друг другу, но и могут быть приняты равными нулю, т. е. для всех веществ при T → 0 имеем S₀= 0.

Из вышеуказанного рассуждения следует, что ни путем отвода тепла (т. е. охлаждением тела), ни путем совершения какой-либо работы вблизи абсолютного нуля понизить температуру тела невозможно. Этот вывод формулируется как весьма важный закон: абсолютный нуль температуры недостижим. Опыт показывает, что, говоря словами самого Нернста, «в соответствии с результатами квантовой теории для каждого твердого тела существует в окрестности абсолютного нуля некий температурный интервал, в котором само понятие температуры практически теряет смысл». Или, проще говоря, в этом температурном интервале свойства тела (объём, тепловое расширение, сжимаемость и т.д.) не зависят от температуры. Это поле термической нечувствительности различно у разных тел; у алмаза, согласно Нернсту, оно простирается не менее чем на 40 градусов от абсолютного нуля.

ЖИДКОЕ СОСТОЯНИЕ

3.1. Строение жидкостей

Твердое, жидкое и газообразное состояния веществ различаются, прежде всего, подвижностью атомов и молекул, из которых состоят эти вещества. В газах и жидкостях частицы совершают хаотическое поступательное движение, а в твердых веществах - колебательное движение вокруг положения равновесия. Различие между газами и жидкостями заключается в том, что в жидкостях расстояние между молекулами сравнимо с их размерами, и поэтому потенциальная энергия взаимодействия молекул сравнима по величине с энергией их теплового движения. Это приводит к тому, что тепловое движение молекул жидкости затруднено по сравнению с молекулами газа. Потенциальная энергия взаимодействия молекул жидкости недостаточна, чтобы сохранить устойчивую межмолекулярную структуру, как это наблюдается для твердых тел. Поэтому в жидкостях, в отличие от твердых кристаллических тел, в которых существует дальний порядок, наблюдается только некоторое упорядочение положения близлежащих частиц, то есть ближний порядок. По этой причине жидкость легко принимает форму сосуда, предоставленного ей. Это отличает её от твердых кристаллических тел, в которых существует упорядоченная межатомная структура - кристаллическая решетка.

3.2. Явления на границе раздела газа, жидкости и твердого тела

Опыт показывает, что поверхность жидкости стремится принять такую форму, чтобы иметь минимальную площадь. Это явление связано с воздействием на поверхность жидкости механических сил, стремящихся уменьшить площадь этой поверхности. Указанные силы называются силами поверхностного натяжения.

Рассмотрим явления, возникающие на границе раздела жидкости и газа. Пусть имеется пленка жидкости (например, мыльная пленка), натянутая на рамку с одной подвижной перемычкой (см. рис. 3.1).

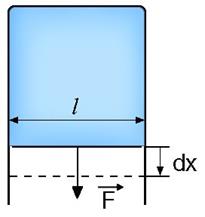
Рис. 3.1. Рамка с жидкой пленкой.

За счет сил поверхностного натяжения пленка будет стремиться уменьшить свою площадь. Для того, чтобы воспрепятствовать этому, к перемычке необходимо приложить силу 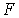, величина которой, как показывает опыт, не зависит от площади пленки, а пропорциональна длине перемычки :

.

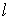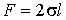(3.1)

Коэффициент пропорциональности 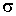называется поверхностным натяжением (коэффициентом поверхностного натяжения). Двойка в формуле (3.1) означает, что пленка жидкости имеет две поверхности и если её толщина много больше межмолекулярного расстояния, то происходит независимое воздействие двух поверхностей пленки на перемычку. Очевидно, что сила 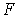равна силе поверхностного натяжения и поэтому из формулы (7.8) следует, что величина силы поверхностного натяжения численно равна произведению поверхностного натяжения 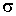на длину линии контакта пленки и перемычки 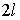. Эта сила направлена по касательной к поверхности пленки.

При медленном перемещении перемычки на величину 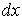, площадь поверхности пленки увеличивается на величину

.

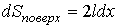(3.2)

Требование медленности перемещения перемычки позволяет считать рассматриваемый процесс изотермическим и квазистатическим (обратимым).

С учетом выражения (3.2) элементарная работа 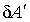, которую необходимо совершить против сил поверхностного натяжения, определяется по формуле

.

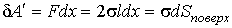(3.3)

Соответственно работа 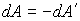, совершаемая силами поверхностного натяжения примет вид

.

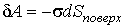(3.4)

Из формулы (3.3) следует, что поверхностное натяжение численно равно работе, которую необходимо затратить при обратимом изотермическом процессе для увеличения площади поверхности жидкости на единицу. Указанная работа затрачивается на приращение энергии поверхности жидкости – свободной поверхностной энергии. Следовательно, поверхностное натяжение численно равно удельной (на единицу площади) свободной поверхностной энергии.

Выясним, чем обусловлено свойство сокращения поверхности жидкости. На рис. 3.2 изображены три молекулы и сферы их действия. Молекулярные силы, действующие на молекулу 1 со стороны молекул, находящихся в сфере молекулярного действия, взаимно уравновешиваются. В иных условиях оказывается молекула 2 на поверхности жидкости. Над ней имеется пар жидкости, действием молекул которого можно пренебречь. При таком условии молекулярные силы, действующие на молекулу 2, оказываются неуравновешенными, их равнодействующая R направлена в глубь жидкости перпендикулярно к её поверхности. В таком состоянии находятся все молекулы поверхностного слоя толщиной в радиус сферы молекулярного действия (приблизительно слой в 1-2 молекулы).

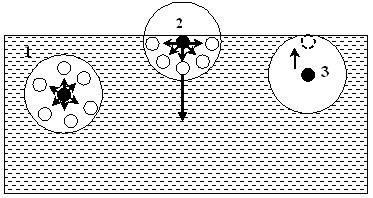
Рис. 3.2. Действие молекулярных сил.

Чтобы молекула 3 оказалась в поверхностном слое жидкости, над ней надо совершить работу против сил, втягивающих её в глубь жидкости. Эта работа совершается за счёт кинетической энергии окружающих её молекул; в результате работы увеличивается потенциальная энергия поверхностного слоя жидкости.

Оказавшись в поверхностном слое, молекула станет обладать большей потенциальной энергией, чем молекулы, расположенные в глубине жидкости. Таким избыточным запасом потенциальной энергии обладают все молекулы поверхностного слоя жидкости. Эта энергия прямо пропорциональна величине поверхности жидкости.

Состояние равновесия жидкости, в отсутствие сил гравитационного притяжения и других внешних сил, имеет место при минимальной площади поверхности, соответствующей заданному объему жидкости. Этим объясняется то, что в невесомости капля жидкости принимает шарообразную форму. Мыльный пузырь имеет почти сферическую форму вследствие малости своего веса.

3.3. Явление смачивания и несмачивания

Рассмотрим теперь явления, происходящие с каплей жидкости, помещенной на поверхность твердого тела. В этом случае имеются три границы раздела между фазами: газ-жидкость, жидкость – твердое тело и газ – твердое тело. Поведение капли жидкости будет определяться значениями поверхностного натяжения (удельными величинами свободной поверхностной энергии) на указанных границах раздела. Сила поверхностного натяжения на границе раздела жидкости и газа будет стремиться придать капле сферическую форму. Это произойдет в том случае, если поверхностное натяжение на границе раздела жидкости и твердого тела будет больше поверхностного натяжения на границе раздела газа и твердого тела (см. рис. 3.3 (а)).

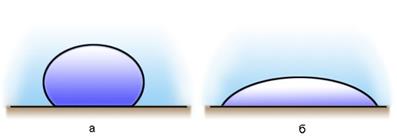
Рис. 3.3. Различные формы капли на поверхности твердого тела для случаев несмачивающей (а) и смачивающей (б) жидкостей

В этом случае процесс стягивания жидкой капли в сферу приводит к уменьшению площади поверхности границы жидкость – твердое тело при одновременном увеличении площади поверхности границы газ-жидкость. Тогда наблюдается несмачивание поверхности твердого тела жидкостью. Форма капли будет определяться равнодействующей сил поверхностного натяжения и силы тяжести. Если капля большая, то она будет растекаться по поверхности, а если маленькая - стремиться к шарообразной форме.

Если поверхностное натяжение на границе раздела жидкости и твердого тела меньше поверхностного натяжения на границе раздела газа и твердого тела, то капля приобретет такую форму, чтобы уменьшить площадь поверхности границы раздела газ-твердое тело, то есть будет растекаться по поверхности тела (см. рис. 3.3 (б)). В этом случае наблюдается смачивание жидкостью твердого тела.

Для количественного описания смачивания жидкостью твердого тела рассмотрим равновесие сил, действующих на элемент 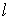контура, образованного пересечением трех границ раздела фаз: газа 1, жидкости 2 и твердого тела 3 (см. рис. 3.4).

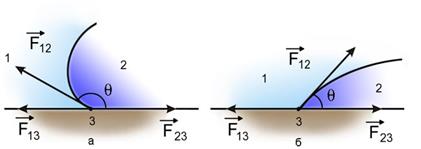
Рис. 3.4. Схемы к расчету равновесия капли на поверхности твердого тела для случаев несмачивающей (а) и смачивающей (б) жидкостей 1 - газ, 2 - жидкость, 3 - твердое тело

Для случая механического равновесия имеем

,

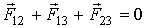(3.5)

где:

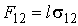,	(3.6)
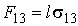,	(3.7)
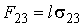,	(3.8)

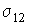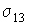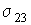а величины , и - равны поверхностному натяжению на границах раздела газ-жидкость, газ-твердое тело и жидкость-твердое тело.

В проекции на горизонтальную ось формулы (3.6) - (3.8) позволяют записать условие равновесия (см. рис 3.4)

,

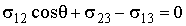(3.9)

где проведено сокращение на величину длины элемента контура .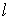

Из формулы (3.9) имеем

.

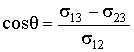(3.10)

Как следует из этой формулы, равновесию жидкости на поверхности твердого тела соответствует вполне определенный угол 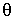, который называется краевым углом. Этот угол может принимать значения от 0 до .

Так как 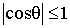, то из формулы (3.10) следует условие существования устойчивого равновесия жидкости на поверхности твердого тела:

.

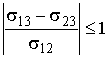(3.11)

Если это условие не выполняется, то капля либо начинает неограниченно (до толщины нескольких мономолекулярных слоев) растекаться по поверхности при

,

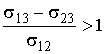(3.12)

, либо стягиваться до тех пор, пока её общая граница с поверхностью не превратится в точку, при

,

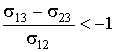(3.13)

В первом случае наблюдается явление полного смачивания твердого тела жидкостью (например, капля керосина на поверхности стекла), а во втором - полное несмачиваение (например, капля воды на поверхности парафина). Если краевой угол 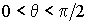, то имеет место частичное смачивание, а при 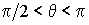- частичное несмачивание.

3.4. Давление под изогнутой поверхностью жидкости

Рассмотрим поверхность жидкости, опирающуюся на некоторый плоский контур (рис. 3.5,а).

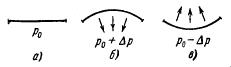
Рис. 3.5.

Если поверхность жидкости не плоская, то стремление ее к сокращению приведет к возникновению давления, дополнительного к тому, которое испытывает жидкость с плоской поверхностью. В случае выпуклой поверхно­сти это дополнительное давление положительно (рис. 3.5, 6), в случае вогнутой поверхности — отрицательно (рис. 3.5, в). В последнем случае поверхностный слой, стремясь сократиться, растягивает жидкость.

Величина добавочного давления, очевидно, должна возрастать с увеличением коэффициента поверхностного натяжения а и кривизны поверхности. Вычислим доба­вочное давление для сферической поверхности жидко­сти. Для этого рассечем мысленно сферическую каплю жидкости диаметральной плоскостью на два полушария (рис. 3.6).

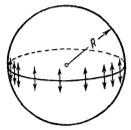
Рис. 3.6. К расчету давления Лапласа.

Из-за поверхностного натяжения оба полушария притягиваются друг к другу с силой, равной

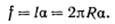(3.14)

Эта сила прижимает друг к другу оба полушария по поверхности S = πR² и, следовательно, обусловливает дополнительное давление

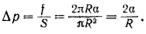(3.15)

Кривизна сферической поверхности всюду одинакова и определяется радиусом сферы R. Очевидно, что чем меньше R, тем больше кривизна сферической поверхности. Кривизну произвольной поверхности принято характеризовать так называемой средней кривизной, которая может оказаться различной для разных точек поверхности.

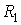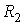В случае, если поверхность имеет произвольную форму и характеризуется двумя главными радиусами и , то:

.

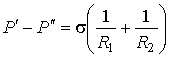(3.16)

Выражение (3.16) является обобщением формулы Лапласа (3.15) на случай произвольной формы поверхности жидкости.

Если поверхность жидкости имеет цилиндрическую форму, то один из радиусов в формуле (3.16) становится бесконечным, и для этого случая формула (3.16) приобретает вид

,

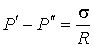(3.17)

где: 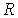- радиус цилиндрической поверхности жидкости.

3.4. Капиллярные явления.

Явление смачивания (или несмачивания) твердого тела жидкостью приводит к появлению капиллярного эффекта. Капилляром называется тонкая трубка, вставленная в сосуд с жидкостью. Капиллярный эффект связан с тем, что в зависимости от того, смачивает жидкость стенки капилляра или нет, внутри капилляра поверхность жидкости приобретает соответственно вогнутую или выпуклую форму(рис. 3.7).

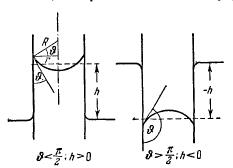
Рис. 3.7. .Капилляр в смачивающей (а) и не смачивающей (б) жидкостях

В первом случае давление внутри жидкости уменьшается по сравнению с внешним давлением, и она поднимается внутри капилляра (см. рис. 3.7 (а)). А во втором - это давление возрастает, что приводит к опусканию уровня жидкости в капилляре по отношению к её уровню в сосуде (см. рис. 3.7 (б)).

Между жидкостью в капилляре и широком сосуде устанавливается такая разность уровней h, чтобы гидро­статическое давление pgh уравновешивало капиллярное давление Δр:

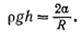(3.18)

В этой формуле а — поверхностное натяжение на границе жидкость —газ, R — радиус кривизны мениска,

Радиус кривизны мениска R можно выразить через краевой угол и радиус капилляра г. В самом деле, из рис. 3.7 видно, что R = г/cos θ. Подставив это значение в (3.18) и разрешив получившееся уравнение относительно h, приходим к формуле

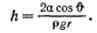(3.19)

В соответствии с тем, что смачивающая жидкость поднимается по капилляру, а несмачивающая — опускается, формула (3.19) дает в случае θ < π/2 (cosθ >0) положительные h и в случае θ >π/2 (cosθ < 0) отрицательные h.

Задача 7.1. Найти силу притяжения двух квадратных пластинок, между которыми находится слой жидкости, толщиной 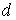. Размер пластинок 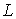много больше толщины слоя жидкости. Коэффициент поверхностного натяжения жидкости равен σ. Считать, что жидкость полностью смачивает пластинки.

Решение: В соответствии с формулой Лапласа (3.15) для случая цилиндрической формы поверхности жидкости имеем выражение для разности атмосферного давления и давления внутри жидкости:

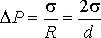
Отсюда

.

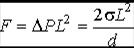По мере уменьшения толщины слоя жидкости, величины и растут, и это приводит к тому, что капля жидкости стремится максимально растечься между пластинами. Минимальная толщина слоя жидкости будет определяться степенью параллельности поверхностей пластинок и качеством их обработки. Чем лучше отшлифованы пластинки, тем сильнее они притягиваются. Для случая воды, находящейся между стеклянными пластинками, разность давлений может достигать величины атмосферного давления.

Отметим, что, несмотря на достаточно большую силу притяжения пластинок, их можно легко рассоединить, сдвигая друг относительно друга вдоль плоскости поверхности.

Задача 7.2.Найти радиус R пузырька газа, находящегося в воде при температуре T с поверхностным натяжением σ, если величина гидростатического давления воды P₀, а концентрация молекул газа равна n. Пузырек считать сферическим, а газ - идеальным.

Решение: Согласно формуле Лапласа (3.15), давление газа в сферическом пузырьке равно

.

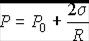В соответствии с основным уравнением молекулярно-кинетической теории

.

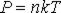Поэтому имеем

.

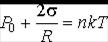Следовательно

.

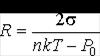Очевидно, что давление газа в пузырьке больше гидростатического давления воды на величину давления, создаваемого поверхностным натяжением.