Применение первого закона термодинамики к изопроцессам.

Для изотермического процесса ΔТ = 0. Следовательно, и ΔU = 0, согласно (2.2). В таком случае (2.10) преобразуется к виду

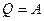. (2.12)

Количество теплоты Q, полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам.

Для изобарного процесса p = const, A = p∙ΔV. Соотношение (2.10) имеет вид

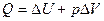. (2.13)

При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T₂ < T₁; внутренняя энергия убывает, ΔU < 0.

Для изохорного процесса ΔV = 0. А = 0. Соотношение (2.10) имеет вид

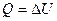. (2.14)

Это означает, что все количество теплоты, переданное системе, идет на измерение ее внутренней энергии. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (Q < 0).

2.5. Теплоемкость идеального газа

Теплоемкость тела - это отношение тепла, сообщенного телу, к изменению температуры δТ, которое при этом произошло:

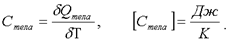(2.15)

Удельная теплоемкость - это отношение теплоемкости тела к его массе, т.е.:

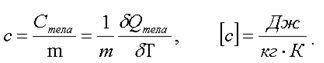(2.16)

Молярная теплоемкость - это теплоемкость одного моля вещества, т.е.:

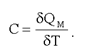(2.17)

Здесь δQ_М – количество тепла, подведенное к одному молю вещества для нагревания его на δТ. Так как масса одного моля равна μ, из (2.29) можно получить связь между С и с:

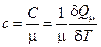; С = с∙μ; С_тела = c (m/μ) (2.18)

Молярная теплоемкость идеального газа при постоянном объеме. Согласно первому началу термодинамики:

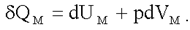(2.19)

При постоянном объеме dVμ = 0 и δQ_М = dU_М.

Отсюда:

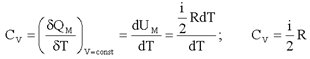(2.20)

Здесь использовано то, что, согласно (2.1),

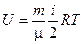и ,

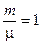если речь идет об одном моле вещества.

Из (2.20) и (2.2) следует:

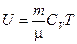(2.21)

Молярная теплоемкость идеального газа при постоянном давлении:

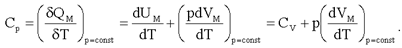(2.22)

Для одного моля уравнение Клапейрона-Менделеева принимает вид:

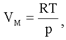
отсюда и из (2.22):

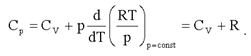
Таким образом:

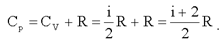(2.23)

Отношение теплоемкостей 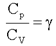называют коэффициентом Пуассона.

Из (2.20) и (2.23) следует, что:

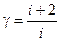(2.24)

2.6. Адиабатическое изменение объёма газа.

Наряду с изохорным, изобарным и изотермическим процессами в термодинамике часто рассматриваются процессы, протекающие в отсутствие теплообмена с окружающими телами. При адиабатическом процессе газ не обменивается теплотой с окружающей средой:

Сосуды с теплонепроницаемыми стенками называются адиабатическими оболочками, а процессы расширения или сжатия газа в таких сосудах называются адиабатическими. В адиабатическом процессе Q = 0; поэтому первый закон термодинамики принимает вид

A = –ΔU, (2.25)

т. е. газ совершает работу за счет убыли его внутренней энергии.

В термодинамике выводится уравнение адиабатического процесса для идеального газа. Это уравнение имеет вид

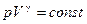(2.26)

Это соотношение называют уравнением Пуассона. Здесь 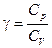– показатель адиабаты, C_p и C_V – теплоемкости газа в процессах с постоянным давлением и с постоянным объемом.

Другая форма записи уравнения Пуассона имеет вид:

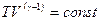, (2.27)

или

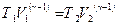, (2.28)

или

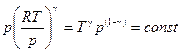. (2.29)

Для массы газа m работа при адиабатическом процессе равна

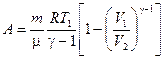(2.30)

Для одноатомного, двухатомного, многоатомного газа работа в адиабатическом процессе может быть выражена через температуры T₁ и T₂ начального и конечного состояний:

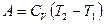(2.31)

При адиабатическом расширении газа работа меньше, чем при изотермическом расширении для данного объёма (рис. 2.3).

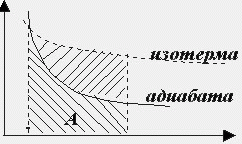
Рис. 2.3.

Адиабатический процесс также можно отнести к изопроцессам. Он (так же, как и другие изопроцессы) является процессом квазистатическим. Все промежуточные состояния газа в этом процессе близки к состояниям термодинамического равновесия

2.7. Внутренняя энергия газа Ван-дер-Ваальса

Для нахождения внутренней энергии газа Ван-дер-Ваальса, воспользуемся следующим приемом. Пусть над газом Ван-дер-Ваальса осуществляется процесс без теплообмена с окружающей средой. Тогда изменение его внутренней энергии можно записать в виде

.

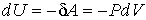(2.32)

При тех же условиях изменение внутренней энергии идеального газа можно было бы рассчитать по формуле

.

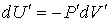(2.33)

Подстановка в эту формулу выражений (1.37) и (1.40) дает

.

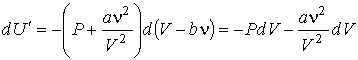(2.34)

Первое слагаемое в правой части выражения (2.34) согласно формуле (2.33) представляет собой изменение внутренней энергии газа Ван-дер-Ваальса.

Отсюда следует:

.

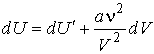(2.35)

Интегрирование этого выражения дает

.

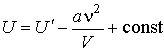(2.36)

Здесь произвольную константу интегрирования необходимо положить равной нулю, так как при 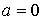выражения для внутренних энергий газа Ван-дер-Ваальса и идеального газа должна совпадать: .

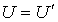Использование выражения (2.21) для внутренней энергии идеального газа позволяет записать формулу, для расчета внутренней энергии газа Ван-дер-Ваальса в виде

.

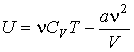(2.37)

Из выражения (2.37) следует, что внутренняя энергия газа Ван-дер-Ваальса зависит не только от его температуры, но и от объема, занимаемого им, в отличие от идеального газа. Поэтому при осуществлении изотермических процессов в газе Ван-дер-Ваальса будет изменяться его внутренняя энергия, а, следовательно, при таких процессах подведенная к газу теплота не будет равна совершенной им работе.

Внутренняя энергия идеального газа определяется кинетической энергией его молекул. В отличие от этого для газа Ван-дер-Ваальса существенное значение имеет потенциальная энергия, обусловленная силами притяжения и отталкивания.

2.8. Эффект Джоуля – Томсона.

Согласно первому началу термодинамики изменение внутренней энергии газа может быть осуществлено либо сообщением ему теплоты, либо совершением над ним механической работы. Если при адиабатическом расширении газа не совершается механическая работа, то его внутренняя энергия остается неизменной. Для идеального газа неизменность внутренней энергии эквивалентна постоянству температуры газа, что было показано в опытах Гей-Люссака.

В экспериментах, проведенных Джоулем и Томсоном на реальных газах, было установлено, что при адиабатическом расширении их температура изменяется, причем может, как повышаться, так и понижаться. Это явление получило название эффекта Джоуля-Томсона.

В опыте использовалась теплоизолированная трубка, разделенная пористой перегородкой, по обе стороны от которой находился газ (рис. 2.4).

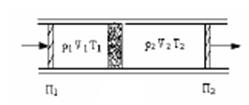
Рис. 2.4.

Газ под действием разности давлений медленно продавливался через перегородку, при помощи поршней П₁, П₂. До перегородки и после нее газ находился в термодинамически равновесных состояниях. Давление p₁, p₂ по разные стороны перегородки поддерживалось постоянным.

Исследования позволили открыть новое ранее не известное явление: если реальный газ под давлением протекает через дроссель – местное препятствие (пористую перегородку или отверстие небольшого диаметра) – то его температура изменяется. Это явление вошло в научно-техническую литературу под названием «эффект Джоуля-Томпсона».

В зависимости от начального состояния реального газа перед дросселем температура его при дросселировании может уменьшаться, увеличиваться и оставаться без изменений.

Точка, соответствующая начальному состоянию газа, при котором температура газа при адиабатическом дросселировании не изменяется, называется точкой инверсии. Температура, соответствующая этой точке, называется температурой инверсии. При температуре инверсии T_i газ при расширении не охлаждается и не нагревается.

При начальных температурах газа, которые меньше температуры инверсии, реальный газ при дросселировании будет охлаждаться, а при начальных температурах больше температуры инверсии - нагреваться. Объясняется этот эффект тем, что в силу закона сохранения энергии, уменьшение кинетической энергии реального газа равно приращению его потенциальной энергии. Если потенциальная энергия взаимодействия молекул реального газа при расширении возрастает, то его температура при этом падает. Если потенциальная энергия уменьшается, то его температура растет. В частности, для газа Ван-дер-Ваальса, если силы притяжения играют более существенную роль, чем силы отталкивания, то газ при расширении охлаждается, а если силы отталкивания превосходят силы притяжения, то его температура увеличивается.

Большинство газов, за исключением водорода и гелия, имеет довольно высокую температуру инверсии (600°С и выше), поэтому практически для всех газообразных веществ в области, близкой к критической, адиабатическое дросселирование приводит к понижению температуры.

Дайверам хорошо знаком эффект охлаждения газа при расширении. Именно этот эффект "повинен" в обмерзании регуляторов. При расширении воздуха (смесь азота, кислорода, углекислого газа и так далее) и перепаде давления по обе стороны дросселирующей перегородки 196 бар (бар – (греч. βάρος – тяжесть) – внесистемная единица измерения давления, равная 10⁵ Н/м², то есть приблизительно равная давлению атмосферы), и начальной температуре 17°С температура газа снизиться на 35 градусов. Такого перепада температур достаточно, чтобы частицы влаги, плохо отфильтрованные в компрессоре, замерзли. Кристаллики льда покрывают внутренние механизмы регулятора, блокируя их.

2.9. Тепловая машина. Холодильная машина. КПД.

Создание и развитие термодинамики было вызвано, прежде всего, необходимостью описания работы и расчета тепловых машин. Первыми тепловыми машинами были паровые двигатели, замкнутый термодинамический цикл которых впервые был описан в 1690 году английским физиком Дени Папином (1647-1712). Первые тепловые двигатели предназначались для подъема воды из шахт и были изобретены английскими инженерами в 1698 году Томасом Севери (1650 - 1715) и в 1712 году Томасом Ньюкоменом (1663 - 1715). Если в насосе Севери использовался пар в качестве тела, непосредственно толкающего воду, то машина Ньюкомена была первой поршневой паровой машиной. Отметим, что идея использования поршня принадлежит Папину.

Широкое применение паровых машин в промышленности началось после изобретения в 1774 году Джеймсом Уаттом (1736 - 1819) паровой машины, в которой работа совершалась без использования атмосферного давления, что значительно сократило расход топлива. Уатт дополнил свои машины важнейшими механическими изобретениями, такими как преобразователь поступательного движения во вращательное, центробежный регулятор, маховое колесо и т.д. В 1784 году Уатт запатентовал универсальную паровую машину двойного действия, в которой пар совершал работу по обе стороны поршня.

Сейчас разработано большое количество разнообразных тепловых машин, в которых реализованы различные термодинамические циклы. Тепловыми машинами являются двигатели внутреннего сгорания, реактивные двигатели, различные тепловые турбины и т.д.

В основе работы тепловой машины лежит замкнутый термодинамический процесс или цикл.

Круговым процессом (или циклом) называется такой процесс, в результате которого термодинамическая система, претерпев ряд изменений, возвращается в исходное состояние. Круговой процесс может быть равновесным или неравновесным.

Всякий равновесный процесс представляет непрерывную последовательность равновесных состояний термодинамической системы. Равновесные состояния – это такие состояния, в которых все параметры системы имеют определенные значения и остаются постоянными до тех пор, пока не изменятся внешние условия. В равновесном процессе внешние условия изменяются настолько медленно, что термодинамическая система успевает прийти в равновесие с окружающей средой. Всякий равновесный процесс является обратимым: термодинамическую систему можно вернуть из конечного состояния в начальное. При этом во внешней среде не произойдет никаких изменений. Это означает, что в обратном процессе система пройдет через те же состояния, через которые она проходила в прямом процессе.

Тепловой машиной называется любое периодически действующее устройство, которое производит работу за счет получаемой извне теплоты. Прямым круговым процессом (циклом тепловой машины) называется цикл, в котором полученная извне теплота превращается в полезную работу. Обратным круговым процессом (циклом холодильной машины) называется цикл, в котором полученная извне работа затрачивается на перенос теплоты от менее нагретых тел к более нагретым телам.

Если тело (термодинамическая система) производит работу за счет внутренней энергии теплого резервуара, то его называют рабочим телом тепловой машины или просто рабочим телом. Система может состоять из одного рабочего тела.

Модель простейшей тепловой машины: идеальный газ, заключенный в вертикальном цилиндре с подвижным поршнем. Если на поршень поставить груз и нагревать газ в цилиндре, то в результате нагревания газ расширяется и совершает полезную работу по поднятию груза (газ получает теплоту Q₁). Если груз убрать и прекратить нагревание газа, то газ отдает тепло в окружающую среду (газ отдает теплоту Q₂) и его объём уменьшается. Среда исполняет роль холодильника. Поршень вернется в начальное состояние (рис. 2.5).

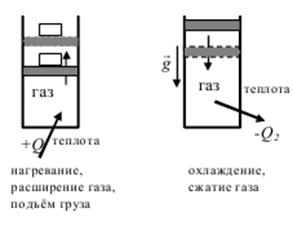
Рис. 2.5. Модель тепловой машины.

Таким образом, схема тепловой машины состоит из нагревателя (горячее тело), холодильника (холодное тело), рабочего тела (газ) (рис. 2.6).

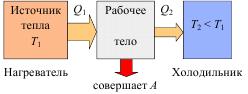
Рис. 2.6. Схема тепловой машины.

От нагревателя отбирается теплота Q1, которая расходуется на совершение работы А, холодильнику передаётся теплота Q2. Отметим, что наличие холодильника и передача ему части полученной от нагревателя теплоты, является обязательным, так как иначе работа тепловой машины невозможна. Действительно, для получения механической работы необходимо наличие потока, в данном случае потока теплоты. Если же холодильник будет отсутствовать, то рабочее тело неизбежно придет в тепловое равновесие с нагревателем, и поток теплоты прекратится. В качестве холодильника выступает окружающая среда.

Графическим представлением циклов тепловой машины и холодильной машины в координатах P, V являются замкнутые линии (рис. 2.7).

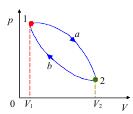
Рис. 2.7. Прямой цикл протекает по часовой стрелке.

Если при совершении цикла обход замкнутой линии осуществляется по часовой стрелке, то полезная работа А цикла положительная. В этом случае это цикл тепловой машины (рис. 2.7). А за цикл > 0; работа А равна разности площадей фигурт, ограниченных ординатами V₁, V₂ и линиями 1-a-2 и 2-b-1

Рассмотрим произвольный круговой прямой цикл. Пусть рабочее тело перешло из состояния 1 в состояние 2 по кривой 1а2. Рабочим телом является идеальный газ. Значит, идеальный газ расширился, его объем изменился от V₁ до V₂. Газ совершил положительную работу А₁. Процесс 1а2: Q₁ = U₂ − U₁ + A₁ – первое начало термодинамики. Работа А₁ равна площади под кривой 1a2.

Вернем газ в исходное состояние (в состояние 1). Для этого газ нужно сжать, то есть совершить работу над газом. Пусть сжатие газа происходит по кривой 2б1 (направление процесса указано стрелкой). Обозначим А₂ – работа, которая совершается при сжатии газа. Если внешние силы совершают работу над системой, то работа считается отрицательной. Следовательно, А₂ < 0. Графически А₂ выражается площадью под кривой 2б1.

Рабочее тело вернулось в исходное состояние. Система совершила цикл. Полезная работа А графически выражается площадью петли 1-а-2-б-1.

Суммарная (полезная) работа, совершенная в результате этого цикла равна разности площадей: площадь под кривой 1-а-2 минус площадь под кривой 2-б-1 или А₁ – А₂. Таким образом,

A = A₁ + (−A₂) = A₁ − A₂. (2.38)

Коэффициент полезного действия тепловой машины (КПД) равен отношению произведенной машиной за цикл полезной работы А к полученной извне теплоте Q1:

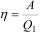(2.39)

Применим к циклу тепловой машины первое начало термодинамики: Q = ΔU + A, где Q – полученное рабочим телом количество теплоты за цикл, ΔU – приращение внутренней энергии рабочего тела за цикл. Так как внутренняя энергия является функцией состояния, её приращение за цикл равно нулю: ΔU = 0. Величина Q – алгебраическая сумма теплоты, полученная рабочим телом за цикл, в процессах нагревания и охлаждения. Тогда Q = Q₁ – Q₂.

Q =ΔU + A, так как ΔU = 0, то Q = A = Q₁ − Q₂.

Коэффициент полезного действия, сокращенно, КПД тепловой машины η – это отношение работы к количеству теплоты, полученной от нагревателя.

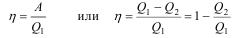. (2.40)

Так как Q₂ < Q₁, то КПД тепловой машины всегда меньше единицы. Отсюда вывод, что тепло нельзя превратить в работу без необратимых потерь.

Холодильная машина.Термодинамический цикл, осуществляемый в обратном направлении, может быть использован для работы холодильной машины, схема и термодинамический цикл которой приведены соответственно на рис. 2.7. Такие машины, в отличие от тепловых двигателей, предназначены не для получения механической работы из теплоты, а позволяют осуществлять охлаждение различных тел за счет совершения работы.

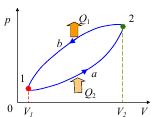а б

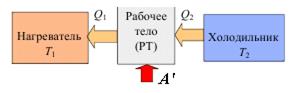
Рис. 2.7. Схема холодильной машины (а). Обратный термодинамический цикл работы (б).

На рис. 2.7, а – Q₂ – тепло отнятое от холодного тела. Q₁ – тепло переданное нагревателю (более горячему телу). А’ = Q₂ – Q₁ – работа, затрачиваемая на передачу тепла от более холодного к более горячему телу.

На рис. 2.7, б – линия 1-a-2 – расширение рабочего тела с поглощением теплоты Q₂; линия 2-b-1 – сжатие рабочего тела с передачей нагревателю теплоты Q_1.

В холодильной машине за счет совершения внешними телами работы 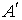над рабочим телом происходит отвод теплоты Q₂ от охлаждаемого тела и передача теплоты Q₁ тепловому резервуару, в качестве которого обычно выступает окружающая среда.

Коэффициент полезного действия или холодильный коэффициент холодильной машины можно определить как отношение отнятой от охлаждаемого тела теплоты 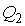к затраченной для этого механической работе :

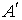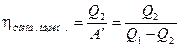(2.41)

Так как в зависимости от конкретной конструкции холодильной машины количество отводимой от охлаждаемого тела теплоты 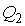может, как превышать затраченную работу 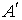, так и быть меньше ее, то К.П.Д. холодильной машины, в отличие от К.П.Д. тепловой машины, может быть как больше, так и меньше единицы.

Холодильная машина может быть использована не только для охлаждения различных тел, но и для отопления помещения. Действительно, даже обычный бытовой холодильник, охлаждая помещенные в нем продукты, одновременно нагревает воздух в комнате. Принцип динамического отопления был предложен Томсоном (лордом Кельвином) и положен в основу действия современных тепловых насосов. Этот принцип заключается в использовании обращенного цикла тепловой машины для перекачки теплоты из окружающей среды в помещение.

Схема теплового насоса совпадает с приведенной на рис. 2.7 схемой холодильной машины. Основное отличие заключается в том, что теплота Q₁ подводится к нагреваемому телу, например к воздуху в обогреваемом помещении, а теплота Q₂ забирается из менее нагретой окружающей среды. Термодинамические циклы холодильной машины и теплового насоса совпадают (см. рис. 2.7).

К.п.д. теплового насоса определяется как отношение полученной нагреваемым телом теплоты Q₁ к затраченной для этого механической работе :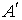

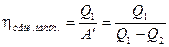(2.42)

Учитывая то, что отводимая от окружающей среды теплота 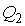всегда отлична от нуля, К.П.Д. теплового насоса, в соответствии с его определением, обязательно должен быть больше единицы. Из сравнения формул (2.39) и (2.42) следует, что К.П.Д. теплового насоса является величиной, обратной К.П.Д. тепловой машины:

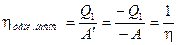. (2.43)

К.П.Д. теплового насоса тем выше, чем больше теплоты 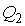отводится от окружающей среды. Указанный результат не противоречит законам термодинамики, так как в данном случае для перекачки теплоты от менее нагретой окружающей среды к более нагретому воздуху в помещении используется работа внешних сил. При этом на каких-то участках цикла рабочее тело может совершать положительную работу, так как при тепловом контакте с окружающей средой его температура должна быть ниже температуры среды.

2.10. Цикл Карно. Идеальная тепловая машина

В природе и технике существует бесконечное количество циклов. Но тогда возникает вопрос, какой цикл из всех существующих циклов является самым экономичным, т.е. какой цикл имеет наибольший коэффициент полезного действия (КПД)? Такой цикл был предложен французским инженером Карно в 1824 г.

Циклом Карно называется цикл тепловой машины, которая связана только с двумя тепловыми резервуарами: нагревателем и холодильником. В качестве рабочего тела используется идеальный газ. Цикл Карно состоит из двух равновесных изотермических процессов и двух равновесных адиабатических процессов. Тепловую машину, работающую по циклу Карно, называют машиной Карно или идеальной тепловой машиной.

Обратимый цикл Карно состоит из двух изотерм, описывающих процесс теплопередачи от нагревателя к рабочему телу и от рабочего тела к холодильнику, и двух адиабат, описывающих расширение и сжатие рабочего тела в тепловой машине (см. рис. 2.8). Температура нагревателя считается равной 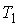, а температура холодильника - соответственно 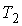. При этом температуры нагревателя 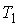и холодильника 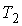постоянны, что должно обеспечиваться бесконечно большой теплоемкостью используемых тепловых резервуаров. При первом изотермическом процессе 1-2 происходит передача рабочему телу теплоты 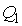, причем эта теплота передается бесконечно медленно, при практически нулевой разнице температуры между нагревателем и рабочим телом. Далее рабочее тело подвергается адиабатическому расширению без теплообмена с окружающей средой (процесс 2-3). При последующем изотермическом процессе 3-4 холодильник забирает у рабочего тела теплоту 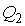. Процесс 4-1 представляет собой адиабатическое сжатие, переводящее рабочее тело в первоначальное состояние.

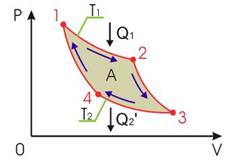
Рис. 2.8. Термодинамический цикл Карно

Французский ученый Сади Карно показал, что максимально возможное значение КПД тепловой машины равно

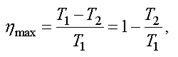(2.44)

где T₁ - температура нагревателя, T₂ - температура холодильника.

Из сравнения уравнений (2.40) и (2.44) следует, что 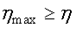или 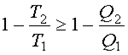. Отсюда

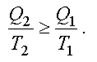(2.45)

На основании этого неравенства можно прийти к понятию энтропия и второму началу термодинамики.

Повышение КПД тепловых двигателей и приближение его к максимально возможному значению - важнейшая техническая задача. Однако, все тепловые двигатели выделяют большое количество теплоты, что называется тепловым загрязнением, и выбрасывают в атмосферу вредные для растений и животных химические соединения. Это ставит серьезные проблемы охраны окружающей среды.

2.11. Второе начало термодинамики. Энтропия.

Первый закон термодинамики, являясь частным случаем всеобщего закона о сохранении и превращении энергии, разрешает проведение любого процесса, не устанавливая условий, при которых возможен этот процесс. Он не решает вопроса о том, будет ли теплота передаваться от горячего тела к холодному или наоборот. Этот вопрос решает второй закон, выделяя из всех воображаемых процессов только те, которые в действительности могут произойти.

Следует отметить, что второй закон не ограничивается рамками техники, его действие распространяется на химию, биологию, астрономию, социологию и даже на явление жизни

Второе начало термодинамики является фундаментальным законом природы. Оно охватывает самый широкий круг природных явлений и указывает направление, в котором самопроизвольно протекают термодинамические процессы.

Второе начало термодинамики устанавливает наличие в природе фундаментальной асимметрии, т.е. однонаправленности всех происходящих в ней самопроизвольных процессов. Об этой асимметрии свидетельствует всё окружающее нас: горячие тела с течением времени охлаждаются, однако холодные сами по себе никогда не становятся горячими; прыгающий мяч в конце концов останавливается, но покоящийся мяч самопроизвольно не начинает подскакивать. Здесь проявляется свойство природы, отличное от свойства сохранения энергии. Это свойство состоит в том, что, хотя баланс энергии должен сохраняться в любом процессе, распределение имеющейся энергии изменяется необратимым образом. Второе начало термодинамики указывает естественное направление, в котором происходит изменение распределения энергии, причем это направление не зависит от её общего количества.

Смысл второго начала заключается в том, что любая система, предоставленная самой себе, стремится к одному вполне определённому состоянию – состоянию равновесия с окружающей средой. Такое состояние имеет минимум энергии.

Второе начало термодинамики, как и первое, имеет несколько формулировок.

В наиболее общей формулировке второе начало термодинамики предложеноЛ. Больцманом: природа стремится к переходу от менее вероятных состояний к более вероятным.

Невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, полностью в работу.

Невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.

Эти формулировки показывают, что тепловые процессы являются необратимыми. Мерой необратимости процесса, мерой хаотичности является энтропия.

К определению энтропии S можно прийти на основе анализа работы тепловых машин. Если система получает тепло 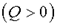или отдает тепло 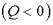, то состояние ее меняется. Тогда, при изменении состояния системы, можно найти не саму энтропию, а только ее изменение, т. е.

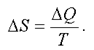(2.46)

Для тепловой машины изменение энтропии нагревателя и холодильника равны:

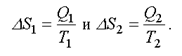(2.47)

Формула 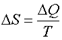справедлива для изотермического процесса и представляет собой термодинамическое определение энтропии. Энтропией называется термодинамическая величина, изменение которой в системе пропорционально изменению ее тепловой энергии, деленной на абсолютную температуру. Для любого процесса можно найти бесконечно малое изменение энтропии, т. е. ее дифференциал

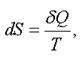(2.48)

где 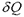- элементарная теплота (см. формулу (2.8)).

В интегральной форме для любого процесса изменение энтропии равно

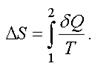(2.49)

Найдем изменение энтропии за один цикл для тепловой машины. Из неравенства (2.45) следует, что 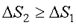. Полное изменение энтропии за цикл больше или равно нулю

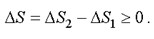(2.50)

Знак равенства ΔS = 0 относится к обратимым процессам, которые являются бесконечно медленными процессами.

Знак неравенства ΔS > 0 относится к необратимым процессам. В реальных системах все процессы необратимы. Например, расширение газа, выравнивание температуры.

Таким образом, второе начало термодинамики формулируется и как закон возрастания энтропии (2.50).

Во всех необратимых процессах в замкнутой системе энтропия всегда возрастает.

Возрастание энтропии сопровождается выравниванием температуры или плотности газа. Это можно связать с порядком и беспорядком. Под порядком будем понимать сосредоточение частиц или энергии в определенном месте пространства, а под беспорядком (хаосом) - равномерное распределение их во всем объеме. Тогда возрастание энтропии при совершающихся без внешних воздействий необратимых процессах отражает природное стремление систем переходить от состояния, более упорядоченного в состояние менее упорядоченное. Этот процесс сопровождается рассеянием (или диссипацией) энергии.

Как мы видим, второе начало термодинамики определяет направленность тепловых процессов в изолированных системах, они всегда протекают в сторону роста энтропии, в сторону увеличения беспорядка. Капелька туши растворяется во всем объеме, колечко сигаретного дыма тает, огонь костра гаснет, разрушаются горы, гаснут звезды и т. д. Вся практическая деятельность людей как в технике, так и в сельском хозяйстве, представляет собой не что иное, как создание из природных материалов искусственных структур, т. е. в том или ином смысле борьбу с самопроизвольным ростом энтропии.

Возникновение упорядоченных структур возможно только в незамкнутых, т. е. в открытых системах. Открытой системой называется система, которая обменивается энергией и веществом с окружающей средой. В открытых системах энтропия может как возрастать, так и убывать в зависимости от знака .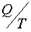

Трудами Ильи Пригожина (датский физик русского происхождения) строго доказано, что в открытых системах, находящихся в неравновесном состоянии, при определенных условиях из хаоса может возникать порядок. Процесс возникновения из хаоса упорядоченных структур называется самоорганизацией. Процессы самоорганизации являются общими для живой и неживой природы.

Феномен жизни является примером сохранения и увеличения упорядоченности и, следовательно, уменьшения энтропии. Жизненный цикл наблюдается только в открытых системах. Он включает в себя три стадии: рождение, развитие, смерть. На первых двух стадиях энтропия понижается, возникает и развивается структура. На этих стадиях живой организм поддерживает связь с окружающей средой. На третьей стадии система становится замкнутой, энтропия возрастает и достигает максимума. В этом смысле жизнь - это борьба с возрастанием энтропии. Человек существует, пока он активно поддерживает связь с окружающим миром, обменивается с ним энергией, веществом и информацией.

Заключение:

1. Второй закон термодинамики объясняет направление протекания процессов и вводит понятие энтропии ΔS=Q/T. Критерием самопроизвольного протекания процесса в

изолированной системе является ΔS>0, равновесия – ΔS=0.

2. Энтропия является функцией состояния и ее смысл расшифровывается в статистической термодинамики как мера беспорядка системы. Чем больше беспорядок, тем больше энтропия.